Распределение Пуассона

Опр. С.в. Х имеет распределение Пуассона, если возможные значения: 0,1,2,…,m,…,¥ (бесконечное, но счётное множество значений), а соответствующие вероятности выражаются формулой:

(m = 0,1,2,…)

Распределение Пуассона играет большую роль в практическом применении теории вероятности: многие физические явления приводят к именно такому распределению.

Теорема параметра а:

Параметр а в законе Пуассона является одновременно мат. ожиданием и дисперсией с. в. Х, распределённой по закону Пуассона.

Док-во:

Ряд Тейлора: 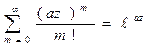Þ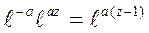

Мат. ожидания:

Þ M_x= a

;

Второй начальный момент:

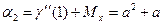
Дисперсия:

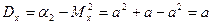Þ

Среднее квадратичное отклонение:

Теорема: Закон Пуассона является предельным для биноминального распределения при стремлении числа опытов n к бесконечности и стремлении параметра p к нулю, но так, что

Док-во:

Мат. ожидание M_x = np = a Þ

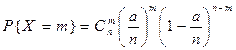
е^-а

Преобразуем выражение, стоящее под знаком предела: //

где , ,

а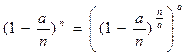при n ® ¥ скобка ® е^-аÞ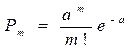

Замечание:

Распределение Пуассона с параметром a=np можно приближенно применять вместо биноминального, когда число опытов n очень велико, а число p очень мало.

Пример: включение – выключение выключателя.

Рассмотрим задачу:

Пусть на оси времени ot случайным образом возникают точки – моменты появления каких – то однородных событий (например, вызов на телефонной станции, приход посетителей в магазин и т. д.)

Опр. Последовательность таких моментов обычно называют потоком событий.

1. Опр. Стационарность – это свойство означает, что вероятность попадания того или иного числа событий на участок времени длины t не зависит от того, где на оси ot находится этот участок, а зависит только от его длины t.

Опр. Интенсивность потока - это среднее число событий, появляющихся в единицу времени l (для стационарного потока l=const)

2. Опр. Ординарность – это свойство выражается в том, что вероятность попадания на малый участок Dt двух или более событий пренебрежительно мала по сравнению с вероятностью попадания на него одного события.

, где n_соб. Число попаданий на отрезке Dt

3. Опр. Отсутствие последствий - это свойство означает, что вероятность попадания того или иного числа событий на заданный участок оси ot не зависит от того, сколько событий попало на любой другой, не пересекающийся с ним участок (в частности «будущее» потока не зависит от его прошлого).

Опр. Простейшим (или стационарным, пуассоновским ) потоком называется поток событий, обладающий свойствами: стационарностью, ординарностью и отсутствием последствий.

Возьмём на оси ot участок времени t. Разделим мысленно участок t на n равных частей длины Dt = t/ n.

M_xDt = lDt

При очень больших n, учитывая ординарность потока, вероятностью попадания двух событий на участок Dt можно пренебречь.

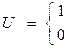При U =1, Dt – занят; при U = 0, Dt – пуст.

M [ U ] = p Dt

c другой стороны: M [ U ] = l Dt

Þ 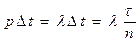- вероятность того, что Dt занято.

Из свойства «без последствий» Þ независимость всех участков.

количество занятых ячеек

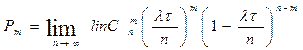
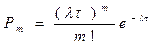
Замечание:

Для простого потока событий через интервал времени t, вероятность, что за это время произойдёт m событий: .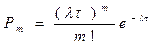

Если закон не удовлетворяет условию стационарности, то в законе Пуассона:

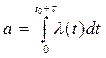
Замечание:

Ось ot необязательно должна быть осью с координатами времени, координаты могут иметь любой физический смысл (например, пространства)

Опр. Интенсивность потока – это среднее число событий на единицу измерения пространства.

Тогда: l=f (координаты пространства)

а: а=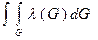

Пример:

На автоматическую телефонную станцию поступает простейший поток вызовов с интенсивностью l=0.8 вызов минута.

Найти вероятность того, что за две минуты:

а) не придёт ни одного вызова

б) придёт ровно один вызов

в) придёт хотя бы один вызов

Решение:

Х – число вызовов за 2 минуты

а= lt = 2*0,8=1,6

а) P₀ = а⁰ / 0! * е^-1,6 = е^-1,6 = 0,202

б) Р₁ = а¹ / 1! * е^-1,6 = 1,6*е^-1,6 =0,323

в) Р{X ³ 1 } = 1- P₀ =1- 0.202 = 0.798

Дата добавления: 2014-01-14