Условные числовые характеристики системы случайных величин (Х,У). Регрессия

Опр. Условным математическим ожиданием одной из с.в, входящих в систему (Х,У), называется её мат. ожидание, вычисленное при условии, что другая с.в. приняла определенное значение, т.е. найденное на основе условного закона распределения.

Для двух дискретных с.в.:

где p_{yj | xi}=P{Y=y_j| X=x_i}

p_{xi | yj}=P{X=x_i| Y=y_j}

Для двух непрерывных с.в.:

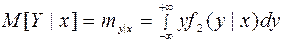
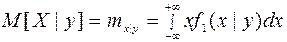
Опр. Условное мат. ожидание с.в. У при заданном Х=х: M[Y|x]=M_y|x называется регрессией У на х. Графики этих зависимостей от х и у называются линиями регрессии.

Пример:

Матрица распределения системы двух с.в. (Х,У) задана таблица:

(Х,У):	xi | yj
		0.1		0.2
		0.3
	0.1	0.3

1) Найти числовые характеристики системы (Х,У):

M_x, M_y, D_x, D_y, s_x, s_y, K_xy, r_xy

2) Построить линии регрессии У на Х и Х на У соответственно.

Решение: 1) Ряды отдельных величин:

P_x1=P{X=1}=0.1+0.2=0.3

P_x2=P{X=2}=0.3

P_x3=P{X=4}=0.1+0.3=0.4

X:

0,3	0,3	0,4

М_х=1*0,3+2*0,3+4*0,4=2,5

a₂[X]=1²*0,3+2²*0,3+4²*0,4=7,9

D_x=a₂[X]- М_х=1.65

s_x=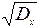=1.285

P_y1=P{Y=0}=0.1+0.1=0.2

P_y2=P{Y=2}=0.3+0.3=0.6

P_y3=P{Y=5}=0.2

Y:
0.2	0.6	0.2

M_y=2*0.6+5*0.2=2.2

a₂[X]=2²*0.6+5²*0.2=7.4

D_y=a₂[Y]- М_y=7.4-(2.2)²=2.56

s_x=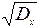=1.6

M[XY]=2*2*0.3+2*4*0.3+1*5*0.2=4.6

K_xy=4.6-2.5*2.2=-0.9

Между Х и У существует отрицательная линейная зависимость, т.е. при увеличении одной из них другая имеет некоторую тенденцию уменьшаться.

2)

P_y1|x1=P{Y=0|X=1}=0.1/0.3=1/3

P_y2|x1=P{Y=2|X=1}=0/0.3=0

P_y3|x1=P{Y=5|X=1}=0.2/0.3=2/3

à M_y|x1=5*2/3=10/3

P_y1|x2=0 P_y2|x2=1 P_y3|x2=0 M_y|x2=2

P_y1|x3=1/4 P_y2|x3=3/4 P_y3|x3=0 M_y|x3=3/2

Также

P_х1|у1=1/2 P_х2|у1=0 P_х3|у1=1/2 М_х|у1=2,5

P_х1|у2=0 P_х2|у2=1/2 P_х3|у2=1/2 М_х|у2=3

P_х1|у3=10 P_х2|у3=0 P_х3|у3=0 М_х|у3=2

Дата добавления: 2014-01-14