Распределение средней арифметической для выборок из нормальной совокупности. Распределение Стьюдента

Теорема 2.4 Если случайная величина Х подчиняется нормальному закону распределения с параметрами 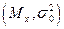, а 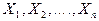- ряд независимых наблюдений над случайной величиной Х, каждое из которых имеет те же числовые характеристики, что и Х, т.е.

,.....,=

,.....,=

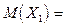
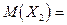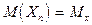
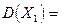
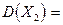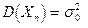
то выборочная средняя 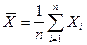также подчиняется нормальному закону распределения.

В литературе по статистике приводится таблица нормального распределения с параметрами (0, 1), т.е. 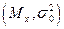, в нашем случае параметры равны:

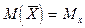
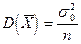
Поэтому нам необходимо найти связь между нашим распределением и табличным, т.е. нам нужно знать как выражается наша случайная величина через случайную величину подчиняющуюся табличному распределению.

Нормированное отклонение подчиняется нормальному закону распределения.

M () =

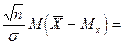
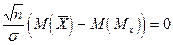
D()=

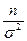
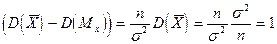
Пример Автомат штампует детали. Контролируется длина детали, которая подчиняется нормальному закону распределения. Найти вероятность того, что средняя длина деталей, отобранных случайным образом, отклонится от математического ожидания более, чем на 2 мм, если дисперсия случайной величины Х равна 9 кв. мм, а количество деталей в выборке n=16.

Решение

Т.к. детали отбираются независимо друг от друга, то случайная величина 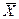имеет нормальное распределение с мат. ожиданием 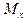и дисперсией 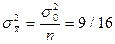кв.мм

Теперь найдем вероятность того, что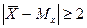

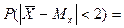
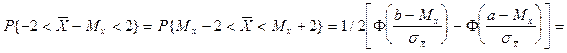
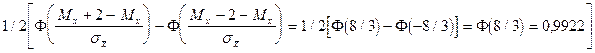
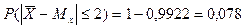
Итак, если случайная величина Х подчиняется нормальному закону распределения, то нормированное отклонение 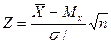также подчиняется этому закону.

Однако дисперсия почти всегда оказывается неизвестной.

Большой практический интерес имеет распределение Стьюдента.

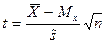
где 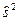-несмещенная и состоятельная оценка дисперсии, вычисленная по выборочным данным.

В литературе по мат. статистике доказывается, что дифференциальная функция t - распределения Стьюдента имеет вид ,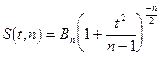

где 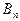- коэффициент, зависящий только от объёма n

t - текущая переменная

n - величина объёма

Для этой функции составлены таблицы

Из анализа табличных данных видно, что уже при n=50 распределение Стьюдента мало отличается от нормального.

Дата добавления: 2014-01-14