Понятие доверительного интервала. Доверительная вероятность

В 2.3 были рассмотрены некоторые выборочные характеристики, которые лучше всего в смысле несмещенности, эффективности и состоятельности оценивали параметры распределения генеральной совокупности.

Опр. Оценка неизвестного параметра генеральной совокупности одним числом называется точечной оценкой.

Наряду с точечным оцениванием, статистическая теория оценивания параметров занимается вопросами интервального оценивания.

Опр. Доверительным интервалом 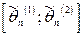для параметра 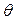называется такой интервал, относительно которого можно с заранее выбранной вероятностью 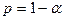, близкой к единице,утверждать, что он содержит неизвестное значение параметра 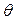, т.е.

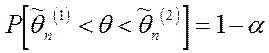
Вероятность 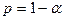принято называть доверительной вероятностью.

Замечание: Выбор доверительной вероятности не является математической задачей, а определяется условиями конкретно решаемой задачи.

9.8 Построение доверительного интервала для математического ожидания при известной .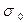

Случайная величина Х распределена нормально

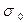- известно

Требуется оценить неизвестное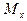

Наилучшей оценкой для этого является выборочная средняя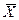

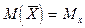
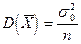
нормированное отклонение 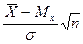распределено нормально с M[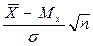]=0 и

Вероятность любого отклонения 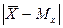может быть вычислено по формуле

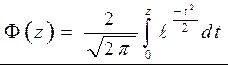табличный интеграл

Далее преобразовываем формулу:

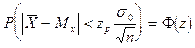
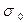( известно, требуется оценить неизвестное )

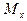Перепишем в виде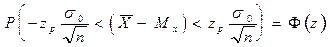

è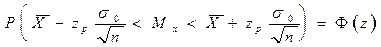

Вывод: С вероятностью Ф(z) интервал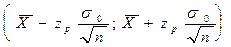

является доверительным интервалом для оценки .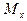

9.9 Построение доверительного интервала для математического ожидания при неизвестной .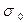

Случайная величина Х распределена нормально

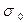неизвестно

Требуется оценить неизвестное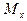

Величина 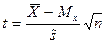распределена по закону Стьюдента

Выбираем p=1-, зная объём выборки. Из таблицы для 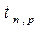получаем значение

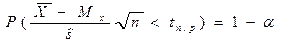
è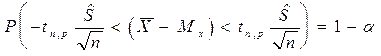

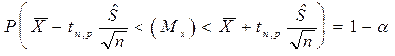
Вывод: С вероятностью (надёжностью) p=1-можно утверждать, что интервал 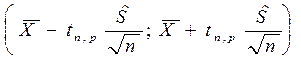является доверительным для оценки мат. ожидания.

Замечание: 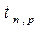зависит не только от требуемой вероятности, но и от объёма выборки.

Дата добавления: 2014-01-14