Дисперсионный анализ с неравным числом наблюдений в ячейке

В матрице наблюдений может оказаться неодинаковое количество наблюдений в ячейках, а некоторые ячейки вообще могут быть пустыми.

Текстильная фабрика:

Качество сырья в партиях - фактор А (I, II, III)

Состояние машин - фактор В (1, 2, 3, 4, 5)

I	х111, х112, х113, х114, х115 (1,1)	х121, х122, х123, х124, х125 (1,2)	--\-- (1,3)	--\-- (1,4)	--\-- (1,5)
II	х211, х212, х213, х214, х215 (2,1)	х221, х222, х223, х224, х225 (2,2)	--\-- (2,3)	--\-- (2,4)	--\-- (2,5)
III	х311, х312, х313, х314, х315 (3,1)	--\-- (3,2)	--\-- (3,3)	--\-- (3,4)	х351, х352, х353, х354, х355 (3,5)

Вторая машина испортилась при обработке первой партии.

Третья машина останавливалась.

Получилось:

I	х111, х112, х113, х114, х115 (1,1)	(1,2)	х131, х132, х133 (1,3)	х141, х142, х143, х144, х145 (1,4)	х151, х152, х153, х154, х155 (1,5)
II	х211, х212, х213, х214, х215 (2,1)	х221, х222, х223, х224, х225 (2,2)	х231, х232, х233, х234, х235 (2,3)	х241, х242, х243 (2,4)	(2,5)
III	х311, х312, х313, х314, х315 (3,1)	х321, х322, х323, х324, х325 (3,2)	х331, х332, х333 (3,3)	х341, х342, (3,4)	х351, х352, (3,5)

Предыдущая схема анализа не подходит.

Представим каждое наблюдение х_ijk в виде:

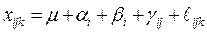
i=1,2,…….., I – количество строк

j=1,2,……..,J – количество столбцов

k=1,2,…….,K – количество наблюдений в ячейке

m - среднее всего комплекса

a_i – эффект, обусловленный действием фактора А

b_i - эффект, обусловленный действием фактора В

g_ij - эффект, обусловленный взаимодействием факторов А и В

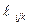- вариация результатов внутри отдельной ячейки.

С помощью 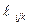учитываются все неконтролируемые факторы.

На составляющие 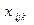накладывается ряд ограничений

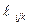{} - нормально распределена с М_е=0 и s_е²=s²

Средние эффекты факторов А и В и их взаимодействия предполагаются равными нулю, т.е.

Если в матрице есть пустые клетки, то простых формул привести нельзя.

Начинаем с проверки на взаимодействие.

Если взаимодействие значительно, то считается, что влияние факторов А и В доказано.

Н_АВ – гипотеза об отсутствии влияния взаимодействия А и В.

Далее, если взаимодействие А и В незначительно, то переходим к проверке влияния на результирующий признак каждого из факторов А и В по схеме однофакторного дисперсионного анализа.

Проверка гипотезы Н_АВ.

1. Вычисляем сумму квадратов отклонений каждого отклонения от своего среднего.

Q_е - характеризует вариацию наблюдений, которая вызвана неконтролируемыми факторами.

M(e_ij) =0èx_ij*=M_x+a_i+b_j+g_ij è x_ij*=(M_x+a_i+b_j+g_ij+е_ijk)-(M_x+a_i+b_j+g_ij)= е_ijk

è Q_е=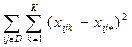

D- множество заполненных ячеек

Q_е – имеет k=(n-p) степеней свободы

n – общее количество наблюдений

p – количество заполненных ячеек

2. Если взаимодействие факторов незначимо, то среднюю ячейки можно представить в следующем виде:

x_ij*=M_x+a_i+b_j

Тогда х_ijk-х_ij*=(M_x+a_i+b_j+g_ij+е_ijk)-(M_x+a_i+b_j)= (g_ij+е_ijk)

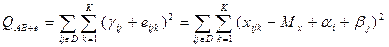
Q_АВ+е – Q_е – характеризует взаимодействие А и В

k= (P – I – J + 1)

3.

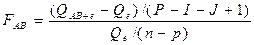
F_a, k_AB, k_e? F_AB

Эта система имеет единственное решение:

Осталось решить её и рассчитать Q_АВ+е

Допустимое количество пустых ячеек:

Условия:

1. k₁= (P – I – J + 1) и k₂=(n-p)¹0

2. Система имеет единственное решение.

Замечание:

При невыполнении хотя бы одного из этих условий задача не может быть решена.

Пример:

	В1	В2	В3
А1	0,5; 0,6	---	0,4; 0,3
А2	0,6; 0,6	0,2; 0,6; 0,4	0,6; 0,5

4. Для того, чтобы вычислить Q_АВ+е, необходимо найти оценки M_x, a_i, b_j, лучше воспользоваться методом наименьших квадратов.

Т.е. минимизируется статистика 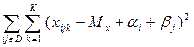a по каждому из параметров M_x, a_i, b_j.

Т.е.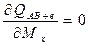

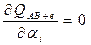
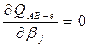
G_i – количество элементов в i-ой строке

Н_j – количество элементов в j-ом столбце

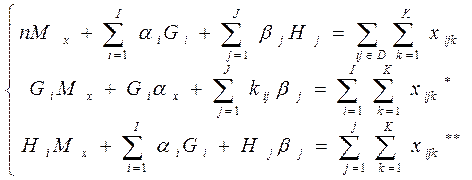
Система имеет I+J+1 уравнений и I+J+1 неизвестных.

Однако среди уравнений лишь I+J-1 линейно независимы;

Сумма уравнений второй и третьей групп равна первому уравнению.

èРешение системы не является единственным.

Учитывая 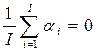и 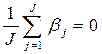, исключаем два уравнения, например, первое и последнее.

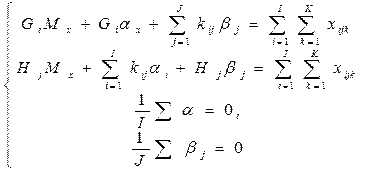
Эта система имеет единственное решение.

Осталось решить её и рассчитать Q_AB+e.

Допустимое количество пустых ячеек:

Условия:

1. k₁ = (p – I – J + 1) 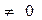и k₂=(n – p) .

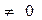2. Система имеет единственное решение.

Замечание: При невыполнении хотя бы одного из этих условий задача не может быть решена.

Пример:

Рассмотрим двухфакторный комплекс.

Матрица наблюдений имеет следующий вид:

В	В1	В2	В3
А
А1	0,5; 0,6	----	0,4; 0,3
А2	0,6; 0,6	0,2; 0,6; 0,4	0,6; 0,5

Для удобства вычисления составим вспомогательную таблицу, в каждой ячейке которой запишем сумму элементов (ij) ячейки, среднее (ij) ячейки и количество элементов (ij) ячейки.

Вспомогательная таблица:

	В1	В2	В3	Sстроки	строки	nстроки
S n	S n	S n
А1	1,1; 0,55; 2	-----	0,7; 0,35; 2	1,8	0,45
А2	1,2; 0,6; 2	1,2; 0,4; 3	1,1; 0,55; 2	3,5	0,5
Sстолбца	2,3	1,2	1,8	5,3
столбца	0,575	0,4	0,45		0,482
n столбца

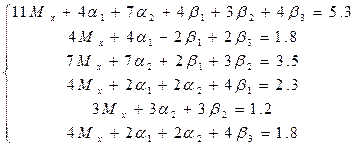
Преобразуем:

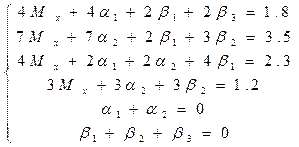
Дата добавления: 2014-01-14