Первый закон термодинамики – это закон сохранения энергии, согласно которому энергия ниоткуда не берется и никуда не девается, а только переходит из одной формы в другую

Мы живем в мире, где большинство событий необратимо. Необратимо и большинство химических изменений в мире, так что мир изменяется самопроизвольнов некотором направлении. Что значит «самопроизвольно»?

Самопроизвольным называется процесс, происходящий без затраты работы. Наоборот, в его результате работа может быть получена. Р абота — это мера упорядоченной передачи энергии от одной системы к другой. Иная возможность передачи энергии — теплота — мера передачи энергии от одного тела к другому путем неупорядоченных, хаотических столкновений частиц веществ, образующих эти тела, — явление теплопроводности.

Всякая система стремится перейти в состояние с наименьшей энергией. Самопроизвольно происходят только экзотермические процессы.

Однако существование обратимых химических реакций, которые, если они экзотермичны в одном направлении, то эндотермичны в другом, опровергает это утверждение. Закон сохранения энергии гласит, что энергия Мира постоянна. Если энергия какой-либо системы понижается, то неминуемо в другой системе она повышается. Для объяснения происходящих в мире изменений необходимо установить физическую причину.

Мерой беспорядка (W) служит физическая величина – энтропияS: чем выше значение энтропии, тем больше беспорядка, и чем оно ниже, тем больше порядка. Для реальных веществ величина W невообразимо велика, так что оперировать ею чрезвычайно неудобно. На практике мерой вероятности существования системы в том или другом состоянии является энтропия S, связанная с W уравнением Больцмана:

S = k ln W,

где k = R / N _A =1,38•10^–23 Дж/К – константа Больцмана, ln W – натуральный логарифм величины термодинамической вероятности

С увеличением W — числа способов, которым может быть реализовано данное состояние вещества, – возрастает энтропия S.

Размерность энтропии определяется размерностью константы Больцмана. Для вещества величина энтропии обычно дается в расчете на 1 моль, тогда ее размерность Дж/(К•моль). Наименьшая энтропия у веществ в кристаллическом состоянии и максимальная у газов. Жидкость в этом отношении занимает промежуточное положение. Строение идеального кристалла при абсолютном нуле градусов Кельвина совершенно однозначно, т.е. W = 1 и в соответствии с уравнением Больцмана S = 0. В идеально упорядоченном состоянии при температуре абсолютного нуля энтропия вещества равна 0. Таким образом, зная структуру вещества, можно вычислить его энтропию.

Чем больше в системе вещества, тем больше ее энтропия. Чем выше температура, тем больше число энергетических состояний, в которых могут находиться частицы, образующие данное вещество, тем больше энтропия. Это изменение энтропии определяется формулой S = Q/T, где S — изменение энтропии системы, Q — количество теплоты, поглощенной системой (тогда энтропия системы увеличивается, S > 0) или потерянной ею (тогда энтропия системы уменьшается, S < 0), T — абсолютная температура.

Все изложенные выше наблюдения могут помочь второй закон термодинамики: в изолированной системе самопроизвольно протекающие процессы увеличивают энтропию системы. (На основании второго закона термодинамики возникла теория тепловой смерти Вселенной.)

Следствие из второго закона термодинамики – высокая степень упорядоченности в системе возможна при поступлении энергии и вещества из-за пределов системы.

Третий закон термодинамики устанавливает, что энтропия физической системы при стремлении температуры к абсолютному нулю не зависит от параметров системы и остается неизменной. (В формулировке М.Планка энтропия S = 0 при T = 0 К.)

Энтропия жидкости обычно гораздо выше, чем энтропия твердого тела, а энтропия газа выше, чем энтропия соответствующей жидкости. Это означает, что с точки зрения второго закона термодинамики жидкостью быть более выгодно, чем твердым телом, а газом – выгоднее, чем жидкостью.

Таким образом, для самопроизвольного протекания реакции требуется, с одной стороны, уменьшение суммы энтальпий: если сумма энтальпий образования продуктов меньше суммы энтальпий образования реагентов, т.е. Н < 0, то такой процесс энергетически выгоден. С другой стороны, самопроизвольно может протекать лишь процесс, в котором сумма энтропий продуктов превышает сумму энтропий реагентов, т. е. изменение энтропии в ходе процесса должно быть положительным ( S > 0).

Возможно несколько вариантов изменения сумм энтальпий образования и энтропий веществ в ходе процесса.

1. Н < 0, S > 0. Процесс однозначно энергетически выгоден и может протекать самопроизвольно.

2. Н > 0, S < 0. Процесс однозначно энергетически невыгоден и не может протекать самопроизвольно.

3. Н < 0, S < 0. Уменьшение Н благоприятно для самопроизвольного протекания реакции, тогда как уменьшение S препятствует этому. (Неясно, возможно ли самопроизвольное протекание такой реакции.)

4. Н > 0, S > 0. Увеличение Н не способствует самопроизвольному протеканию реакции, однако возрастание S повышает ее вероятность. (Неясна возможность самопроизвольного протекания такой реакции.)

Самопроизвольный процесс в некоторой системе (где изменения и энтропии, и энтальпии относятся только к рассматриваемой системе) возможен, если:

S – H / Т > 0, или H – T S < 0. Значение этой функции (ее знак):

G = H – T S и определяет направление процесса. Роль арбитра, определяющего возможность самопроизвольного протекания реакции при постоянном давлении, играет энергия Гиббса, где T – абсолютная температура, К.

Функция состояния системы G называется энергией Гиббса, или изобарно-изотермическим потенциалом, или свободной энергией системы. В системе в качестве самопроизвольного возможен только тот процесс, в результате которого энергия Гиббса системы уменьшается, G < 0.

При G < 0 реакция может протекать самопроизвольно, а при G > 0 реакция термодинамически запрещена. Если G = 0, то реакционная система находится в состоянии равновесия (скорости прямой и обратной реакций равны).

Самопроизвольное протекание эндотермической реакции возможно лишь тогда, когда она сопровождается значительным увеличением энтропии.

Возможность или невозможность протекания реакции устанавливают с помощью уравнения Гиббса следующими способами.

1. Для температуры 25 °С на основе табличных данных рассчитывают G ⁰ по соотношению:

G ⁰ = Н ⁰– 298 S ⁰.

2. Для температуры, отличающейся от 25 °С, расчет проводят по соотношению:

G = G ⁰ + RT ln K _р.

K _р при данной температуре можно найти, преобразовав выражение для равновесия

G = 0 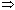G ⁰ + RT ln K _р = 0

к виду:

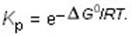
Это соотношение позволяет получить значение константы равновесия при любой температуре.

3. Для окислительно-восстановительных реакций выражение для энергии Гиббса при стандартных условиях принимает следующий вид:

G ⁰ = – nF 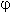⁰, где n – количество передаваемых электронов, F – постоянная Фарадея ( 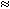96 500Кл/моль), 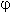⁰ – ЭДС реакции. Из этого выражения следует, что реакция протекает при положительном значении ЭДС.

4. Из условия равновесия реакции ( G = 0) имеем:

0 = Н – T S. Отсюда Т = Н / S – температура, при которой реакция находится в состоянии равновесия.

Термодинамика позволяет в принципе оценить возможность протекания химических реакций. Однако она ничего не говорит о реальных скоростях их протекания. Так, термодинамические расчеты показывают, что реакция окисления целлюлозы кислородом воздуха должна самопроизвольно протекать при комнатной температуре, чего на практике не наблюдается. Причина состоит в том, что у молекул не хватает энергии для осуществления процесса за обозримое время. Проблему времени достижения состояния равновесия решает наука о скоростях химических реакций – химическая кинетика.

Дата добавления: 2014-01-15