
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Эмпирические методы корреляционного анализа
|
|
|
|
Тесноту связи, наряду с корреляционным отношением, можно оценить и посредством использования других, более простых показателей.
1. Коэффициент Фехнера:
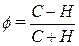 ,
, 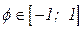 (8.1)
(8.1)
где С – совпадение знаков отклонений индивидуальных значений факторного признака от среднего значения и результативного признака от среднего значения: 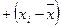 и
и 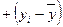 или
или 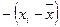 и
и 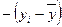 ;
;
Н – несовпадение знаков отклонений: 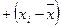 и
и 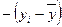 или
или 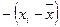 и
и 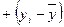 .
.
Знак при коэффициенте Фехнера характеризует направление связи:
«+» – связь прямая; «-» – связь обратная.
Численное значение показывает тесноту связи:
если  1 связь тесная; если
1 связь тесная; если  -1 связь слабая.
-1 связь слабая.
2. Коэффициент корреляции рангов Спирмена:
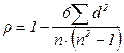 ,
, 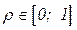 (8.2)
(8.2)
где d = Рx - Рy – разница рангов по двум признакам;
Рx, Рy – ранг по признаку x и y соответственно;
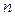 – количество рангов.
– количество рангов.
Для расчета этого показателя случайные величины х и у нумеруются по отдельности в порядке возрастания (или убывания), т.е. им присваивается определенный ранг (Рx и Рy) – порядковый номер в ряду.

| Важно! Если встречается несколько одинаковых значений х (или у), то каждому значению присваивается ранг, равный частному от деления суммы рангов, приходящихся на эти значения, на число этих равных значений. |
Затем ранги отдельных значений факторного признака Рx сопоставляют с рангами значений результативного признака Рy.
Следует отметить, что коэффициент корреляции рангов Спирмена (r) менее точен по сравнению с эмпирическим корреляционным отношением (h): если он получает крайние значения 0 и 1, то нельзя высказывать утверждение о функциональной связи между признаками или ее абсолютном отсутствии. Во всех других случаях, т.е. когда r не принимает крайних значений, он бывает довольно близким к h и позволяет довольно точно судить о тесноте связи между х и у.
Пример. Воспользуемся данными таблицы 8.1 для расчета коэффициентов Фехнера и Спирмена (табл. 8.3):
| Табельный номер рабочего | Факторный признак - стаж работы, лет xi | Результативный признак – среднемесячный уровень оплаты труда, тыс. руб. yi | Порядковый номер рабочего в ряду по возрастанию факторного признака | Порядковый номер рабочего в ряду по возрастанию результативного признака | Расчетные данные | ||||||
| Для расчета коэффициента Фехнера | Для расчета коэффициента Спирмена | ||||||||||
| 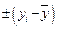
| С / Н | Рх | Ру | d=Рх- Ру | d2 | |||||
| 3,5 | – | – | С | ||||||||
| 3,7 | – | – | С | -2 | |||||||
| 3,8 | – | – | С | 7,5 | -4,5 | 20,25 | |||||
| 3,5 | – | – | С | ||||||||
| 3,7 | – | – | С | -2 | |||||||
| 3,5 | – | – | С | ||||||||
| 3,8 | – | – | С | 7,5 | -0,5 | 0,25 | |||||
| 3,9 | – | – | С | -2 | |||||||
| 4,1 | – | – | С | 10,5 | -0,5 | 0,25 | |||||
| 4,5 | – | Н | 10,5 | -3,5 | 12,25 | ||||||
| 4,1 | – | – | С | 10,5 | -0,5 | 0,25 | |||||
| 4,1 | – | – | С | 10,5 | -0,5 | 0,25 | |||||
| 4,6 | + | + | С | 16,5 | -0,5 | 0,25 | |||||
| 4,6 | + | + | С | 16,5 | -0,5 | 0,25 | |||||
| 4,7 | + | + | С | 16,5 | -4,5 | 20,25 | |||||
| 4,7 | + | + | С | 16,5 | -4,5 | 20,25 | |||||
| 4,7 | + | + | С | 16,5 | -4,5 | 20,25 | |||||
| 4,6 | + | + | С | 16,5 | -0,5 | 0,25 | |||||
| 3,7 | + | – | Н | 16,5 | 11,5 | 132,25 | |||||
| 4,7 | + | + | С | 16,5 | -4,5 | 20,25 | |||||
| 4,9 | + | + | С | 24,5 | -1,5 | 2,25 | |||||
| 4,7 | + | + | С | ||||||||
| 4,9 | + | + | С | 24,5 | -1,5 | 2,25 | |||||
| 4,5 | + | Н | |||||||||
| 4,5 | + | Н | |||||||||
| 5,0 | + | + | С | ||||||||
| 5,2 | + | + | С | ||||||||
| 6,0 | + | + | С | ||||||||
| 6,3 | + | + | С | -1 | |||||||
| 6,5 | + | + | С | -1 | |||||||
| Сумма | × | × | × | × | × | × | × | × | |||
| Среднее | 2,67 | 4,5 | × | × | × | × | × | × | × | × | × |
Коэффициент Фехнера 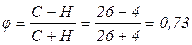 – связь прямая тесная.
– связь прямая тесная.
Расчет коэффициента Спирмена следует предварить расстановкой рангов факторного и результативного признаков (графы 4 и 5 таблицы 8.3).
Как видим, у рабочих № 1, 2, 3, 18 и 28 стаж работы xi одинаков и составляет 0 лет. Значит, и ранг по факторному признаку (Рх) у них должен быть одинаковым. Определим его как простое среднее из порядковых номеров этих пяти рабочих в ранжированном по факторному признакуряду (графа Г таблицы 8.3): 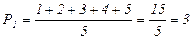 . Аналогично одинаковый ранг у следующих трех рабочих:
. Аналогично одинаковый ранг у следующих трех рабочих: 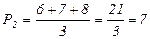 и т.д.
и т.д.
Аналогично расставляются ранги и для результативного признака. В этом случае расстановка рангов Ру осуществляется на основе порядковых номеров рабочих, находящихся в ранжированном массиве по возрастанию результативного признака – оплаты труда (графа Д таблицы 8.3). Тогда ранги будут такими, как приведены в графе 5 таблицы 8.3.
Коэффициент Спирмена 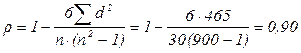 – связь тесная.
– связь тесная.
|
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 434; Нарушение авторских прав?; Мы поможем в написании вашей работы!