Этап. Измерение тесноты связи

Измерение тесноты связи так же, как и в корреляционном анализе, основано на расчете дисперсий для аналитической группировки. Однако составляющие общей дисперсии вычисляются несколько иначе:

- общая дисперсия, измеряющая общую вариацию результативного признака за счет действия всех факторов:

. (8.7)

- факторная (теоретическая) дисперсия, измеряющая вариацию результативного признака у за счет действия факторного признака х:

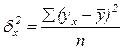. (8.8)

- остаточная дисперсия, характеризующая вариацию признака у за счет всех факторов, кроме х (т.е. при исключенном х):

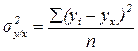. (8.9)

Согласно правилу сложения дисперсий:

. (8.10)

Оценивается теснота линейной связи с помощью ряда показателей:

1. Коэффициент детерминации – представляет собой удельный вес факторной дисперсии в общей и характеризует не всю вариацию у от факторного признака х, а лишь ту ее часть, которая соответствует линейному уравнению регрессии, т.е. показывает удельный вес вариации результативного признака, линейно связанной с вариацией факторного признака:

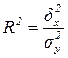. (8.11)

2. Индекс корреляции (теоретическое корреляционное отношение) – характеризует тесноту корреляционной зависимости, т.е. степень ее приближения к функциональной связи:

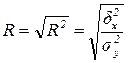
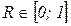. (8.12)

Если R = 1 – связь функциональная (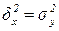, 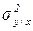=0 – эмпирически значения у_i совпадают с у_х, линия регрессии проходит через все эмпирические точки);

R = 0 – связь отсутствует ( =0 – все теоретические значения у_х совпадают со средними значениями у и линия регрессии проходит параллельно оси абсцисс);

R < 0,3 –связь слабая;

R > 0,7 – связь тесная.

Индекс корреляции пригоден для измерения тесноты связи при любой ее форме. Выравнивая у_i по разным функциям, можно по величине дисперсии, характеризующей остаточную вариацию (s²_у/х) судить о том, какая функция в наилучшей степени выравнивает эмпирическую линию связи (предпочтение отдается форме связи с меньшим значением остаточной дисперсии s²_у/х).

3. Линейный коэффициент корреляции – частный случай общего индекса корреляции. Его применение ограничено только линейной формой связи, однако он характеризует не только тесноту, но и направление связи:

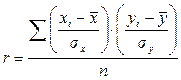. (8.13)

После преобразований он может быть представлен в более удобном виде:

. (8.14)

r =- 1…0 – связь обратная; r = 0…+1 – связь прямая;

r ®±1 – связь близка к функциональной.

Важно! При правильном подсчете численные значения индекса корреляции и линейного коэффициента корреляции практически совпадают.

Тогда коэффициент регрессии для уравнения прямой можно определить по формуле:

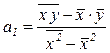. (8.15)

Дата добавления: 2014-01-15