
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные методы нахождения ранга матрицы
|
|
|
|
1).Метод единиц и нулей.
С помощью элементарных преобразований привести к виду, когда элементами матрицы являются 0 и 1. Тогда число оставшихся единиц (1) и определяет ранг матрицы.
ПРИМЕР. 
2).Метод окаймляющих миноров.
Определение. Минор 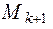 порядка (k+1),содержащий в себе минор
порядка (k+1),содержащий в себе минор 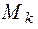 порядка k, называется окаймляющим минор
порядка k, называется окаймляющим минор 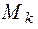 .
.
Если у матрицы А существует минор 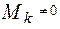 ,а все окаймляющие миноры
,а все окаймляющие миноры 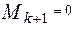 , то ранг А равен k.
, то ранг А равен k.
ПРИМЕР. 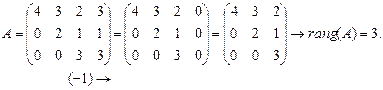
2.3.Обратная матрица.
Определение. Матрица 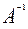 называется обратной к матрице А,если выполняется условие:
называется обратной к матрице А,если выполняется условие: 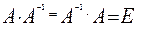 ,где Е- единичная матрица того же порядка, что и А.
,где Е- единичная матрица того же порядка, что и А.
Матрицей союзной к матрице А, называется матрица
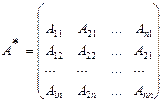 ,
,
где 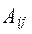 -алгебраические дополнения элемента
-алгебраические дополнения элемента 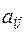 данной матрицы А (определяются также как и алгебраические дополнения элемента определителя).
данной матрицы А (определяются также как и алгебраические дополнения элемента определителя).
Итак, 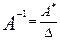 ,т.е.
,т.е. 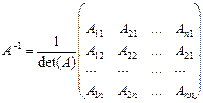 .
.
§3.Системы линейных уравнений (СЛАУ).
3.1.Основные понятия.
Определение. Системой линейных алгебраических уравнений, содержащей m уравнений и n неизвестных,называется система вида
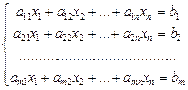 , (3.1)
, (3.1)
где числа 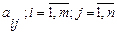 называются коэффициентами системы, числа
называются коэффициентами системы, числа
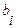 -свободными членами. Подлежат нахождению числа
-свободными членами. Подлежат нахождению числа 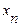 .
.
Такую систему удобно записывать в компактной матричной форме
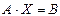 .
.
Здесь А –матрица коэффициентов системы,называемая основной матрицей:
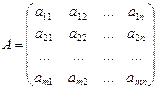 ,
,
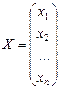 - вектор-столбец из неизвестных
- вектор-столбец из неизвестных 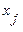 ,
,
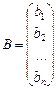 - вектор-столбец из свободных членов
- вектор-столбец из свободных членов 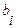 .
.
Определение. Расширенной матрицей системы называется матрица А1 системы,дополненная столбцом свободных членов
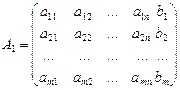 .
.
Определение. Решением системы называется n значений неизвестных 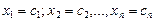 при подстановке которых все уравнения системы обращаются в верные равенства.Всякое решение системы можно записать в виде матрицы-столбца
при подстановке которых все уравнения системы обращаются в верные равенства.Всякое решение системы можно записать в виде матрицы-столбца
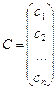 .
.
Совместной системой называется система,если она имеет хотя бы одно решение,
несовместной- если она не имеет ни одного решения.
Определенной называется совместная система,если она имеет единственное решение, неопределенной - если она имеет более одного решения.В последнем случае каждое ее решение называется частным решением системы.Совокупность всех частных решений называется общим решением.
Решить систему- это значит выяснить,совместна она или не совместна.Если система совместна, найтиее общее решение.
3.2.Решение СЛАУ. Теорема Кронекера-Капелли.
ТЕОРЕМА Кронекера-Капелли. Система линейных алгебраических уравнений (3.1) совместна тогда и только тогда,когда ранг основной матрицы этой системы равен рангу ее расширенной матрицы.
Т.е. система (3.1) совместна тогда и только тогда,когда r(А)=r(А1)=r.
В этом случае число r называется рангом системы (1).
ТЕОРЕМА. Если ранг совместной системы равен числу неизвестных,то система
имеет единственное решение.
ТЕОРЕМА. Если ранг совместной системы меньше числа неизвестных,то система
имеет бесчисленное множество решений.
Правило решения произвольной системы линейных уравнений.
1).Найти ранги основной и расширенной матриц системы.Если r(А)≠r(А1), то система несовместна.
2).Если r(А)=r(А1)=r. Система совместна.
Найти какой-либо базисный минор порядка r (минор,порячдок которого определяет ранг матрицы,называется базисным).Взять r уравнений,из коэффициентов которых составлен базисный минор(остальные уравнения отбросить). Неизвестные,коэффициенты которых входят в базисный минор,называют главными и оставляют слева,а остальные (n-r) неизвестных называют свободными и переносят в правые части уравнений.
3).Найти выражения главных неизвестных через свободные.Получено общее решение системы.
4).Придавая свободным неизвестным произвольные значения,получим соответствующие значения главных неизвестных.Таким образом можно найти частные решения исходной системы уравнений.
ПРИМЕР. Исследовать на совместность систему 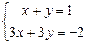 .
.
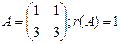 ,
, 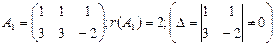 .
.
Таким образом, r(А)≠r(А1), следовательно система несовместна.
ПРИМЕР. Исследовать на совместность систему 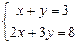 .
.
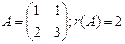 ;
; 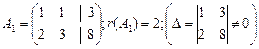 .
.
Таким образом, r(А)=r(А1) - система совместна.
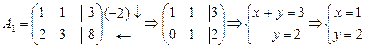 - решение системы.
- решение системы.
ПРИМЕР. Решить систему 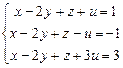 .
.
r(А)=r(А1)=2. Берем два первых уравнения: 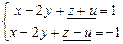 .
. 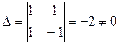 ,
,
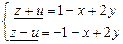 ,
, 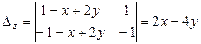 ,
, 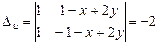 .
.
Следовательно, z= -х+2у, u=1- общее решение.
Пусть,например, х=0,у=0, получаем одно из частных решений: х=0,у=0,z=0,u=1.
3.3.Решение СЛАУ методом Крамера, матричным методом и
методом Гаусса.
Пусть дана система n линейных уравнений с n неизвестными
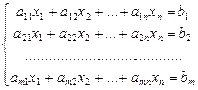
или в матричной форме А·Х=В.
Основная матрица А такой системы квадратная.Определитель этой матрицы
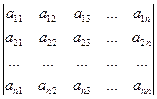
Называется определителем системы. Если определитель системы отличен от нуля,то система называется невырожденной.
Найдем решение данной системы уравнений в случае 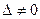 .
.
Умножив обе части уравнения А·Х=В слевана матрицу 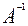 , получим
, получим
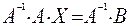 .Поскольку
.Поскольку 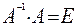 и
и 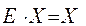 ,то
,то
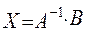 . (3.2)
. (3.2)
Отыскание решения системы по данной формуле (3.2)называют матричным способом решения системы.
Матричное равенство (3.2) запишем в виде:
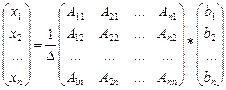 ,
,
то есть 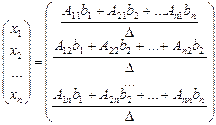 .
.
Отсюда следует,что 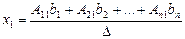 ,
,
………………………….
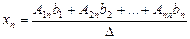 .
.
Но 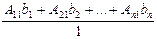 есть разложение определителя
есть разложение определителя
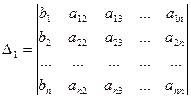
По элементам первого столбца.Определитель 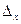 получается из определителя ∆ путем замены первого столбца коэффициентов столбцом из свободных членов.Итак,
получается из определителя ∆ путем замены первого столбца коэффициентов столбцом из свободных членов.Итак, 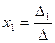 ,аналогично
,аналогично 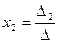 ,где
,где 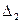 получен из ∆ путем замены второго столбца коэффициентов столбцом из свободных членов;
получен из ∆ путем замены второго столбца коэффициентов столбцом из свободных членов; 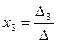 ,…
,…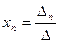 .
.
Формулы 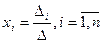 (3.3)
(3.3)
называются Формулами Крамера.
Итак, невырожденная система n линейных уравнений с n неизвестными имеет единственное решение,которое может быть найдено матричным способом (3.2) или по формулам Крамера (3.3).
ПРИМЕР. Решить систему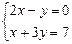 .
.
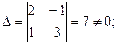
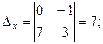
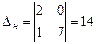 . Значит
. Значит 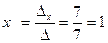 ,
,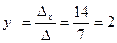 .
.
Одним из наиболее универсальных и эффективных методов решений линейных алгебраических систем является Метод Гаусса, состоящий в последовательном исключении неизвестных.
Пусть дана система 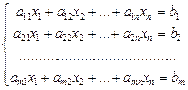 . (3.4)
. (3.4)
Процесс решения по методу Гаусса состоит из двух этапов.На первом этапе (прямой ход) система приводится к ступенчатому( в частности,к треугольному) виду.Приведенная система имеет вид:
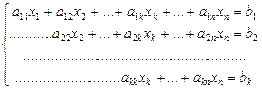 ,
,
где k≤n, 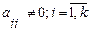 . Коэффициенты
. Коэффициенты 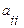 называются главными элементами системы.
называются главными элементами системы.
На втором этапе(обратный ход) идет последовательное определение неизвестных из этой ступенчатой системы.
Замечания: 1). Если ступенчатая система оказывается треугольной,т.е. k=n, то исходная система имеет единственное решение.Из последнего уравнения находим 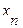 ,из предпоследнего уравнения
,из предпоследнего уравнения 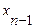 ,далее поднимаясь по системе вверх,найдем все остальные неизвестные (
,далее поднимаясь по системе вверх,найдем все остальные неизвестные (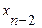 ,…,
,…,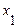 ).
).
2). На практике удобнее работать не с системой (3.4),а с расширенной ее матрицей,выполняя все элементарные преобразования над ее строками.Удобно,чтобы коэффициент 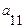 был равен 1(уравнения переставить местами или разделить обе части уравнения на
был равен 1(уравнения переставить местами или разделить обе части уравнения на 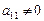 ).
).
ПРИМЕР. Решить систему методом Гаусса: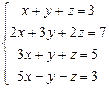 .
.
Произведем элементарные преобразования над строчками расширенной матрицы системы:
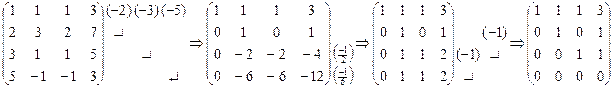 .
.
Полученная матрица соответствует системе 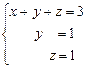 , найдем
, найдем 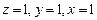 .
.
ПРИМЕР. Решить систему методом Гаусса: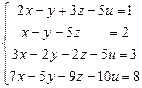 .
.
Решение:
В результате элементарных преобразований над расширенной матрицы системы: 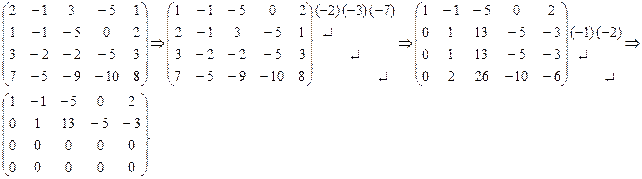 .
.
Исходная система свелась к ступенчатой: 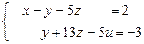 , общее решение системы
, общее решение системы 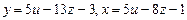 .Если положить,например,
.Если положить,например, 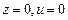 ,то найдем одно из частных решений этой системы
,то найдем одно из частных решений этой системы 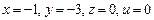 .
.
3.4.Системы линейных однородных уравнений.
Пусть дана система линейных однородных уравнений
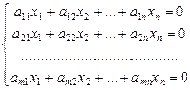 .
.
Очевидно,что однородная система всегда совместна (r(А)=r(А1)), она имеет нулевое(тривиальное) решение х1=х2=…=хn=0.
ТЕОРЕМА 1. Для того,чтобы система однородных уравнений имела ненулевые решения,необходимо и достаточно,чтобы ранг r ее основной матрицы был меньше числа n неизвестных,т.е. r<n.
ТЕОРЕМА 2. Для того,чтобы однородная система n линейныхуравнений
с n неизвестными имела ненулевые решения,необходимо и достаточно,чтобы ее определитель ∆ был равен нулю,т.е. ∆=0.
Если ситема имеет ненулевые решения,то ∆=0. Ибо при ∆≠0 система имеет только единственное,нулевое решение.Если же ∆=0, то ранг r основной матрицы системы меньше числа неизвестных,т.е. r<n. Значит система имеет бесконечное множество (ненулевых) решений.
ПРИМЕР. Решить систему: 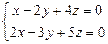 .
.
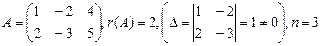 .
.
Поскольку r<n, то система имеет бесчисленное множество решений.Найдем их
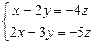 .
.
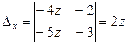 ,
,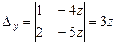 ,следовательно
,следовательно 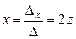 ,
,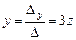 -общее решение.
-общее решение.
Положив 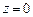 получаем одно частное решение:
получаем одно частное решение: 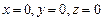 ,положив
,положив 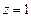 ,получаем второе частное решение
,получаем второе частное решение 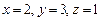 и т.д.
и т.д.
Глава 2.ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ И
n-МЕРНОЕ ВЕКТОРНОЕ ПРОСТРАНСТВО.
§1.Векторы и действия над ними.
Величины,которые полностью определяются своим численным значением, называются скалярными. Примерами скалярных величин являются: площадь,длина,объем,температура,работа,масса.
Другие величины,например сила,скорость,ускорение,определяются не только своим числовым значением,но и направлением.такие величины называются векторными. Векторная величина геометрически изображается с помощью вектора.
Определение. Вектор – это направленный прямолинейный отрезок,т.е. отрезок,имеющий определенную длину и определенное направление.
Если А – начало вектора, В – его конец, то вектор обозначается символом  или
или  . Вектор
. Вектор 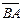 (у него начало в точке В, а конец в точке А) называется противоположным вектору
(у него начало в точке В, а конец в точке А) называется противоположным вектору  .Вектор,противоположный вектору
.Вектор,противоположный вектору  обозначается
обозначается 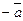 .
.
Определение. Длиной или модулем вектора  называется длина отрезка и
называется длина отрезка и
обозначается 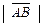 .
.
Определение. Вектор,длина которого равна нулю,называется нулевым вектором и
обозначается 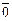 .Нулевой вектор направления не имеет.
.Нулевой вектор направления не имеет.
Определение. Вектор,длина которого равна единице,называется единичным
вектором и обозначается 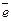 . Единичный вектор,направление которого
. Единичный вектор,направление которого
совпадает с направлением вектора  ,называется ортом вектора
,называется ортом вектора  и
и
обозначается 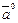 .
.
Определение. Векторы  и
и  называются коллинеарными, если они лежат на одной
называются коллинеарными, если они лежат на одной
прямой или на параллельных прямых,записывают  ║
║  . Коллинеарные векторы могут быть направлены одинаково или противоположно.
. Коллинеарные векторы могут быть направлены одинаково или противоположно.
Определение. Два вектора называются равными (  =
=  ),если они коллинеарны,
),если они коллинеарны,
одинаково направлены и имеют одинаковые длины.
Из определения равенства векторов следует,что вектор можно переносить параллельно самому себе,а начало вектора помещать в любую точку О пространства.
Равные векторы также называют свободными.
Определение. Три вектора в пространстве называются компланарными, если они
лежат в одной плоскости или в параллельных плоскостях.
Если среди трех векторов хотя бы один нулевой или два любые коллинеарны,то такие векторы компланарны.
Под линейными операциями над векторами понимают операции сложения и вычитания векторов,а также умножение вектора на число.
Пусть  и
и  - два произвольных вектора,возьмем произвольную точку О и построим вектор
- два произвольных вектора,возьмем произвольную точку О и построим вектор 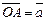 . От точки А отложим вектор
. От точки А отложим вектор 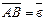 . Вектор
. Вектор 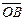 , соединяющий начало первого вектора с концом второго,называется суммой векторов
, соединяющий начало первого вектора с концом второго,называется суммой векторов  и
и  :
: 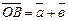 (Рис. 1).
(Рис. 1).



 +
+ 
Рис. 1.
Данное правило сложения векторов называют правилом треугольника.
Сумму двух векторов можно построить также по правилу параллелограмма
(Рис. 2).





 +
+ 
Рис. 2.
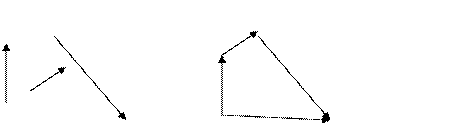
Сложение трех векторов  ,
,  ,
, 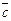 показано на рисунке 3.
показано на рисунке 3.


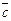
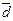 =
= +
+  +
+ 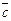
Рис.3.
Под разностью векторов  и
и  понимается вектор
понимается вектор 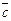 =
= -
- такой,что
такой,что  =
=  +
+ 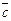 (Рис. 4).
(Рис. 4).
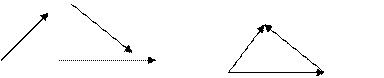



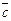 =
= -
- 

Рис. 4.
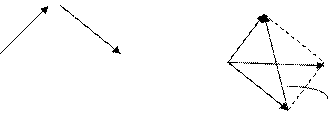
Необходимо отметить,что в параллелограмме,построенном на векторах
 и
и  ,одна направленная диагональ является суммой векторов
,одна направленная диагональ является суммой векторов  и
и  ,а другая-разностью(Рис. 5).
,а другая-разностью(Рис. 5).

 +
+ 


 -
- 
Рис. 5.
Произведением вектора  на скаляр(число) λ называется вектор λ
на скаляр(число) λ называется вектор λ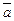 (или
(или  λ),
λ),
который имеет длину | λ |*| 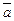 |,коллинеарен вектору
|,коллинеарен вектору 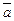 , имеет направление вектора
, имеет направление вектора 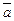 ,если λ>0 и противоположное направление,если λ<0. Например,если дан вектор
,если λ>0 и противоположное направление,если λ<0. Например,если дан вектор 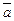 , то векторы 3
, то векторы 3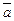 и -2
и -2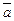 будут иметь вид:
будут иметь вид:

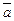 3
3 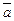 -2
-2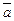 .
.
Из определения произведения вектора на число следуют свойства этого произведения:
1).если  =λ
=λ ,то
,то  ║
║  .
.
Наоборот,если  ║
║  (
( ≠
≠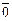 ),то при некотором λ верно равенство
),то при некотором λ верно равенство  =λ
=λ ;
;
2).всегда  =
=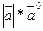 ,т.е. каждый вектор равен произведению его модуля на орт.
,т.е. каждый вектор равен произведению его модуля на орт.
Линейные операции над векторами обладают следующими свойствами:
1.  +
+ =
= +
+ , 4. (λ 1+λ2) *
, 4. (λ 1+λ2) * =λ1*
=λ1* +λ2 *
+λ2 * ,
,
2. ( +
+ )+
)+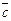 =
= +(
+( +
+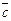 ), 5. λ *(
), 5. λ *( +
+ )=λ*
)=λ* +λ *
+λ * .
.
3. λ 1*(λ2 * )=λ1*λ2*
)=λ1*λ2* ,
,
Эти свойства позволяют проводить преобразования в линейных операциях с вектором так,как это делается в обычной алгебре: слагаемые менять местами,вводить скобки,группировать,выносить за скобки как скалярные,так и векторные общие множители.
Рассмотрим в пространстве прямоугольную систему координат Охуz. Выделим на координатных осях Ох,Оу,Оz единичные векторы(орты),обозначаемые 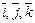 соответственно.
соответственно.
z
у
х
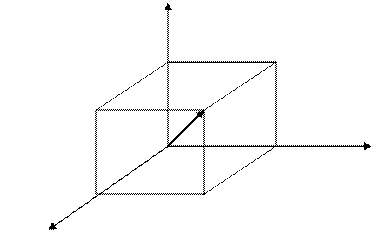
Выберем произвольный вектор  пространства и совместим его начало с началом координат.Найдем проекции вектора
пространства и совместим его начало с началом координат.Найдем проекции вектора  на координатные оси. Проведем через конец вектора
на координатные оси. Проведем через конец вектора  плоскости,параллельные координатным плоскостям.Получим прямоугольный параллелепипед.,одной из диагоналей которого является вектор
плоскости,параллельные координатным плоскостям.Получим прямоугольный параллелепипед.,одной из диагоналей которого является вектор  . Обозначим проекции вектора
. Обозначим проекции вектора  на оси Ох,Оу,Оz соответственно через
на оси Ох,Оу,Оz соответственно через 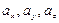 .Тогда
.Тогда
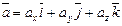 .
.
Эта формула является основной в векторном исчислении и называется разложением вектора по ортам координатных осей.
Числа 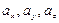 называются координатами вектора
называются координатами вектора  , т.е. координаты вектора есть его проекции на соответствующие координатные оси.Векторное равенство часто записывают в символическом виде:
, т.е. координаты вектора есть его проекции на соответствующие координатные оси.Векторное равенство часто записывают в символическом виде: 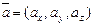 .
.
Зная проекции вектора  ,можно легко найти выражение для модуля вектора:
,можно легко найти выражение для модуля вектора:
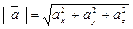 ,
,
т.е. модуль вектора равен квадратному корню из суммы квадратов его проекций на оси координат.
Пусть углы вектора  с осями Ох,Оу,Оz соответственно равны α,β,γ.
с осями Ох,Оу,Оz соответственно равны α,β,γ.
По свойству проекции вектора на ось,имеем:
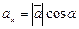 ,
, 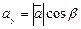 ,
, 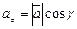 или что то же самое
или что то же самое 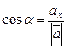 ,
,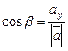 ,
,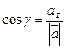 .
.
Числа 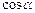 ,
,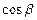 ,
,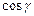 называются направляющими косинусами вектора
называются направляющими косинусами вектора  .
.
При чем, сумма квадратов направляющих косинусов ненулевого вектора равна единице: 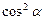 +
+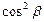 +
+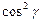 =1.
=1.
Координатами единичного вектора 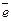 являются числа
являются числа 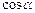 ,
,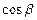 ,
,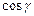 ,т.е.
,т.е.
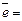 (
(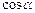 ,
,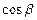 ,
,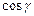 ).
).
Т.е. задав координаты вектора можно определить его модуль и направление,т.е. сам вектор.
Если даны два вектора 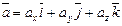 и
и  ,то
,то
1). 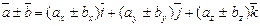 или кратко
или кратко 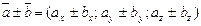 ,т.е при сложении(вычитании) векторов их одноименные координаты складываются (вычитаются).
,т.е при сложении(вычитании) векторов их одноименные координаты складываются (вычитаются).
2). 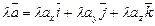 , кратко
, кратко 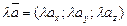 ,т.е при умножении векторов на скаляр координаты вектора умножаются на этот скаляр.
,т.е при умножении векторов на скаляр координаты вектора умножаются на этот скаляр.
Условие коллинеарности векторов заключается в том,что проекции коллинеарных векторов пропорциональны:
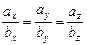 .
.
Верно и обратное:векторы,имеющие пропорциональные координаты,коллинеарны.
Координаты вектора 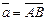 ,если известны координаты точек
,если известны координаты точек 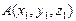 и
и 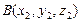 , равны разностям соответствующих координат его конца и начала:
, равны разностям соответствующих координат его конца и начала:
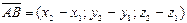 .
.
§2.Скалярное и векторное произведения векторов.Смешанное
произведение.
Скалярное произведение.
Определение. Скалярным произведением двух ненулевых векторов 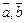 называется число, равное произведению длин этих векторов на косинус угла между ними:
называется число, равное произведению длин этих векторов на косинус угла между ними:
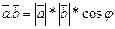 ,
,
где 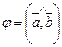 .
.
Свойства скалярного произведения.
1).Скалярное произведение обладает переместительным свойством:
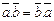 ,
,
при чем 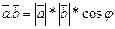 и
и 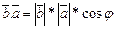 .
.
2). Скалярное произведение обладает сочетательным свойством относительно скалярного множителя: 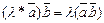 .
.
3). Скалярное произведение обладает распределительным свойством:
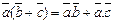 .
.
4).Скалярный квадрат вектора равен квадрату его длины: Скалярное произведение обладает переместительным свойством:
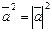 ,
,
в частности: 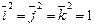 .
.
ПРИМЕР. Найти длину вектора 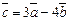 ,если
,если 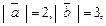
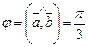 .
.
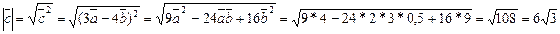 .
.
5).Если векторы 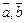 (ненулевые) взаимно перпендикулярны,то их скалярное произведение равно нулю,т.е. если
(ненулевые) взаимно перпендикулярны,то их скалярное произведение равно нулю,т.е. если 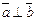 , то
, то 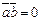 .Справедливо и обратное утверждение: если
.Справедливо и обратное утверждение: если 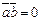 и
и 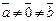 , то
, то 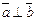 .
.
Если векторы заданы в форме: 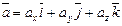 и
и  , то скалярное произведение равно:
, то скалярное произведение равно: 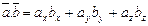 .
.
Итак, скалярное произведение векторов равно сумме произведений их одноименных
координат.
ПРИМЕР. Доказать,что диагонали четырехугольника,заданного координатами вершин
А(-4,-4,4), В(-3,2,2), С(2,5,1), D(3,-2,2),взаимно перпендикулярны.
Векторы  и
и 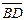 , лежащие на диагоналях четырехугольника,равны:
, лежащие на диагоналях четырехугольника,равны: 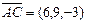 и
и 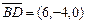 ,скалярное произведение этих векторов равно:
,скалярное произведение этих векторов равно: 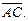
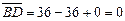 .
.
Отсюда следует,что 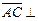
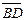 . Диагонали четырехугольника АВСD взаимно перпендикулярны.
. Диагонали четырехугольника АВСD взаимно перпендикулярны.
Угол между векторами.
Определение угла φ между ненулевыми векторами 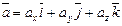 и
и  сводится к нахождению cosφ:
сводится к нахождению cosφ:
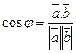 ,т.е.
,т.е. 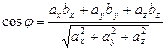 .
.
Отсюда следует условие перпендикулярности ненулевых векторов 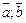 :
:
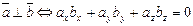 .
.
ПРИМЕР. Определить угол φ между векторами 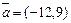 и
и 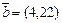 .
.
Скалярное произведение векторов равно:  ,
,
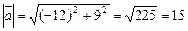 ,
, 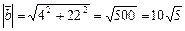 ,тогда
,тогда
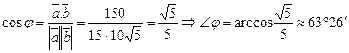 .
.
Векторное произведение.
Определение. Векторным произведением вектора  на вектор
на вектор 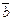 называется вектор
называется вектор 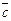 ,
,
который: 1)перпендикулярен векторам  и
и 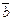 ,т.е.
,т.е. 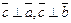 ;
;
2)имеет длину,численно равную площади параллелограмма,построенного на векторах  и
и 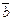 как на сторонах,т.е.
как на сторонах,т.е.
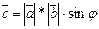 ,где
,где 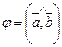 ;
;
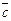
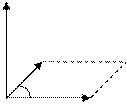
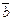
S

3)векторы 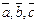 образуют правую тройку(если с конца третьего вектора
образуют правую тройку(если с конца третьего вектора 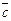 кратчайший поворот от первого вектора
кратчайший поворот от первого вектора  ко второму вектору
ко второму вектору 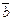 виден совершающимся против часовой стрелки).
виден совершающимся против часовой стрелки).
Векторное произведение обозначается 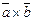 .
.
Свойства векторного произведения.
1).При перестановке сомножителей векторное произведение меняет знак,т.е. 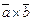 =
=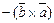 .
.
2).Векторное произведение обладает сочетательным свойством относительно скалярного множителя,т.е. 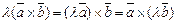 .
.
3).Два ненулевых вектора 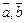 коллинеарны тогда и только тогда,когда их векторное произведение равно нулевому вектору,т.е.
коллинеарны тогда и только тогда,когда их векторное произведение равно нулевому вектору,т.е.  ║
║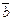
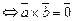 .
.
4).Векторное произведение обладает распределительным свойством:
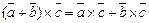 .
.
Выражение векторного произведения через координаты.
Удобно использовать таблицу векторного произведения векторов 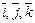 :
:
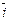
| 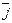
| 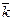
| |
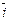
| 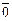
| 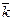
| - 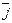
|
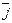
| - 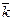
| 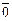
| 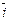
|
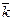
| 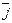
| -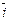
| 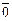
|
и схему,чтобы не ошибиться со знаком:
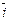

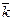 .
. 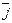
если направление кратчайшего пути от первого вектора ко второму совпадает
с направлением стрелки,то произведение равно третьему вектору,если не совпадает-третий вектор берется со знаком «минус».
Вычисление векторного произведения осуществляется по формуле:
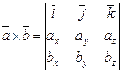 .
.
ПРИМЕР. Векторы 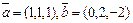 являются ортогональными,поскольку их скалярное произведение равно нулю:
являются ортогональными,поскольку их скалярное произведение равно нулю: 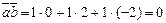 ,поэтому угол между этими векторами равен 90º.
,поэтому угол между этими векторами равен 90º.
Векторное произведение равно:
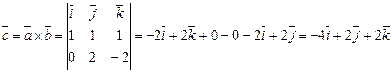 ,
,
Модуль векторного произведения равен:
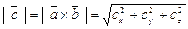 =
=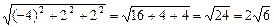 .
.
Нахождение площади параллелограмма и треугольника.
Согласно определению векторного произведения векторов 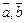
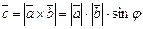 ,где
,где 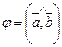 ; т.е. Sпараллелограмма =
; т.е. Sпараллелограмма = 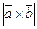 ,следовательно
,следовательно
Sтреугольника = 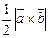 .
.
Смешанное произведение.
Рассмотрим произведение векторов 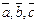 ,составленное следующим образом: (
,составленное следующим образом: (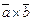 ).
).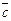 . Первые два вектора перемножаются векторно,а их результат скалярно на третий вектор.Такое произведение называется векторно-скалярным
. Первые два вектора перемножаются векторно,а их результат скалярно на третий вектор.Такое произведение называется векторно-скалярным
или смешанным произведением трех векторов. Смешанное произведение представляет собой некоторое число.
Модуль смешанного произведения трех векторов равен обьему параллелепипеда, построенного на этих векторах.
Свойства смешанного произведения.
1.Смешанное произведение не меняется при циклической перестановке его сомножителей,т.е. (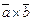 ).
).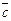 =(
=(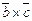 ).
). =(
=(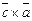 ).
).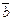 .
.
2. Смешанное произведение не меняется при перемене местами знаков векторного и скалярного умножения,т.е. (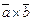 ).
).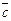 =
= .(
.(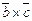 ).
).
3. Смешанное произведение меняет свой знак при перемене мест любых двух векторов-сомножителей,т.е. (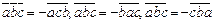 ).
).
4.Смешанное произведение ненулевых векторов 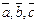 равно нулю тогда и только тогда,когда они компланарны.
равно нулю тогда и только тогда,когда они компланарны.
Выражение смешанного произведения через координаты.
Пусть заданы векторы: 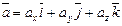 ,
,  и
и 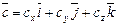 , смешанное произведение равно:
, смешанное произведение равно: 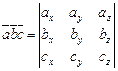 .
.
Установление компланарности векторов.
Векторы 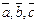 компланарны тогда и только тогда,когда их смешанное произведение равно нулю (
компланарны тогда и только тогда,когда их смешанное произведение равно нулю (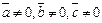 ):
):
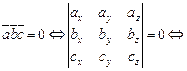 векторы компланарны.
векторы компланарны.
Определение обьемов параллелепипеда и треугольной пирамиды.
Обьем параллелепипеда,построенного на векторах 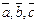 вычисляется по формуле:
вычисляется по формуле:
Vпараллелепипеда = 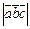 ,а обьем треугольной пирамиды,построенной на этих же векторах,равен Vтреуг.пирамиды =
,а обьем треугольной пирамиды,построенной на этих же векторах,равен Vтреуг.пирамиды = 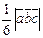 .
.
ПРИМЕР. Вершинами пирамиды служат точки А(1,2,3), В(0,-1,1),С(2,5,2) и D(3,0,-2). Найти обьем пирамиды.
Найдем векторы 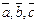 :
: 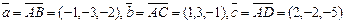 .
.
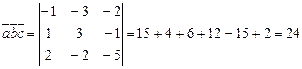 ,
,
следовательно Vтреуг.пирамиды = 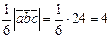 .
.
§3.Размерность и базис векторного пространства.
Рассмотрим такое множество R элементов х,у,z,…,в котором для любых двух элементов х€R и у€R определена сумма х+у €R и для любого элемента х €R и любого действительного числа λ определено произведение λ x €R.
Если сложение элементов множества R и умножение элемента этого множества на действительное число удовлетворяет следующим условиям:
1. х+у=у+х;
2. (х+у)+z=x+(y+z);
3. существует такой элемент 0 €R (нуль-элемент),что х+0=х для любого х €R;
4. для каждого элемента х €R существует элемент у €R такой что х+у=0
(в дальнейшембудем писать у=-х, т.е. х+(-х)=0);
5. 1· х = х;
6. λ(μ x)= (λμ) x;
7. (λ+μ) x= λ х+ μ x;
8. λ(x+у)= λ x+ λ у,
То множество R называется линейным (или векторным) пространством, а элементы х,у,z этого пространства- векторами.
Например,множество всех геометрических векторов является линейным пространством,так как для элементов этого множества определены действия сложения и умножения на число,удовлетворяющие сформулированным условиям.
Разностью двух векторов х,у линейного пространства называется такой вектор v этого пространства,что у+v=х. Разность векторов х,у обозначают через х-у,
т.е. х-у=v.
Справедливы следующие теоремы:
1.В каждом линейном пространстве существует только один нуль-элемент.
2.Для каждого элемента линейного пространства существует только один противоположный элемент.
3.Для каждого элемента х €R выполняется равенство 0· х =0.
4.Для любого действительного числа λ и 0 €R выполняется равенство λ· 0=0.
5.Из равенства λ· х=0 следует одно из двух равенств: λ=0 или х=0.
6.Элемент (-1)· х является противоположным для элемента х.
Пусть х,у,z,…,и- какие-либо векторы линейного пространства R. Вектор,определяемый равенством
v= α x+ β у+ γ z+…+ λ и,
где α,β,γ,...λ – действительные числа,также принадлежат линейному пространству R. Этот вектор называется линейной комбинацией векторов х,у,z,…,и.
Пусть линейная комбинация векторов х,у,z,…,и является нуль-вектором,т.е. 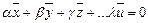 . (3.1)
. (3.1)
Определение. Векторы х,у,z,…,и называются линейно независимыми,если равенство (3.1) выполняется лишь при α=β=γ=...=λ =0. Если же равенство (3.1)может выполняется и в том случае,когда не все числа α,β,γ,...λ равны нулю,то говорят,что векторы х,у,z,…,и линейно независимы.
Если в линейном пространстве R имеется n линейно независимых векторов,то любые (n+1) векторов этого пространства линейно зависимы,то пространство R называют n- мерным – d(R)=n. Пространство,в котором можно найти сколь угодно много линейно независимых векторов,называется бесконечномерным, т.е.
d(R)=∞.
Совокупность n линейно независимых векторов n- мерного линейного пространства называется базисом.
ТЕОРЕМА. Каждый вектор линейного n-мерного пространства может быть единственным образом представлен в виде линейной комбинации векторов базиса.
Так,если f1, f2,…,fn –базис n -мерного линейного пространства R,то любой вектор х €R
может быть единственным образом представлен в виде
х= ξ1 f1 + ξ2f2 + …+ ξnfn.
Таким образом, вектор х в базисе f1, f2,…,fn определяется единственным образом с помощью чисел ξ1, ξ2,…+ ξn. Эти числа называются координатами вектора х в данном базисе.
Для определения размерности линейного пространства полезно использовать следующую теорему:
ТЕОРЕМА. Если любой вектор линейного пространства R может быть представлен в виде линейной комбинации линейно независимых векторов f 1, f2,…,fn, то d(R) = n ( а следовательно,векторы f1, f2,…,fn образуют базис в пространстве R).
ПРИМЕР. Дано линейное пространство всевозможных пар упорядоченных действительных чисел.Доказать,что векторы f1 =(1,2) и f 2=(3,4) образуют базис данного линейного пространства.Найти координаты вектора х =(7,10) в этом базисе.
Поскольку 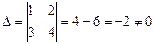 ,следовательно данные векторы образуют базис.
,следовательно данные векторы образуют базис.
Вектор х =(7,10) в этом базисе может быть представлен в виде: 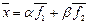 или в координатной форме:
или в координатной форме: 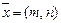 .Задача сводится к определению
.Задача сводится к определению 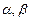 из системы уравнений:
из системы уравнений: 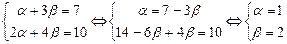 .
.
Отсюда 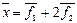 .
.
§4.Преобразование координат при переходе к новому базису.
Пусть в n- мерного линейного пространств имеется два базиса f 1, f2,…,fn (старый)и f´1, f´2,…,f´n (новый).Даны зависимости,выражающие каждый вектор нового базиса через векторы старого базиса:
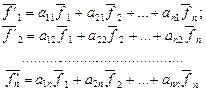 .
.
Определение. Матрицу 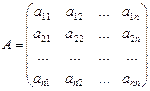 называют матрицей перехода от старого базиса к новому.
называют матрицей перехода от старого базиса к новому.
Пусть дан какой-либо вектор х,при чем 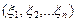 - координаты этого вектора в старом базисе,а
- координаты этого вектора в старом базисе,а 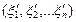 - его координаты в новом базисе.При этом старые координаты вектора х выражаются через новые координаты этого вектора по формулам:
- его координаты в новом базисе.При этом старые координаты вектора х выражаются через новые координаты этого вектора по формулам: 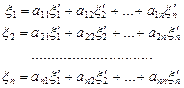 , которые называются формулами преобразования координат.
, которые называются формулами преобразования координат.
ПРИМЕР. Дан вектор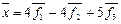 .Разложить этот вектор по новому базису,связанному со старым базисом уравнениями
.Разложить этот вектор по новому базису,связанному со старым базисом уравнениями 
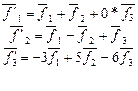 .
.
Исключив f1, f2,…,fn из системы уравнений 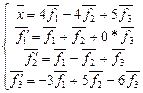 .
.
Получаем 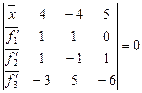 ,раскроем этот определитель по элементам первого столбца выразим х через f´1, f´2,…,f´n.
,раскроем этот определитель по элементам первого столбца выразим х через f´1, f´2,…,f´n.
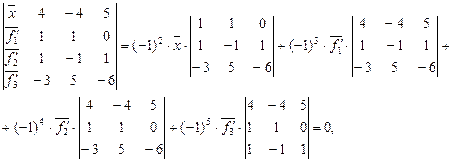
т.е. 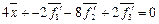 , отсюда
, отсюда 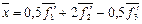 .
.
§5.Линейные преобразования.
5.1.Основные понятия и матрица линейного преобразования.
Будем говорить,что в линейном пространстве R задано преобразование А, если каждому вектору x €R по некоторому правилу поставлен в соответствие вектор А x €R. Преобразование А называется линейным, если для любых векторов х,у и для любого действительного числа λ выполняются равенства
А(x+у)= А x+ А у, А(λ x)= λА x.
Линейное преобразование называется тождественным, если оно преобразует любой вектор х в самого себя.Тождественное линейное преобразование обозначается через Е. Таким образом, Е х=х.
Пусть в n- мерном линейном пространстве R, базис которого f1, f2,…,fn задано линейное преобразование А.
|
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 1073; Нарушение авторских прав?; Мы поможем в написании вашей работы!