Условие параллельности двух плоскостей

Расстояние от точки до плоскости.

Пусть задана точка точку М(х0,у0,z0) и плоскость Q, заданная уравнением Ах+Ву+Сz+D=0. Расстояние d от точки М0 до плоскости Q находится по формуле:

. (4.10)

Если плоскость Q задана уравнением, то расстояние d от точки М0 до плоскости Q может быть найдено по формуле:

. (4.11)

§5.Прямая и плоскость пространстве.

Уравнение прямой в пространстве.

1).Пусть дана какая-либо прямая L в пространстве.Положение ее определяется направляющим вектором прямой : если взять точку М0(х0,у0,z0) на прямой,то вектором является вектор,параллельный этой прямой.Возьмем на прямой L произвольную точку М(х,у,z),обозначимрадиус-векторы точек М0 и М через и соответственно.Три вектора , ,связаны между собой соотношением 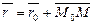. (5.1)

Вектор ,лежащий на прямой L, параллелен направляющему вектору ,

поэтому ,где t - скалярный множитель,называемый параметром, может принимать различные значения в зависимости от положения точки М на прямой.

Уравнение можно записать в виде:

. (5.2)

Полученное уравнение называется векторным уравнением прямой.

2).Если заметить,что , , , то векторное уравнение прямой принимает вид:

. (5.3)

Отсюда вытекает следующие равенства:

, (5.4)

которые называются параметрическими уравнениями прямой в пространстве.

3). Пусть -направляющий вектор прямой L и М0(х0,у0,z0) – точка,лежащая на этой прямой.Вектор ,соединяющий точку М0 с произвольной точкой М(х,у,z) прямой L,параллелен вектору .Поэтому координаты вектора

и вектора пропорциональны:

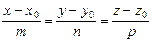- (5.5)

уравнение называется каноническим уравнением прямой в прстранстве.

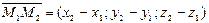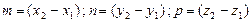4).Если прямая L проходит через две точки М1(х1,у1,z1) и М2(х2,у2,z2), то в качестве направляющего вектора можно взять вектор , т.е. ,следовательно .Поскольку прямая проходит через точку М1(х1,у1,z1), то согласно уравнениям (5.5),уравнения прямой L

имеют вид: . (5.6)

Уравнения (5.6) называются уравнениями прямой,проходящими через две данные точки.

5). Прямую в пространстве можно задать как линию пересечения двух непараллельных плоскостей.Рассмотрим систему уравнений

. (5.7)

Каждое из этих уравнение определяет плоскость.Если плоскости не параллельны,то система определяет прямую L как геометрическое мести точек пространства,координаты которых удовлетворяют каждому из уравнений системы.

Уравнения (5.7) называются общими уравнениями прямой.

ПРИМЕР. Написать канонические уравнения прямой L,заданной уравнениями

.

Пусть z=0 и решим систему .Найдем точку М1(-2,1,0).

Пусть у=0,тогда решим систему 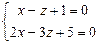,найдем вторую точку М2(2,0,3), принадлежащую прямой L. Тогда уравнение прямой,проходящей через две точки имеет вид (используем уравнение 5.6): .

Прямая и плоскость пространстве.

Основные задачи.

Угол между прямой и плоскостью.Условия параллельности и

перпендикулярности прямой и плоскости.

Пусть плоскость Q задана уравнением Ах+Ву+Сz+D=0,а прямая L уравнениями .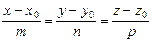

Определение. Углом между прямой и плоскостью называется любой из двух смежных углов,образованных прямой и ее проекцией на плоскость.Пусть φ-угол между плоскостью Q и прямой L, а через θ-угол между векторами

.

φ

пл.Q

Рис.1

Тогда , sinφ=sin(π/2-θ)=cosθ. Поскольку sinφ≥0, то имеем

.

Если прямая L параллельна плоскости Q, то векторы перпендикулярны и , т.е.

является условием перпендикулярности прямой к плоскости.

Если прямая L перпендикулярна плоскости Q, то векторы параллельны и

являются условиями перпендикулярности прямой и плоскости.

Пересечение прямой с плоскостью.Условие принадлежности

прямой плоскости.

Пусть дана прямая 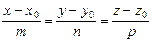и плоскость Ах+Ву+Сz+D=0. Требуется найти точку пересечения данных прямой и плоскости.Для этого надо решить систему уравнений,это сделать проще,если записать уравнение прямой в параметрическом виде:

.

Подставив эти выражения для х,у,z в уравнение плоскости,получаем уравнение

или . (5.8)

Если прямая L не параллельна плоскости,т.е. если ,тогда

.

найдем координаты точки пересечения прямой с плоскостью,подставив найденное значение t в параметрические уравнения прямой.

Теперь рассмотрим случай,когда :

1).если Ах0+Ву0+Сz0+D≠0,тогда прямая L параллельна плоскости и пересекать ее не

будет – уравнекние (5.8) решения не имеет,поскольку принимает вид

0·t+F=0,где F≠0;

2). если Ах0+Ву0+Сz0+D=0,то уравнение (5.8) имеет вид t·0+0=0; данном

уравнению удовлетворяет любое значение t, любая точка прямой является точкой

пересечения прямой и плоскости.Это говорит о том,что прямая лежит в плоскости.

Таким образом,одновременное выполнение равенств

является условием принадлежности прямой и плоскости.

Глава 4.ВВЕДЕНИЕ В АНАЛИЗ.

§1.Множества.Действительные числа.

1.1.Основные понятия.

Под множеством понимают совокупность некоторых объектов, объединенных по какому-либо признаку.Понятие множества является одним из основных неопределяемых понятий математики.Так можно говорить о множестве студентов института,о множестве всех натуральных чисел и т.д.

Объекты,составляющие множество,называются элементами.

Множество обозначается: А,В,…,Х,Y,…, а элементы- а,в,…,х,у,…

Принадлежность элемента х множеству Х обозначается: ;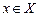

запись или означает,что элемент х не принадлежит множеству Х.

Множество,не содержащее ни одного элемента,называется пустым, обозначается символом Ø.

Элементы множества записываются в фигурных скобках: или

указывается общее свойство,которым обладают все элементы данного множества: .

Множество А называется подмножеством множества В,если каждый элемент множества А является элементом множества В,символически:или .

Множества А и В равны или совпадают,если состоят из одних и тех же элементов,пишут А=В,если и .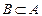

Объединением или суммой множеств А и В называется множество,состоящее из элементов,каждый из которых принадлежит хотя бы одному из множеств.Обозначается: 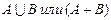,кратко: .

Пересечением или произведением множеств А и В называется множество, состоящее из элементов,каждый из которых принадлежит множеству А и множеству В. Обозначается: ,кратко: .

Для сокращения записей используются простейшие логические символы:

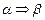- означает «из предложения α следует предложение β»;

- «предложения α и β равносильны»;

- означает «для любого», «для всякого»;

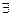- «существует», «найдется»;

: - «имеет место», «такое что»;

- «соответствие».

Например: означает: «для всякого элемента имеет место предложение α.

1.2.Числовые интервалы.Окрестность точки.

Пусть а и b – действительные числа,причем а < b.

Числовыми интервалами(промежутками) называются подмножества всех действительных чисел,имеющих вид:

- отрезок(сегмент,замкнутый промежуток);

- интервал(открытый промежуток);

;- полуоткрытые интервалы(или полуоткрытые отрезки);

; ;

; ;

- бесконечные интервалы(промежутки).

Пусть - любое действительное число(точка на оси ОХ).

Определение. Окрестностью точки называется любой интервал (а,b), содержащий точку .В частности,интервал ,где ε>0, называется ε-окрестностью точки ,число называется цнтром, число ε-радиусом.

ε ε

х

Рис.1

Если ,то выполняется неравенство 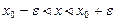или . Выполнение последнего неравенства означает попадание точки х

в ε-окрестность точки .

§2.Функция.

Пусть даны два непустых множества Х,У.

Определение. Соответствие f,которое каждому элементу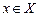сопоставляет один и только один элемент ,называется функцией.

Обозначается: у=f(х), 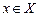или f: Х→У.

Множество Х называется областью определения функции f и обозначается D(f). Множество называется множеством значений функции f и обозначается Е(f).

Определение. Графиком функции у=f(х) называется множество всех точек плоскости Оху, для каждой из которых х является значением аргумента,а у – соответствующим значением функции.

Для задания функции необходимо указать правило,,позволяющее по значению х

определять соответствующее значение аргумента у.

Способы задания функции.

1). Аналитический способ: функция задается в виде одной или нескольких формул или уравнений.

Аналитический способ задания функции является наиболее совершенным,так как к нему приложены методы математического анализа,позволяющие полностью исследовать функцию у=f(х).

ПРИМЕР. а). ; в). ; с).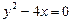

2). Графический способ: задается график функции.

Преимуществом графического задания функции является его наглядность, недостатком-его неточность.

3). Табличный способ: функция задается таблицей ряда значений аргумента и соответствующих значений функции.Например,таблицы значений тригонометрических функций,логарифмические таблицы.

Основные характеристики функции.

1). Четность. Функция у=f(х),определенная на множестве D,называется четной, если 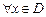выполняются условия ;

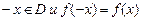нечетной, если 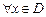выполняются условия .

График четной функции симметричен относительно оси Оу, а нечетной- относительно начала координат.

2). Монотонность. Пусть у=f(х) определена на множестве D и ,при чем .Тогда функция называется:

возрастающей, если ,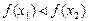

неубывающей, если ,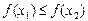

убывающей, если ,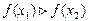

невозрастающей, если .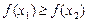

3). Ограниченность. Функцию у=f(х),определенную на множестве D называют ограниченной,если .

4). Периодичность. Функцию у=f(х),определенную на множестве D называют периодической на этом множестве,если .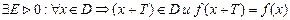

Число Т называют периодом функции. Если Т -период,то числа m∙T также будут ее периодами,где m=±1,±2,...

Например,функции у=sinx,cosx,tgx – периодические функции.

Сложная функция.

Определение. Пусть у=f(и) определена на множестве D, функция и=φ(х) – на множестве , при чем для 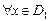.Т.е. на множестве определена функция

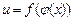,которая называется сложной функцией от х ( или суперпозицией заданных функций, или функцией от функции).

Переменную 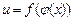называют промежуточным аргументом сложной функции.

Например, есть суперпозиция двух функций и .

Основные элементарные функции.

1). Показательная функция ;

2). Степенная функция ;

3). Логарифмическая функция ;

4). Тригонометрические функции ;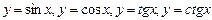

5). Обратные тригонометрические функции .

Определение. Элементарной функцией называется функция,задаваемая одной формулой,составленной из основных элементарных функций и постоянных с помощью конечного числа арифметических операций и операций взятия функции от функции.

ПРИМЕР. .

§3.Последовательности.

3.1.Числовая последовательность.

Определение. Числовой последовательностью Х1, Х2, Х3,… Хn,… понимается функция Хn = f (n),

заданная на множестве N натуральных чисел.

Кратко последовательность обозначается в виде {x_n} или Хn, n € N.

Число Х1 называется первым элементом последовательности, Х2 - вторым, …

Хn – общим или n- м элементом последовательности.

Чаще всего последовательность задается формулой общего элемента, которая позволяет вычислить любой элемент последовательности по номеру n.

ПРИМЕРЫ:

Общий элемент a_n: Первые элементы: (Х10) Десятый элемент:

1). a_n= 1,

2). a_n=3+2(n-1) 3,5,7,9,11... 21

3). a_n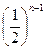=3 3,

4). a_n=2+(0,1) ⁿ 2,1; 2,01; 2,001; 2,0001; 2,00001... 2,0000000001

5). a_n=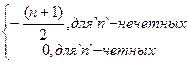 -1,0,-2,0,-3... 0

6). a_n=2n(-1)ⁿ+1 -1,5,-5,9... 21

7). a_n=4 4,4,4,4,4... 4

8). a_n=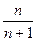

Ограниченной последовательностью называется

последовательность {х_n} |х_n| ≤L или

- L ≤х_n≤L.

В противном случае последовательность называется неограниченной:

: |х_nه| >M

Последовательность {х_n} ограничена сверху(снизу), если

х_n ≤L (х_n≥l)

Ограниченные последовательности: 1,3,4,7,8.

Неограниченные: 2,6.

ПОСЛЕДОВАТЕЛЬНОСТИограниченые сверху(снизу) 2,5

Возможно также определить последовательность как функцию.

(Вспомним определение функции у=f(х):

соответствие f, которое каждому элементу х €Х сопоставляет один и только

один элемент у €У,где Х- область определения функции f).

ПРИМЕР: последовательность имеет элементом

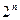
По определению последовательность есть функция : для всех

n целых позитивных.Графически (при бесконечно возрастающей):

8.

5

4.

2.

1 .....

1 2 3 4 5

Рис.2

Монотонные последовательности.

Возрастающая последовательность:

{u_n}, возрастает,если u_n+1>u_n, n Є IN u_n+1-u_n>0, n ЄIN_.

Убывающая последовательность:

{u_n}, убывает если u_n+1<u_n, n ЄIN u_n+1-u_n<0, n ЄIN.

Немонотонной называется последовательность,элементы которой ни возрастают,

ни убывают,например {(-1)^n-1} → {1,-1,1,-1,…}.( 3,5,6).

Если все элементы последовательности {x_n} равны одному и тому же

числу С, то ее называют постоянной. (N 7).

Другой способ задания числовых последовательностей - рекуррентный способ.

В нем задается начальный элемент x₁ (первый член последовательности) и правило определения n -го элемента по (n -1)- му:

x_{n = f (}x_{n -1).}

Таким образом x_{2 = f (}x_1), x_{3 = f (}x_{2) и т.д.} При таком способе задания последова- тельности для определения 50-го члена надо сначала подсчитать все 49 предыдущих.

3.2.Предел числовой последовательности.

Определение. Число a называется пределом последовательности {x_n},если:

для любого положительного числа ε найдется такое натуральное число N

что при всех выполняется неравенство . (3.1)

Кратко: : .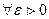

Пишем или 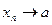и говорят, что последовательность {x_n}

(или переменная x_n пробегающая последовательность x_1, x_2, x_3,…)

имеет предел, равный числу а (или x_n стремится к а).

Последовательности,указанные ранее имеют следующие пределы:

1). a_n= 1, =0

2). a_n=4+3(n-1) 4,7,10,13,16... =

3). a_n=3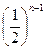 3, =0

4). a_n=2+(0,1)ⁿ 2,1; 2,01; 2,001; 2,0001; 2,00001... =2

5). a_n=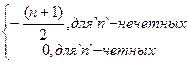 -1,0,-2,0,-3... -

6). a_n=n(-1)ⁿ+1 0,3,-2,5... -

7). a_n=4 4,4,4,4,4... =4

ПРИМЕР. Доказать,что lim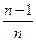=1.

По определению число 1 будет пределом последовательности

Хn = 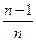, n € N,если найдется натуральное число N, такое, что для всех выполняется неравенство .

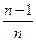| - 1 |<ε.,т.е. () <ε

Оно справедливо для всех n>(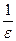), т.е. для всех n> N=[],

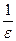где [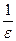]- целая часть числа (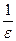), (целая часть числа х,обозначаемая [х],

есть наибольшее целое число,не превосходящее х: так [3]=3, [5,2]= 5.

Если ε>1, то в качестве N можно взять [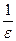]+1.

Итак, 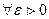указано соответствующее значение N. Это и доказывает, что lim[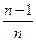]=1.

Заметим,что число N зависит от ε, так,

если ε=(), то N=[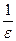]= [1/(326)]= [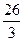]= [8,66…]=8.

ε=0,001,то N=[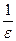]= [1/(11000)]= [1000]= 1000.Поэтому иногда записывают N= N(ε).

Геометрический смысл определения предела числовой последовательности.

Неравенство (3.1) равносильно неравенствам -ε<x_n -а <ε или а-ε< x_n <ε +а,

которые показывают что элемент x_n находится в ε -окрестности точки а.

О x_n

. (| |

Дата добавления: 2014-01-15