Получаем

.

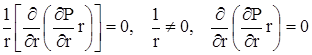Это и есть дифференциальное уравнение Лапласа в полярных координатах для установившегося плоскорадиального течения несжимаемой жидкости по закону Дарси.

Дважды проинтегрировав дифференциальное уравнение, получаем

.

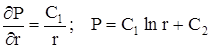Постоянные интегрирования С₁, С₂ находим как обычно из граничных условий Р = Р_c при r = r_c; Р = Р_к при r = R_k.

Подставляя граничные условия, получаем систему уравнений для нахождения С₁, С₂:

.

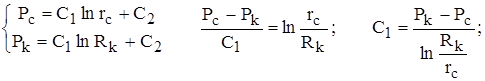
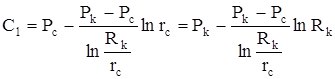Подставляя найденные значения С₁ и С₂ в решение, получим зависимость давления от координаты r в плоскорадиальном потоке.

.

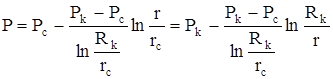Находим градиент давления

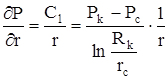
и используем его для нахождения скорости фильтрации

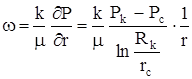
и дебита

,

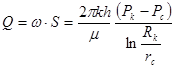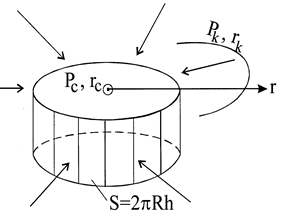
где: S = 2prh – поверхность фильтрации (боковая поверхность цилиндра радиуса r и высотой h) (рис. 11.3).

Формула 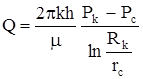- называется формулой Дюпюи.

	Рис. 11.3.

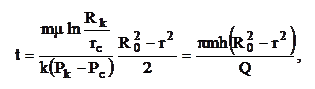
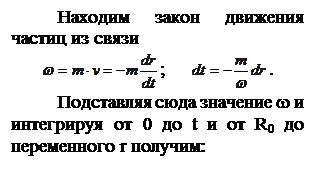
где: R₀ – начальное положение частицы в момент t = 0 и r – текущее положение в момент t.

Если в эту формулу подставить вместо R₀ ®R_к, а вместо r ® r_c, то получим время Т отбора всей жидкости, находящейся в пласте

.

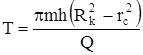Находим средневзвешенное по объему порового пространства пластовое давление

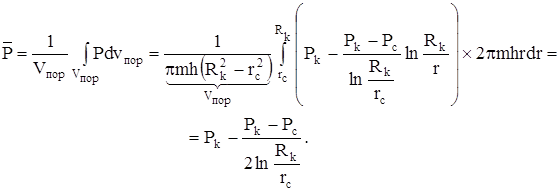
Прокомментируем некоторые результаты.

Дебит скважины пропорционален депрессии DР (разнице давлений в пласте и на забое работающей скважины) и одинаков через любую цилиндрическую поверхность, т.е. не зависит от r.

Отношение объемного дебита скважины к DР называется коэффициентом продуктивности

;

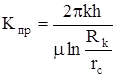_.Через этот коэффициент дебит скважины выражается уравнением

Q=K_прDP, которое называется индикаторной диаграммой. На ней коэффициент продуктивности определяется как тангенс угла наклона прямой к оси DP (tg j = K_пр). На практике индикаторную диаграмму строят по данным испытания скважины, путем получения притоков нефти при различных депрессиях.

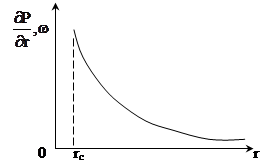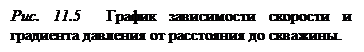
Градиент давления и скорости фильтрации ведут себя одинаково и резко возрастают при приближении к скважине (рис. 11.5).

Логарифмическая кривая давления, вращение которой вокруг скважины образует поверхность, называется воронкой депрессии. Основная часть депрессии образуется в призабойной зоне, параметры которой сильно влияют на дебит скважины (рис. 11.6).

Рис. 11.6 Воронка дисперсии (а) и гидродинамическое поле (б)

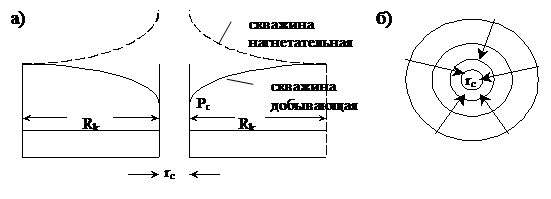Гидродинамическое поле плоскорадиального потока описывается семействами изобар и линий тока. Изобара представляет окружности, поскольку, Р ~ 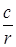уравнение окружности. Линии тока – прямые, совпадающие с радиусами. Все выведенные формулы с заменой (Р_к – Р_с) на (Р_с – Р_к) справедливы для нагнетательных скважин.

3.5.3 Радиально-сферический фильтрационный поток

Дата добавления: 2014-01-15