
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Алгебраїчні рівняння
|
|
|
|
Відповідь
28. 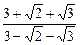 .
. 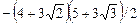
29. 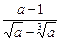 .
. 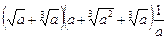
30. 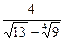 .
. 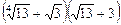
Обчислити без калькулятора (31 — 36). Відповідь
31. 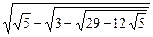 . 1
. 1
32. 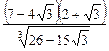 . 1
. 1
33. 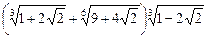 .
. 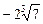
34. 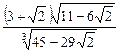 . 7
. 7
35. 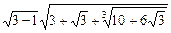 . 2
. 2
36. 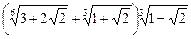 .
. 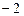
ЛЕКЦІЯ
 |
4.1. Загальні відомості про рівняння
Рівнянням називається рівність, яка містить змінні величини і виконується лише при деяких значеннях цих змінних.
Нехай 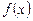 — функція, визначена при дійсних значеннях
— функція, визначена при дійсних значеннях 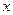 , яка набуває лише дійсних значень. Якщо
, яка набуває лише дійсних значень. Якщо 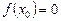 , то число
, то число 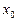 називається нулем функції
називається нулем функції 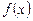 або коренем рівняння
або коренем рівняння
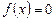 . (1)
. (1)
Розв’язати рівняння (1) означає знайти всі його корені і довести відсутність інших корнів, крім знайдених.
Два рівняння 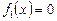 ,
, 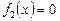 називаються еквівалентними, або рівносильними, якщо множини їхніх розв’язків збігаються.
називаються еквівалентними, або рівносильними, якщо множини їхніх розв’язків збігаються.
Процес розв’язування рівняння (1) полягає в перетворенні його до такого вигляду, який дає змогу легко знайти його корені. Під час перетворення рівняння (1) область його визначення (область допустимих значень — ОДЗ) може змінюватися, а через це можлива поява сторонніх коренів або втрата коренів.
Приклад. Розв’язати ірраціональне рівняння
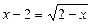
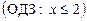 . (2)
. (2)
Ø Піднесемо обидві дві частини рівняння до квадрата:
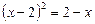 ,
, 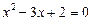 ,
, 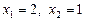 .
.
Унаслідок піднесення обох частин рівняння до квадрата ОДЗ розширюється і з’являється сторонній корінь 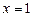 , який є коренем рівняння
, який є коренем рівняння
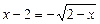 . (3)
. (3)
Підносячи до квадрата обидві частини рівняння (3), дістаємо рівняння 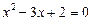 .
.
Приклад. Розв’язати алгебраїчне рівняння
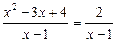 .
.
Ø Прирівнюючи чисельники, маємо:
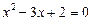 ,
, 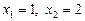 .
.
Значення 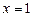 не є розв’язком вихідного рівняння.
не є розв’язком вихідного рівняння.
4.2. Рівняння першого степеня
з одним невідомим
Розглянемо рівняння першого степеня з параметрами
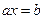 . (1)
. (1)
1. При 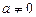 рівняння має один розв’язок
рівняння має один розв’язок 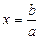 .
.
2. При 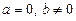 рівняння не має розв’язків.
рівняння не має розв’язків.
3. При 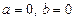 кожне значення
кожне значення 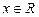 є розв’язком рівняння. Розв’язок рівняння не єдиний. Рівняння має безліч розв’язків.
є розв’язком рівняння. Розв’язок рівняння не єдиний. Рівняння має безліч розв’язків.
Приклад. Знайти розв’язок лінійного рівняння
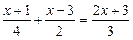 .
.
Ø Зводимо рівняння до вигляду
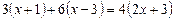 ,
, 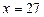 .
.
Приклад. Розв’язати лінійне рівняння
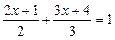 .
.
Ø Дане рівняння зводитися до вигляду
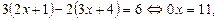 x Î Æ.
x Î Æ.
Приклад. Розв’язати лінійне рівняння
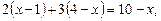
Ø 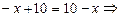
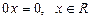 .
.
Приклад. Розв’язати лінійне рівняння
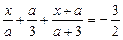 .
.
Ø При 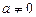 ,
, 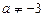 рівняння перетворюється до вигляду
рівняння перетворюється до вигляду
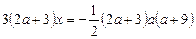 .
.
1. Якщо 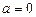 або
або 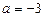 , то рівняння не має розв’язків.
, то рівняння не має розв’язків.
2. Якщо 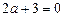 , то
, то 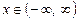 , тобто
, тобто 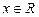 .
.
3. Якщо 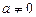 ,
, 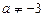 ,
, 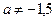 , то
, то 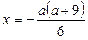 .
.
Приклад. Знайти розв’язок рівняння
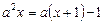 .
.
Ø Рівняння перетворюється до вигляду 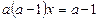 .
.
1. Якщо 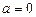 , то рівняння не має розв’язків.
, то рівняння не має розв’язків.
2. Якщо  , то
, то 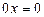 ,
, 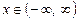 .
.
3. Якщо 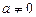 ,
, 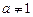 , то
, то 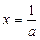 .
.
Часто систему лінійних алгебраїчних рівнянь можна звести до одного лінійного рівняння виду 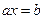 .
.
Приклад. Знайти розв’язок системи лінійних рівнянь
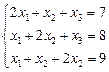 .
.
Ø З першого рівняння знаходимо 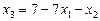 і підставляємо в друге та третє рівняння. Дістаємо систему
і підставляємо в друге та третє рівняння. Дістаємо систему
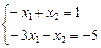 .
.
З першого рівняння знаходимо 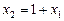 і підставляємо в друге рівняння. Дістаємо одне рівняння з одним невідомим
і підставляємо в друге рівняння. Дістаємо одне рівняння з одним невідомим 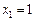 . З попередніх рівнянь знаходимо
. З попередніх рівнянь знаходимо 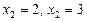 .
.
Аналогічно виключаються невідомі із системи лінійних алгебраїчних рівнянь з параметрами.
Приклад. Знайти значення параметра b, при якому система лінійних рівнянь
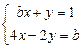
має нескінченну множину розв’язків.
Ø Виключаючи невідоме 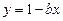 , дістаємо рівняння
, дістаємо рівняння
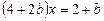 .
.
При 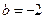 це рівняння, а отже, і вихідна система лінійних рівнянь має нескінченну множину розв’язків.
це рівняння, а отже, і вихідна система лінійних рівнянь має нескінченну множину розв’язків.
Приклад. Знайти значення параметра 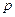 , при якому система рівнянь
, при якому система рівнянь
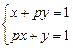
не має розв’язків.
Ø Виключаючи невідоме 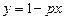 , приходимо до рівняння першого степеня з одним невідомим
, приходимо до рівняння першого степеня з одним невідомим
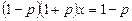 .
.
При 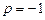 це рівняння, а отже, і вихідна система рівнянь не має розв’язків.
це рівняння, а отже, і вихідна система рівнянь не має розв’язків.
Приклад. Знайти значення параметра  , яке задовольняє таку умову: для будь-якого дійсного значення параметра
, яке задовольняє таку умову: для будь-якого дійсного значення параметра  знайдеться хоча б одне значення параметра
знайдеться хоча б одне значення параметра 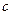 , таке що задана система
, таке що задана система
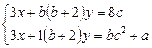
має принаймні один розв’язок.
Ø Виключивши із системи рівнянь невідоме 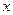 , дістанемо лінійне рівняння
, дістанемо лінійне рівняння
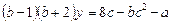 .
.
Якщо 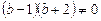 , то це рівняння має розв’язок при будь-якому значенні
, то це рівняння має розв’язок при будь-якому значенні 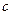 . При
. При 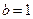 або
або 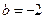 коефіцієнт при
коефіцієнт при 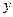 у ньому перетворюється на нуль. Щоб це рівняння мало розв’язок, необхідне виконання умов
у ньому перетворюється на нуль. Щоб це рівняння мало розв’язок, необхідне виконання умов
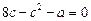 ,
, 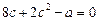 .
.
Дістали два квадратних рівняння відносно с, розв’язки яких існують за умови невід’ємності їхніх дискримінантів:
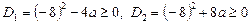
Звідси знаходимо значення параметра 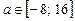 .
.
Приклад. Знайти умови, за яких існують розв’язки системи лінійних рівнянь
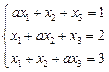
Ø Додаючи почленно рівняння системи, дістаємо:
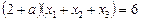 ,
, 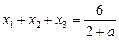 .
.
Послідовно віднімаючи від цього рівняння кожне з рівнянь системи, знаходимо розв’язки системи, виражені через параметр а:
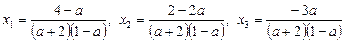 .
.
Розв’язки системи рівнянь існують, якщо 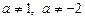 .
.
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 2947; Нарушение авторских прав?; Мы поможем в написании вашей работы!