Відповідь

1. ;

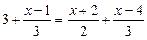
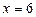2. ;

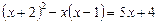
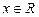3. ;

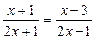
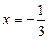4. ;

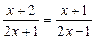
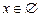5. ;

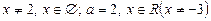6. ;

7. ;

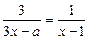
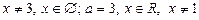8. ;

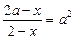
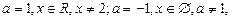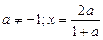
9.

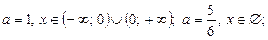
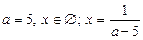при ;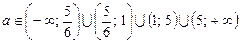

10. При яких значеннях параметра для довільного дійсного значення знайдеться хоча б одне дійсне значення параметра 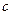, таке що задана система рівнянь

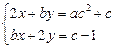
матиме принаймні один розв’язок.

4.3. Рівняння другого степеня
з одним невідомим

Алгебраїчне рівняння другого степеня з одним невідомим

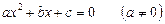(1)

називається також квадратним рівнянням.

Рівняння виду

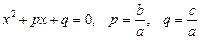
називається зведеним квадратним рівнянням і має розв’язок

.

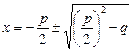Для рівняння (1) розв’язок можна подати у вигляді

.

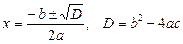Для коренів 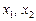зведеного квадратного рівняння справджується формула Вієта

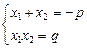
Цей результат випливає з тотожності

.

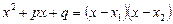Корені квадратного рівняння (1) дійсні і різні при 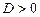, крат­ні при 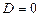і не є дійсними при 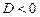. Якщо 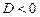, то многочлен

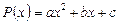
з дійсними коефіцієнтами 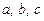набуває значень лише одного знака. При 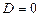многочлен 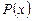набуває значень одного знака, за винятком однієї точки — кратного кореня рівняння (1), де многочлен 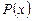набуває нульового значення.

Приклад. Знайти розв’язок рівняння

.

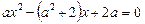Ø При 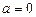рівняння має один розв’язок .

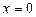При 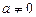знаходимо дискримінант

,

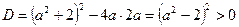а отже, рівняння має два розв’язки

.

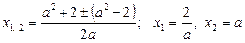Приклад. Розв’язати рівняння з параметром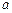

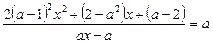, якщо , .

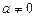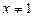Ø Виконавши відповідні перетворення, дістанемо квадратне рівняння

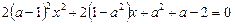, (2)

дискримінант якого

.

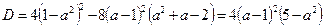При ліва частина рівняння (2) тотожно дорівнює нулю, а тому його розв’язком є будь-яке значення .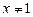

При 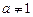обидві частини рівняння (2) можна поділити на 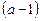, знайшовши два корені:

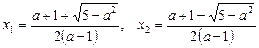. (3)

За умови 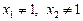маємо

.

Розв’язавши рівняння 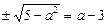при 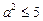, дістанемо розв’язок 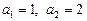. Остаточно доходимо таких висновків.

1. При 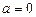рівняння не має розв’язків.

2. При рівняння має довільний розв’язок .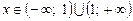

3. При 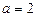рівняння має єдиний розв’язок .

4. При 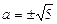рівняння має дворазові розв’язки .

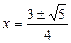5. При 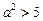рівняння має комплексні розв’язки.

6. При 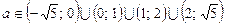рівняння має два різ­ні розв’язки виду (3).

Приклад. Розв’язати рівняння

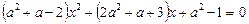з параметром .

Ø Якщо 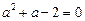, то дане рівняння стає лінійним. Розв’язуючи рівняння 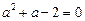, знаходимо .

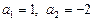При рівняння має єдиний розв’язок .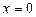

При 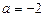рівняння має розв’язок .

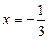При 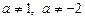знаходимо дискримінант

,

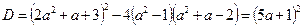а далі й корені рівняння

.

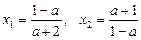Приклад. Розв’язати рівняння

.

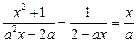Ø Передусім доходимо висновку, що .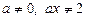

При цьому рівняння зводиться до вигляду

.

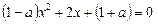Знаходимо дискримінант цього рівняння

.

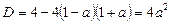При 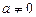виконуються умов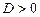и . При 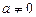, 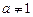знаходимо розв’язок рівняння

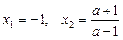. (4)

Якщо , то рівняння має єдиний розв’язок 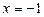. Перевіримо виконання умови 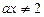, яка набирає вигляду нерівностей

.

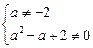Остаточно доходимо таких висновків.

1. Якщо , то рівняння має єдиний розв’язок .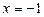

2. При 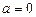рівняння розв’язків не має.

3. При 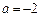рівняння має єдиний розв’язок .

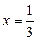4. Якщо 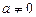, , 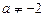то рівняння має два розв’язки виду (4).

4.4. Задачі на використання
властивостей дискримінанта

Якщо дискримінант 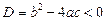, то квадратне рівняння

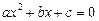
не має дійсних коренів. Через це квадратний тричлен

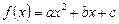
не змінює свого знака при 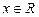і має знак коефіцієнта 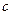або коефіцієнта .

Приклад. Для яких значень параметра 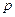виконується нерівність

?

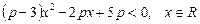Ø Необхідною і достатньою умовою правильності нерівності є виконання системи умов

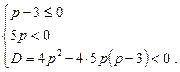
Розв’язуючи цю систему нерівностей, знаходимо відповідь: .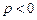

Приклад. При яких значеннях параметра нерівність

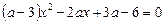
виконується для будь-якого значення ?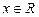

Ø Приходимо до системи нерівностей

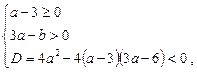
яка має розв’язок .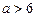

Приклад. Знайти всі значення параметра , при яких нерівність

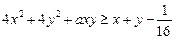
виконується для пари будь-яких чисел 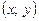, таких що .

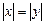Ø Якщ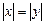о , то 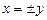. Приходимо до системи нерів-
ностей

яку можна записати у вигляді

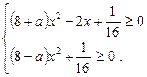
Приходимо до системи нерівностей для параметра :

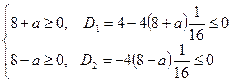
Ця система має розв’язок .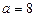

4.5. Використання формул Вієта

Приклад. Знайти значення параметра , при яких відношення коренів рівняння

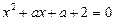
дорівнює 2.

Ø Маємо систему рівнянь

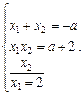
Оскільки шукаємо тільки значення параметра , то виключаємо невідомі 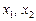. Маємо рівняння:

.

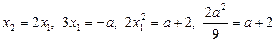Останнє рівняння має розв’язки , .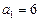

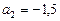При 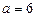маємо 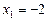, , 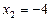а при , .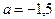

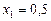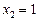Приклад. Знайти добуток значень параметра , при яких сума коренів рівняння

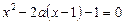
дорівнює сумі їхніх квадратів.

Ø Скориставшись формулами Вієта, дістанемо систему

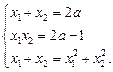
Останнє рівняння можна записати у вигляді

.

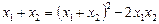Виключаючи 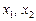, дістаємо рівняння для

.

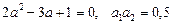Приклад. Знайти ціле значення параметра 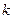, при якому рівняння

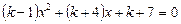
має рівні між собою корені.

Ø Квадратне рівняння має рівні між собою корені, якщо його дискримінант дорівнює нулю. Розв’яжемо рівняння

,

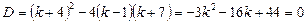звідки 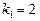, 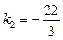. Значення 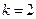шукане.

Приклад. Знайти суму кубів коренів рівняння

.

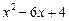Ø Можна знайти корені рівняння 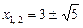і обчислити суму кубів коренів:

.

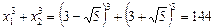Таку саму відповідь можна дістати за допомогою формул Вієта:

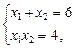
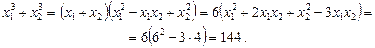
Функція 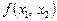називається симетричною, якщо вона не змінюється внаслідок довільного перестановлення аргументів, тобто .

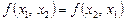Коефіцієнти зведеного квадратного рівняння

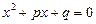
є симетричними функціями від коренів рівняння.

Довільну симетричну функцію 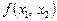завжди можна подати через основні симетричні функції 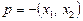, 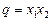. Це й було виконано в попередньому прикладі.

Приклад. При яких значеннях параметра 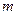сума квадратів коренів рівняння

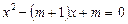
буде мінімальною?

Ø Використовуючи формули Вієта, дістаємо:

.

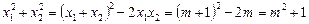Знаходимо дискримінант рівняння

.

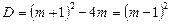Оскільки при довільних значеннях параметра 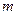виконується нерівність 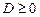, то на значення параметра 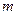обмежень немає. Сума квадратів коренів набуває найменшого значення, що дорівнює 1, при .

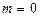Приклад. При якому значенні параметра 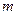сума квадратів коренів рівняння

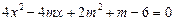
набуває найменшого значення?

Ø Знаходимо дискримінант рівняння (1):

.

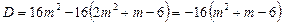З умови 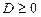знаходимо, що рівняння (1) має розв’язок лише при 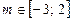. Знаходимо суму квадратів коренів рівняння (1) за формулами Вієта:

.

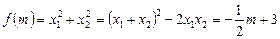Найменшого значення лінійна функція 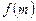може набувати лише на кінці відрізка .

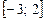Оскільки 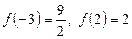, то 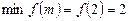досягається при .

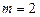Приклад. При яких значеннях параметра рівняння

,

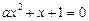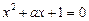
мають спільний корінь?

Ø Запишемо рівняння Вієта

,

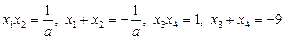а далі візьмемо 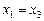. Крім значень 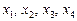дістаємо також 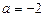. Рівняння

,

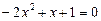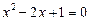
мають спільний корінь .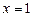

Ще один спосіб розв’язування прикладу полягає ось у чому.

Нехай 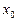— шуканий спільний корінь рівнянь. Маємо систему алгебраїчних рівнянь

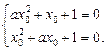(2)

Виключимо 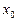, помноживши друге рівняння на і віднявши від першого рівняння. Дістанемо рівняння

.

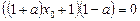При рівняння (2) не мають дійсних розв’язків.

Виключаючи 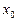, дістаємо рівняння для параметра :

, .

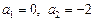При 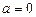рівняння (2) не мають спільного кореня. При 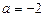рівняння (2) мають спільний корінь .

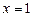Приклад. Знайти значення параметра , при якому один із коренів рівняння

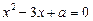(3)

утричі менший від одного з корнів рівняння

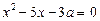. (4)

Ø Нехай 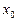— корінь рівняння (3), 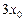— корінь рівняння (4). Маємо систему рівнянь

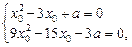
з якої знаходимо 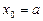. Підставляючи 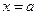в рівняння (3), діста­ємо рівняння для :

.

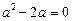При 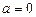рівняння (3) має корінь 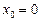, а рівняння (4) — корінь .

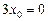При 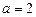рівняння (3) має корінь 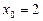, а рівняння (4) — корінь .

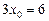4.6. Розміщення коренів
квадратного рівняння

З’ясуємо, як розміщуються на дійсній осі корені квадратного рівняння

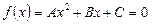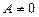, . (1)

З цією метою скористаємося тим, що графіком функції 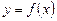є парабола, опукла вниз при 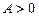і опукла вгору при .

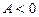Наведемо прості теореми стосовно розміщення коренів квадратного рівняння (1) на дійсній осі.

Теорема 1. Якщо 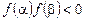, то на інтервал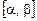і мі-
ститься один корінь рівняння (1).

Теорема 2. Якщо 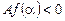, то точка 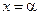лежить між коренями рівняння (1).

Теорема 3. Якщо 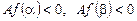, то відрізок 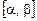лежить між коренями рівняння (1).

Теорема 4. Якщо 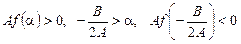, то корені рівняння (1) лежать на півосі .

Теорема 5. Якщо 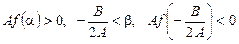, то корені рівняння (1) лежать на півосі .

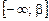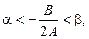
Теорема 6. Якщо 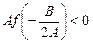, то корені рівняння (1) лежать на інтервалі .

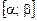Приклад. Знайти значення параметра , при яких два корені рівняння

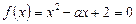
існують і належать інтервалу (0; 3).

Ø Графік функції 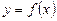має перетинати вісь Ох або дотикатися до неї в точках, розміщених праворуч від точки 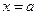. Тому дістаємо нерівності 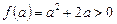, , , 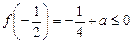які мають розв’язки .

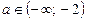Ще один спосіб розв’язування полягає у відшуканні найменшого кореня квадратного рівняння

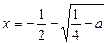
та розв’язуванні нерівності 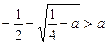, що також приводить до нерівності .

Приклад. Знайти значення параметра , при яких рівняння

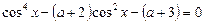
має розв’язок.

Ø Позначивши 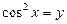, дістанемо квадратне рівняння

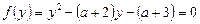. (2)

Вихідні рівняння мають розв’язки, якщо рівняння (2) має корінь 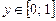. Застосуємо загальний метод розв’язування. Дискримінант рівняння (2).

.

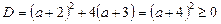Тому рівняння (2) при довільних значеннях параметра має дійсні розв’язки. Функція 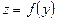досягає найменшого значення при .

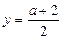Рівняння (2) матиме два розв’язки на відрізку [0; 1], якщо виконуватимуться нерівності

, , .

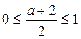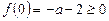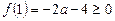Ці нерівності несумісні, оскільки не мають спільного розв’язку. Тому рівняння (2) не може мати двох коренів на відріз­ку [0; 1] при будь-якому значенні параметра .

Розглянемо всі інші можливості.

Якщо 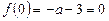, то рівняння (2) має корінь .

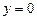Якщо 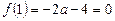, то рівняння (2) має один корінь на інтервалі (0; 1). Отже, оскільки при 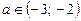рівняння (2) має корінь на інтервалі (0; 1), остаточно дістанемо, що при 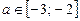рівняння (2) має корінь на відрізку [0; 1], а вихідне рівняння має дійсні розв’язки.

У даному прикладі можна було б відразу розв’язати рівняння (2):

.

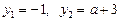Умова 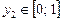приводить до нерівності .

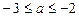Приклад. При яких значеннях параметра корені квадратного рівняння

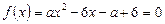
додатні?

Ø Знайдемо дискримінант рівняння

.

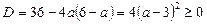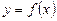Отже, корені рівняння існують при довільних значеннях параметра . Вершина параболи міститься точці 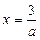. Для того щоб корені рівняння були додатніми, необхідно і достат­ньо, щоб виконувались нерівності

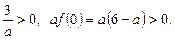
Звідси випливає, що корені квадратного рівняння додатні при .

У цьому прикладі можна знайти корні

, .

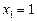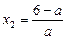З нерівності 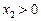випливає .

Дата добавления: 2014-01-11