История комплексных

Впервые, по-видимому, мнимые величины появились в известном труде «Великое искусство, или об алгебраических правилах» Кардано (1545), который счёл их непригодными к употреблению. Пользу мнимых величин, в частности, при решении кубического уравнения, в так называемом неприводимом случае (когда вещественные корни многочлена выражаются через кубические корни из мнимых величин), впервые оценил Бомбелли (1572). Он же дал некоторые простейшие правила действий с комплексными числами.

Выражения вида , появляющиеся при решении квадратных и кубических уравнений, стали называть «мнимыми» в XVI—XVII веках, однако даже для многих крупных ученых XVII века алгебраическая и геометрическая сущность мнимых величин представлялась неясной. Лейбниц, например, писал: «Дух божий нашёл тончайшую отдушину в этом чуде анализа, уроде из мира идей, двойственной сущности, находящейся между бытием и небытием, которую мы называем мнимым корнем из отрицательной единицы».^[5]

Долгое время было неясно, все ли операции над комплексными числами приводят к комплексным результатам, или, например, извлечение корня может привести к открытию какого-то нового типа чисел. Задача о выражении корней степени n из данного числа была решена в работах Муавра (1707) и Котса (1722).

Символ предложил Эйлер (1777, опубл. 1794), взявший для этого первую букву слова лат. imaginarius. Он же распространил все стандартные функции, включая логарифм, на комплексную область. Эйлер также высказал в 1751 году мысль об алгебраической замкнутости поля комплексных чисел. К такому же выводу пришел Д’Аламбер (1747), но первое строгое доказательство этого факта принадлежит Гауссу (1799). Гаусс и ввёл в широкое употребление термин «комплексное число» в 1831 году, хотя этот термин ранее использовал в том же смысле французский математик Лазар Карно в 1803 году.

Геометрическое истолкование комплексных чисел и действий над ними появилось впервые в работе Весселя (1799). Первые шаги в этом направлении были сделаны Валлисом (Англия) в 1685 году. Современное геометрическое представление, иногда называемое «диаграммой Аргана», вошло в обиход после опубликования в 1806-м и 1814-м годах работы Ж. Р. Аргана, повторявшей независимо выводы Весселя. Термины «модуль», «аргумент» и «сопряжённое число» ввёл Коши.

Арифметическая модель комплексных чисел как пар вещественных чисел была построена Гамильтоном (1837); это доказало непротиворечивость их свойств. Гамильтон предложил и обобщение комплексных чисел — кватернионы, алгебра которых некоммутативна

Операции над комплексными числами.

Сложение двух комплексных чисел 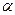= (а, b), 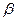= (с, d) определяется равенством

= (a + c, b + d) (1.1)

Применяя это определение к двум действительным числам а и c, найдем:

(а, 0) + (с, 0) = (а + с, 0) = a + с,

Операция сложения, будучи применена к действительным числам, дает в результате те же числа, какие получаются в ариф­метике действительных чисел,

Умножение двух комплексных чисел 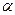и 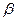определяется равенством
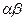= (ac - bd, ad + bc),(1.2)

Это определение, будучи применимо к двум действительным числам а и c, дает (а, 0) (с, 0) = (ас, 0) = ас, т. е. действие умножения не приводит к противоречию с арифметикой действительных чисел. Пользуясь определениями (1.1) и (1.2), легко проверить, что операции сложения и умножения комплексных чисел подчиняются известным пяти законам арифметики:

1) коммутативность сложения: = + ,

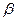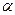2) коммутативность умножения: = ,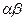

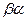3) ассоциативность сложения: + (,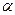

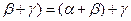4) ассоциативность умножения: ,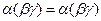

5) дистрибутивность умножения относительно сложения: .

В операциях с комплексными числами особую роль играет число, изображаемое парой (0, 1) и обозначаемое буквой i. Возводя эту пару в квадрат, что сводится к умножению ее на самое себя, по­лучаем в силу определения (1.2):

= (0,1)(0,1) = (-1,0) = -1,

т. е. = - 1, откуда берет свое начало обозначение i = 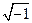. Символ i = 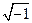предложил Л. Эйлер в 1777 г. Заметив это, всякое комплексное число можно записать так:

= (а, b) = (a, 0) + (0, b) = (a, 0) + (b,0)(0,1) = а + bi

т. е. всякое комплексное число = (а, b) может быть предста­влено в виде суммы действительного числа a и чисто мнимого числа bi.

Отсюда получаем алгебраическую форму записи комплексного числа

, где x = Re z, y = Im z.

Два комплексных числа, по определению, назы­ваются равными, если равны между собой их действительные части и равны их мнимые части.

Два комплексных числа, имеющих одну и ту же первую компо­ненту, но противоположные по знаку вторые компоненты, называются сопряженными и обозначаются так:

z = a + bi, 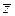= a – bi.

Как частный случай равенства (1.2) отметим закон умножения двух сопряженных чисел

z 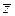= (a + bi)(a – bi) = .

В арифметике модулем сложения называется такое число, от при­бавления которого результат не меняется - число 0; аналогично 1 есть модуль умножения, т. е. число, от умножения на которое результат не меняется.

В области всех комплексных чисел имеется один модуль сложения — число 0 и один модуль умножения — число 1.

Пусть есть модуль сложения, т. е.

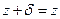, (1.3)

где z - произвольное комплексное число. Покажем, что такое число существует и притом единственное. Прибавляя к обеим частям ра­венства (1.3) число – z =(-1) z, получим: = 0.

Пусть, есть модуль умножения, т. е.

z = z, z 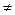0 (1.4)

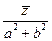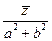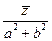Умножая обе части равенства на число, получим z = z.

Так как z 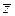= , то отсюда следует: = 1.

По определению произведение двух комплексных чисел есть нуль, если хотя бы один из сомножителей равен нулю. Справедливо и обратное положение: если произведение двух ком­плексных чисел равно нулю, то, по крайней мере, один из сомножи­телей есть нуль.

В самом деле, пусть z = 0, z 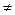0. Умножая обе части этого равенства на число 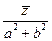, получим: = 0

Вычитание комплексных чисел опре­деляется как действие, обратное сложению. Разностью двух комплекс­ных чисел 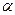= a + i b и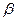 = с + i d называют, по определению, число z, удовлетворяющее равенству

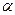+ z = 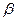(1.5)(1.5)

Покажем, что операция вычитания однозначно выполняется в об­ласти комплексных чисел. Прибавим к обеим частям равенства (1.5) число -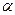, получим:

z =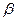+ (-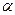) =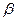- 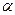= (c – a) + (d – b) i.

Деление комплексных чисел есть действие, обратное умножению. Так, под символом , по определению, понимают число z, удовле­творяющее равенству

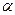
z = 1 (1.6)

Умножая обе части равенства (1.6) на число найдем: z == .

Таким образом, .

Деление, за исключением деления на нуль, всегда и притом однозначно выполняется в области комплексных чисел.

Равенства

(a + ib) + (c + id) = (a+c) + (b+d) i

(a - ib) + (c - id) = (a+c) - (b+d) i,

,

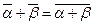(a + ib) (c + id) = (ас - bd) + (ad + bc) i,

(a - ib) (c - id) = (ас - bd) - (ad + bc) i,

.

, .

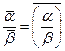показывают, что если в сумме (разности) или произведении (делении) двух комплексных чисел заменим числа сопряженными им числами, то в результате получим числа сопряженные.

В отличие от действительны чисел, комплексные числа (а не их модули) никогда нельзя соединять знаком неравенства.

Дата добавления: 2014-01-15