Множення матриць

План.

План.

1. Визначник, мінор, алгебраїне доповення.

2. Основні властивості визначників (*).

3. Методи обчислення визначників (**).

1.1 Визначник, мінор, алгебраїчне доповнення.

Розглянемо систему рівнянь, яка має п – рядків і п – невідомих:

Така система має числову характеристику, яка називається визначником (або детермінантом: det): 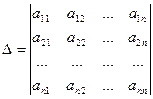. Даний визначник має порядок п.

Мінором визначника D порядку п називається визначник (п-1) порядку, який отримуємо в результаті викреслювання з визначника D і – того рядка і к – того стовпця. Позначають .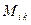

Приклад: ,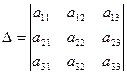

Алгебраїчним доповненням елемента 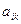називається величина : .

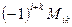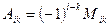Приклад: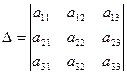

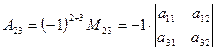
Значення визначника D дорівнює сумі добутків елементів якого – небудь стовпця (або рядка) на їх алгебраїчні доповнення:

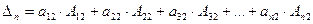(розклад за елементами другого стовпця).

Обчислимо визначник другого порядку: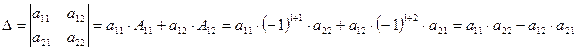

1.2 Основні властивості визначників.

1) значення визначника не зміниться, якщо його рядки замінити відповідними стовпцями;

2) якщо поміняти місцями два відповідних рядка визначника, то результат змінить знак на протилежний;

3) визначник з двома однаковими паралельними рядками дорівнює нулю;

4) якщо елементи деякого рядка (або стовпця) мають спільний множник, то його можна виносити за знак визначника;

5) якщо всі елементи деякого рядка дорівнюють нулю, то визначник дорівнює нулю

6) визначник, у якого елементи двох паралельних рядків пропорційні, дорівнює нулю;

7) визначник не зміниться, якщо до елементів якого – небудь стовпця (рядка) додати відповідні елементи іншого стовпця (рядка) помножені на одне і те ж число;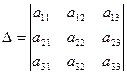

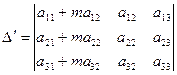
8) якщо кожний елемент якого – небудь стовпця є сумою двох доданків, то визначник дорівнює сумі двох визначників, у яких стовпцями є відповідні доданки, а решта збігається з стовпцями заданого визначника:

1.3 Методи обчислення визначників.

1. Визначники 3^го – порядку обчислюються за правилом Саррюса (правило трикутників).

2. Обчислення визначників (третього та вищих порядків) розкладанням за елементами і - рядка або j - стовпця.

Теорема: визначник дорівнює сумі добутків елементів якого – небудь рядка (стовпця)на їх алгебраїчні доповнення, тобт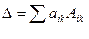о або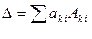

Розкладання визначника 4 – го порядку за елементами 2 – го рядка:

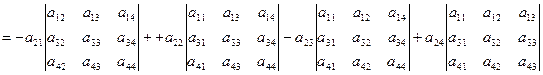
3. Обчислення визначників методом ефективного зниження порядку.

Використовуючи основні властивості визначників, обчислення визначника завжди можна звести до обчислення визначника (п-1)- го порядку, зробивши в якому – небудь рядку (стовпці) всі елементи рівні нулю, крім одного.

Приклад: 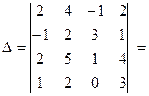зробимо нулі в третьому стовпці: для цього елементи першого і четвертого рядка залишаємо без зміни; елементи першого рядка множимо на 3 і додаємо до відповідних елементів другого рядка і записуємо в другому рядку; відповідні елементи першого і третього рядків додаємо і записуємо в третьому рядку =зробимо нулі в третьому рядку: для цього елементи першого стовпця залишаємо без зміни; елементи першого стовпця множимо на 2 і додаємо до відповідних елементів другого стовпця і записуємо в другому стовпці; елементи першого стовпця множимо на -3 і додаємо до відповідних елементів третього стовпця і записуємо в третьому стовпці

4. Метод зведення визначника до трикутного вигляду.

Використовуючи основні властивості визначників, обчислення визначника зводимо визначник до трикутного вигляду, тоді значення визначника дорівнює добутку його діагональних елементів.

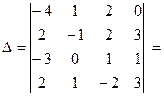поміняємо місцями перший та другий стовпці

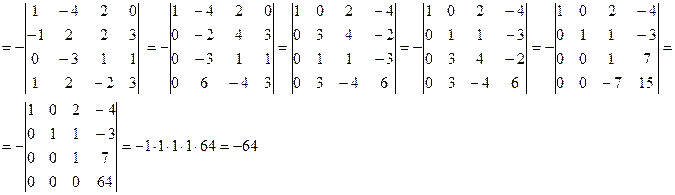
Контрольні запитання.

1. Що називається визначником, мінором визначника, алгебраїчним доповненням?

2. Назвіть основні властивості визначників?

3. Сформулюйте методи обчислення визначників і поясніть їх суть.

Лекція 2. Матриці. Дії з матрицями. Обернена матриця. Ранг матриці. Методи розв’язування систем лінійних рівнянь

4. Матриці.

5. Дії над матрицями (*).

6. Обернена матриця (*).

7. Методи розв’язування систем лінійних рівнянь (***).

8. Ранг матриці (*).

9. Однорідні системи (*).

2.1 Матриці.

В техніці дуже часто зустрічаються випадки, коли треба розв’язати систему рівнянь, яка містить 1000 і більше невідомих. Зараз це здійснюється за допомогою комп’ютерної техніки, в основі якої лежать стандартні методи розв’язання цих систем рівнянь.

В загальному вигляді система рівнянь записується так:

де - невідомих, – рівнянь, 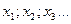- невідомі, 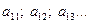- коефіцієнти при невідомих, - вільні члени.

Запишемо таблицю, складену з коефіцієнтів при невідомих

або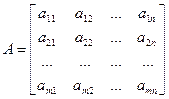

Означення. Прямокутна таблиця, складена з елементів 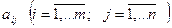деякої множини називається матрицею.

Елементи матриці нумеруються двома індексами: перший і – означає номер рядка, другий 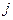- означає номер стовпця. Матриця має розмір (– рядків, - стовпців).

Матриця називається числовою, якщо її елементи 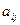- числа, функціональною, якщо її елементи 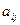- функції, векторною, якщо її елементи 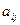- вектори і т.д.

Дві матриці А і В називаються рівними, якщо (відповідні елементи рівні). Рівними можуть бути тільки матриці однакової розмірності.

Матриця, у якої 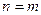називається квадратною:

Якщо m=1, то матриця називається матрицею – рядком:.

Якщо n=1, то матриця називається матрицею – стовпцем:

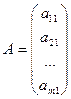
Квадратні матриці, у яких відмінні від нуля тільки елементи головної діагоналі, називаються діагональними:

Якщо всі елементи головної діагоналі діагональної матриці рівні між собою, то така матриця називається скалярною: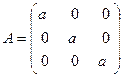

Якщо елементи діагональної матриці дорівнюють одиниці, то така матриця називається одиничною:

Матриця називається трикутною, якщо всі елементи розміщені вище (або нижче) головної діагоналі дорівнюють нулю:

2.2 Дії над матрицями.

1. Додавання матриць.

Означення. Сумою двох матриць А і В називається матриця С, елементи якої

дорівнюють сумі відповідних елементів матриць А і В: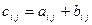

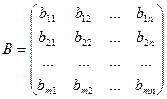
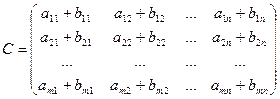
Сума матриць визначена тільки для матриць однакової розмірності.

2. Віднімання матриць.

Означення. Різницею двох матриць А і В називається матриця С, елементи

якої дорівнюють різниці відповідних елементів матриць А і В: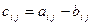

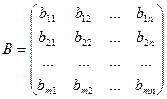
Різниця матриць визначена тільки для матриць однакової розмірності.

3. Множення матриці на число.

Означення. Добутком матриці А на число l називається матриця С, елементи

якої дорівнюють добутку відповідних елементів матриці А на число l: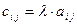

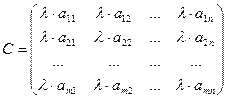
Приклад: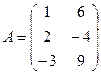

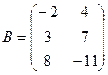
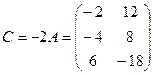
Матриця А називається узгодженою з матрицею В, якщо кількість стовпців матриці А дорівнює кількості рядків матриці В.

Добутком матриць і називається матриця , у якої елемент дорівнює сумі добутків елементів і – того рядка матриці А на відповідні елементи 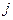- того стовпця матриці В.

, , ,

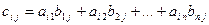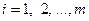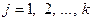
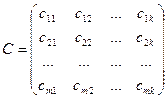
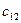- означає, що елементи першого рядка матриці А перемножаються на відповідні елементи другого стовпця матриці В.

Приклад.

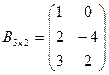
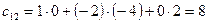
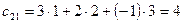
2.3 Обернена матриця.

Квадратна матриця А називається невиродженою, якщо її визначник не дорівнює нулю: 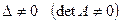. Якщо , то матриця називається виродженою.

Тільки для невироджених матриць вводиться поняття оберненої матриці.

Означення. Нехай А – квадратна матриця. Матриця називається оберненою до матриці А, якщо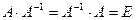

де 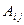- алгебраїчні доповнення елементів визначника матриці А.

Приклад. Знайти матрицю, обернену до матриці А, якщо

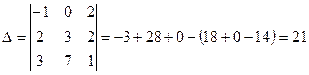
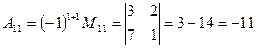
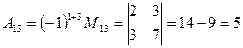
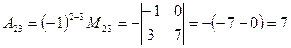
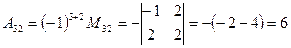
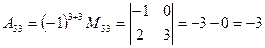
Перевірка: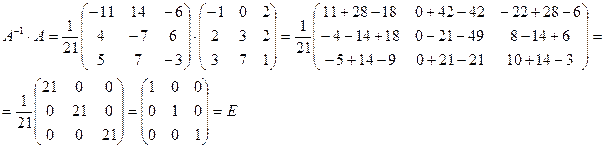

2.4 Методи розв’язування системи лінійних рівнянь.

1. Розв’язування систем лінійних рівнянь за формулами Крамера.

Система трьох лінійних рівнянь з трьома невідомими має вигляд:

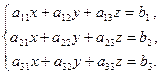
Введемо позначення:

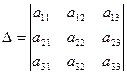
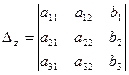
Якщо , то система має єдиний розв’язок і його знаходять за формулами Крамера:

, ,

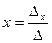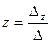
Якщо , а одне з чисел 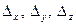не дорівнює нулю, то система не має розв’язку. При 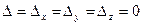система може бути несумісною або мати безліч розв’язків.

Аналогічні формули Крамера справедливі для п лінійних рівнянь з п невідомими.

2. Розв’язування систем лінійних рівнянь методом Гауса.

Метод Гауса – це метод послідовного виключення невідомих. За допомогою

елементарних перетворень, систему приводять до системи вигляду

Таку систему рівнянь називають трикутною (східчастою, трапецієподібною).

Якщо кількість невідомих дорівнює кількості рівнянь, то система має єдиний

розв’язок. Якщо система має рівняння виду ,то вона очевидно несумісна.

3. Матричний метод розв’язування систем лінійних рівнянь

Нехай задано систему п лінійних рівнянь з невідомими

(1)

Введемо матриці , ,

Тоді згідно з правилом множення матриць систему (1) можна записати одним матричним рівнянням з невідомою матрицею Х: .

Якщо матриця А має обернену матрицю , то

Ця формула називається матричним записом розв’язку системи (1). Отже, щоб розв’язати систему рівнянь (1), достатньо знайти матрицю, обернену до матриці системи А, і помножити її на матрицю з вільних членів справа.

Приклад: розв’язати матричним способом систему рівнянь:

Вводимо матриці: , ,

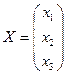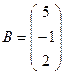
Обчислюємо визначник матриці А:

Знаходимо матрицю , обернену до матриці А: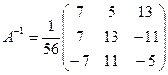

Знаходимо розв’язки за формулою:

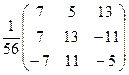
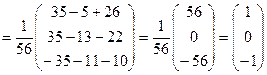
Відповідь: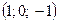

2.5 Ранг матриці.

Нехай маємо матрицю розміром , елементами якої є числа. Вилучаючи з цієї матриці певну кількість рядків і стовпців, можна скласти визначники, які можуть як дорівнювати нулю, так і не дорівнювати нулю. Найбільший порядок таких визначників – це мінімальне з чисел m і n.

Означення. Рангом матриці А () називається найбільший порядок, відмінного від нуля визначника, складеним зазначеним способом з матриці А.

Приклад: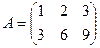

З даної матриці можна скласти три визначники другого порядку і шість визначників першого порядку:

, , , , , , , ,

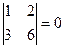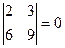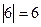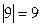
Всі визначники другого порядку дорівнюють нулю, а жоден з визначників першого порядку не дорівнює нулю. Тому .

Ранг матриці не зміниться, якщо:

1) переставити місцями два рядки (стовпці);

2) помножити кожен елемент рядка (стовпця) на один і той самий, відмінний від нуля множник;

3) додати до елементів рядка (стовпця) відповідні елементи іншого рядка (стовпця), помножені на одне і те саме число.

Одним із методів знаходження рангу матриці є метод одиниць та нулів:

~ ~ ~

~ ~ ~ ~

~ ~

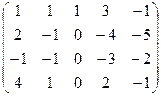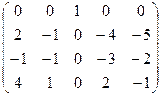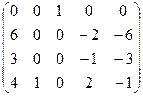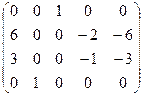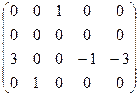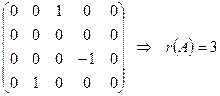
Нехай задано систему m лінійних рівнянь з п невідомими:

Розглянемо основну матрицю А і розширену матрицю даної системи

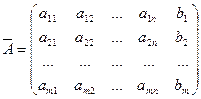
Теорема Кронекера – Капеллі: для того, щоб система лінійних рівнянь була сумісною, необхідно і достатньо, щоб ранг її основної матриці дорівнював рангу розширеної матриці. Якщо 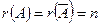, то система має єдиний розв’язок. Якщо 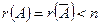, то система має безліч розв’язків.

Приклад: знайти ранг основної і розширеної матриці для системи

~ ~ ~ ~

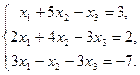
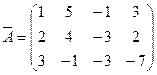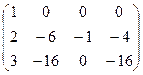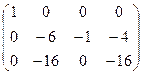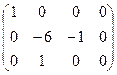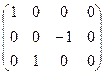~ ~ ~ Þ Þ система має єдиний розв’язок.

2.6 Однорідні системи лінійних рівнянь.

Системи лінійних рівнянь називаються однорідними, якщо праві частини рівнянь дорівнюють нулю.

Однорідна система m лінійних рівнянь з п невідомими має вигляд:

Ця система завжди має нульовий розв’язок: .

Ненульовий розв’язок даної системи (якщо він є) можна знайти методом Гаусса.

Якщо і визначник D системи дорівнює нулю (D=0), то однорідна система має безліч ненульових розв’язків.

Нехай дано систему двох однорідних лінійних рівнянь з трьома невідомими

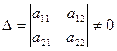
Розв’язок такої системи можна знайти за формулами

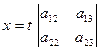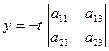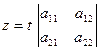, , , де 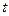- довільне число.

Нехай дано систему трьох однорідних лінійних рівнянь з трьома невідомими

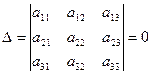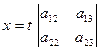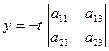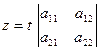Якщо , то система має безліч розв’язків. Нехай у визначнику D існує принаймні один відмінний від нуля мінор другого порядку, наприклад, , тоді розв’язки можна знайти за формулами , , , де 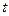- довільне число.

Приклад. Розв’язати систему лінійних однорідних рівнянь

,

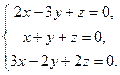
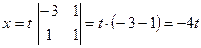
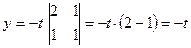
Відповідь:

Контрольні запитання.

4. Що називається матрицею? Назвіть їх види.

5. Які дії можна виконувати над матрицями? Покажіть на прикладах.

6. Як знайти обернену матрицю?

7. Сформулюйте методи розв’язування систем лінійних алгебраїчних рівнянь? Поясніть їх суть.

8. Що називається рангом матриці? Як його знайти?

Яка система рівнянь називається однорідною?

Лекція 3. Векторна алгебра.

Дата добавления: 2014-01-15