Системи координат

План.

1. Системи координат (*).

2. Лінійні операції над векторами (*).

3. Скалярний добуток векторів (*).

4. Векторний добуток векторів (*).

5. Мішаний добуток векторів (**).

6. Базис (*).

7. Ділення відрізка у даному відношенні (*).

Три взаємно перпендикулярні осі Ох, Оу, Оz, які мають спільний початок точку О і однакову масштабну одиницю, утворюють прямокутну декартову систему координат у просторі.

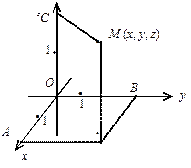
Якщо таких осей дві: Ох і Оу, то маємо систему координат на площині.

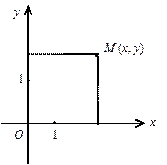
Осі Ох, Оу, Оz називаються відповідно осями абсцис, ординат і аплікат, точка О — початок системи координат. Нехай М — довільна точка в просторі або на площині. Декартовими координатами x, y, z точки М називатимемо відповідно довжини ОА, ОВ, ОС напрямлених відрізків

Таким чином, кожній точці простору відповідає впорядкована трійка чисел (x, y, z), а на площині — впорядкована пара чисел (x, y), тобто встановлюється відповідність між геометричним образом — точкою і впорядкованою множиною чисел

Полярна система координат складається з деякої точки площини О, яка називається полюсом, променя ОА, що виходить з цієї точки і називається полярною віссю. Крім того, задається одиниця масштабу для вимірювання довжин відрізків.

   

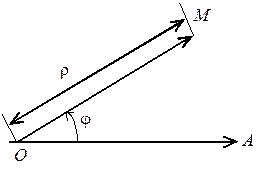
Означення. Полярними координатами точки Мназиваються числа r — відстань від полюса О до точки М і j — кут, на який треба по-
вернути полярну вісь ОА до її збігу з ОМ, проти годинникової стрілки.

Полярний радіус 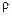може змінюватись у межах < ∞, полярний кут, як правило, змінюється в межах <.

Зв’язок між полярними і декартовими координатами точки встановлюють формули:

Приклад. Знайти полярні координати точки М (2, 2).

З формули (2.1) маємо , tgj = 1. Згідно з останньою рівністю , або 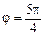, але у = 2 > 0 і х = 2 > 0, маємо . У полярних координатах точка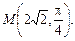

3.2 Лінійні операції над векторами.

3.2.1. Основні поняття.

Скалярні величини характеризуються числовим значенням: маса, час і т.д.

Векторні величини характеризуються числовим значенням і напрямом: швидкість, сила і т.д.

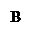
Вектор – це напрямлений відрізок: , точка А – початок вектора, точка В – кінець вектора.

Нульовий вектор – це вектор, у якого початок і кінець співпадають: .

Довжина вектора (модуль, абсолютна величина) - це довжина відрізка, який зображає даний вектор: .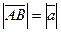

Вектори називаються колінеарними, якщо вони лежать на одній прямій або на паралельних прямих.

Два вектори називаються рівними, якщо вони колінеарні, однаково напрямлені та рівні по довжині.

Проекцією вектора на вісь l називається довжина напрямленого відрізка на осі l.

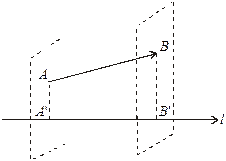
Позначається проекція вектора 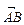на вісь l — пр_l 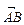. З малюнка випливає формула знаходження проекції вектора на вісь:

пр_l 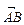= , де 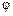— кут між вектором і віссю.

3.2.2. Дії над векторами в геометричній формі.

1) добутком вектора 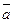на число 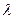називається вектор, модуль якого дорівнює 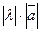, а напрям співпадає з напрямом вектора 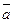, якщо 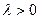і протилежний напряму 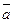, якщо .

2) додавання векторів:

- правило трикутника:

- правило паралелограма: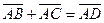

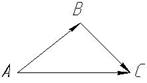
3) віднімання векторів: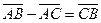

Означення. Координатами вектора називаються його проекції на осі координат.

Дата добавления: 2014-01-15