Правило автоматической остановки имитационного эксперимента

Первый способ. Простейший способ состоит в задании требуемого количества реализаций N. Однако такой подход является грубым из-за того, что на этапе тактического планирования неизвестны распределения выходных переменных.

Второй способ состоит в задании доверительных интервалов для выходных переменных. Остановка прогона машинной модели происходит при достижении заданного доверительного интервала.

Третий способ выполняется путем двухэтапного проведения прогона, когда сначала делается пробный прогон из N₁ реализаций, позволяющий оценить необходимое количество реализаций N. Если N₁> N, то прогон можно закончить, в противном случае необходимо набрать еще (N- N₁) реализаций.

Четвертый способ выполняется путем последовательного анализа для определения минимально необходимого количества реализаций N, которое рассматривается при этом как случайная величина, зависящая от N-1 предыдущих реализаций.

Пример. Построение линейной регрессионной модели (теоретически данный вопрос рассматривался в п.п. 4.5).

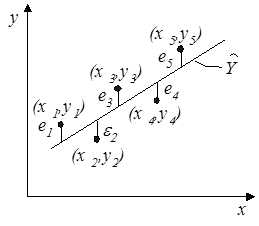
Рис. 4.16. График эксперимента

На рис. 4.16 показаны точки (x_i,y_i), 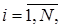полученные в машинном эксперименте с моделью системы. Делаем предположение, что модель результатов машинного эксперимента графически может быть представлена в виде прямой линии 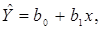где 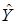– величина, предсказываемая регрессионной моделью. Требуется получить такое значение коэффициентов 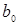и 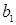, при которых сумма квадратов ошибок является минимальной.

На рис. 4.16 ошибка для каждой экспериментальной точки определяется как расстояние по вертикали от этой точки до линии регрессии .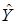

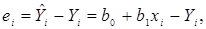
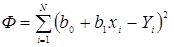– сумма квадратов ошибок,

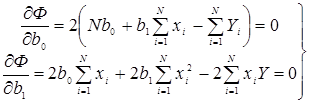
Решая систему нормальных уравнений получим

,

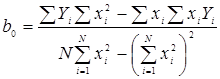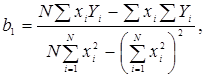
N – число реализаций при моделировании системы.

Мерой ошибки регрессионной модели служит среднеквадратическое отклонение

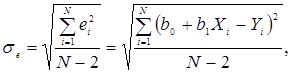
Для нормального распределенных процессов приблизительно 67% точек находится в пределах одного отклонения 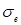от линии регрессии – труба А, и 95% точек – в пределах 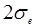– труба В (рис. 4.17).

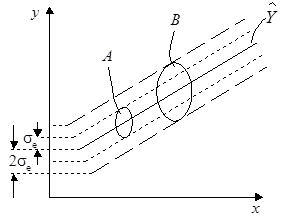Рис. 4.17. Пределы отклонения экспериментальных точек

Для проверки точности оценок 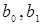и адекватности модели используются критерии Стьюдента и Фишера.

Дата добавления: 2014-01-15