Понятие о матрице перемещений

Определение перемещений в матричной форме

Лекция тринадцатая

13.1. Понятие о матрице перемещений

13.2. Вычисление интегралов формулы Мора в матричной форме в случае произвольных подынтегральных функций

13.3. Вычисление интегралов формулы Мора в матричной форме в случае линейных подынтегральных функций Ф_ik(s), Ф_Fk(s)

13.4. Определение перемещений от силового воздействия

13.5. Определение перемещений от температурных воздействий

13.6. Определение перемещений от кинематических воздействий

13.7. Определение перемещений от воздействий различного характера

13.8. Вопросы для самопроверки

13.9. Рекомендуемая литература

В инженерных расчётах часто возникает необходимость определения группы различных перемещений узлов и сечений заданного сооружения от независимых друг от друга внешних воздействий – силовых, температурных, кинематических. Таблица величин этих перемещений, составленная по определенным правилам, называется матрицей перемещений.

Например, в раме, показанной на рис. 13.1, требуется определить горизонтальное перемещение узла А, вертикальное перемещение сечения "к" и угол поворота сечения "а" отдельно от равномерно распределенной нагрузки q, сосредоточенной силы F, сосредоточенного момента М, изменения температуры и смещения опорных связей D₍₁₎, D₍₂₎. Установим следующий порядок формирования матрицы перемещений. В её первой строке будем фиксировать только величины горизон­тального переме­ще­ния узла А, во второй – вертикального пере­ме­ще­ния сечения "к", в третьей – угла пово­рота сечения "а". По­рядок записи величин искомых перемещений в каждой строке зависит от принятой нумерации внешних воздействий. Для нашего примера примем: первое воздействие – равномерно распределённая нагрузка q, второе – сосредоточенная сила F, третье – сосредоточенный момент М, четвёртое – изменение температуры , пятое – смещение опорных связей D₍₁₎, D₍₂₎. С учётом установленных правил получим матрицу перемещений

D = .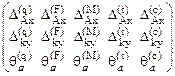

В общем случае для любой задачи число строк матрицы перемещений равно числу определяемых перемещений различного характера, а число столбцов – числу независимых внешних воздействий (собственный вес конструкций, снег, ветер, технологическая нагрузка, изменение температуры, смещение опорных связей и т.д.). В первом столбце матрицы перемещений принято записывать группу искомых перемещений от постоянной нагрузки.

В настоящей лекции рассматривается вычисление элементов матриц перемещений в матричной форме. Для успешного усвоения материала этой и последующих лекций читателям полезно повторить некоторые разделы линейной алгебры, связанные с действиями транспонирования, сложения, вычитания, умножения и обращения матриц.

Дата добавления: 2014-01-15