Для описания квантовых систем вводится фазовое пространство импульсов и координат

Фазовое пространство. Фазовый объем и фазовая ячейка. Плотность энергетических состояний.

Энергия Ферми. Расчет энергии Ферми при абсолютном нуле для металлов.

Фазовое пространство. Фазовый объем и фазовая ячейка. Плотность энергетических состояний.

Лекция 16

ОСНОВЫ КВАНТОВОЙ СТАТИСТИКИ

Липоевая кислота:сахарный диабет, атеросклероз.

Биотин: дерматиты, ломкость ногтей, анемии, депрессия.

Вит РР: пеллагра: эритема, дистрофия нервной системы и ЖКТ.

Вит С: цинга: геморрагии, утомляемость, дистрофии, гиперкератоз.

2. Распределение Бо­зе-Эйнштейна и Ферми − Дирака.

4. Средняя энергия электрона и давление электронного газа в ме­таллах.

Квантовой статистикой называется теория сис­тем, состоящих из большого числа частиц, под­чиняющихся квантовым закономерностям.

При этом на возможные состояния системы накладывает­ся ограничение:

каждому квантовому состоянию системы с i степенями свободы (число степеней свободы - число независимых координат, описывающих систему) соответствует ячейка (клетка) в ее фазовом пространстве, имеющая объем h³.

Это соответ­ствует соотношению неопределенности Гейзенберга:

Т.е.минимальный объем фазового пространства равен h³.

Изменение состояния системы может происходить лишь дискретно; система из одних клеток фазового объ­ема переходит «скачком» в другие. В квазиклассическом приближении переход в соседнюю квантовую ячейку соот­ветствует очень малому изменению свойств системы. Можно считать, что свойства системы изменяются непрерывно.

Распределение частиц по ячейкам 6-мерного фазо­вого пространства (х,y_y,z, р_х, р_у, p_z) характеризует определенное микросостояние системы.

Задачей квантовой статистики является отыскание функции распределения системы частиц в фазовом прост­ранстве. В основе квантовой статистики лежит прин­цип неразличимости тождественных частиц.

В кван­товой статистике при решении задачи о распределении частиц в фазовом пространстве не имеет смысла поста­новка вопроса о том, какая из частиц находится в данной ячейке (клетке) фазового пространства - надо найти число частиц, находящихся в данной ячейке.

Микросо­стояние системы не изменяется от перестановки частиц как внутри данной клетки фазового пространства, так и между клетками.

2. Распределение Бо­зе-Эйнштейна и Ферми − Дирака.

Статистике Бо­зе-Эйнштейна подчиняются системы частиц с целым спином - бозоны (например, фотоны и некоторые ядра); для этих частиц нет ограничения на их количество, которое может находиться в данной клетке 6-мерного фазового пространства, т. е. в данном квантовом состоянии.

Обычно определяют среднюю «заселенность» состояний с данной энергией, т. е. среднее число частиц n_i в одном состоянии, которое называется функцией распределения Бозе - Эйнштейна:

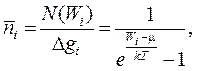(16-1)

гдс μ - химический потенциал, отнесенный к одной частице,

k - постоянная Больцмана,

ΔN(W_i)- полное число частиц с энергией W_i,,

Δg_i - число состояний.

Индекс i иногда опускается, так как эта функция распределения справедлива для любого из элементов фазового объема.

Частицы, имеющие полуцелый спин подчиняются рас­пределению Ферми - Дирака.Этой статистикой описывается поведение систем фермионов(электронов, протонов, нейтронов и др.) - ча­стиц, подчиняющихся принципу запрета Паули. В таких системах частиц в одном квантовом состоянии может находиться не более одной частицы. Функция распределения Ферми — Дирака :

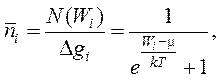(16-2)

Функции распределения в классической и кванто­вых статистиках могут быть записаны в единой формуле:

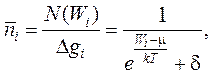(16-3)

Для распределения Максвелла - Больцмана δ =0; для распределения Бозе - Эйнштейна δ = - 1;для распреде­ления Ферми - Дирака δ= + 1

На рис. 16-1 показаны эти три функции распределения.

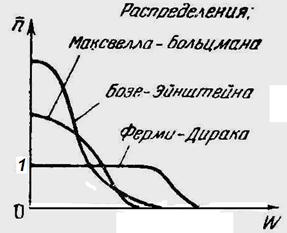
Рис. 16-1

Дата добавления: 2014-01-15