Физики и биомедицинской техники

Откуда

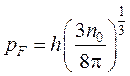(16-5)

где n₀=N/V - число электронов в единице объема. Согласно (16-5) наибольшая энергия электрона при Т = 0 равна

(16-6)

Или:

При плотности свободных электронов в металлах n₀ ~10²⁸ м^-3энергии Ферми соответствует темпе­ратура Т классического газа, равная

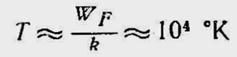
4. Средняя энергия электрона при абсолютном нуле температуры, давление и теплоемкость электронного газа в ме­таллах.

При высоких температурах энергия молекулы газа может меняться непрерывно, т.е. не квантуется. Однако, при низких температурах энергия теплового движения молекулы становится сравнимой с энергией движения электронов в оболочках атомов и начинает принимать дискретные значения.

А). Понятие вырождения газов

Вырождением идеальных газовназывается откло­нение их свойств от свойств обычных газов, вызванное квантовыми свойствами частиц. Вырождение га­зов становится существенным при низких температурах и больших плотностях.

При ехр(-W_F /kT) >> 1 функции распределения Бозе— Эйнштейна и Ферми—Дирака пе­реходят в классическую функцию распределения Максвкелла-Больцмана, N=N₀ ехр(-W_F /kT). При этом выполняется условие

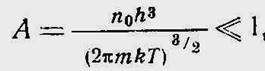(16-7)

где п₀ - число молекул в ед. объемагаза, т - масса молеку­лы, Т- абсолютная температура, k - постоянная Больцмана, h - постоянная Планка. Величина А называется параметром вырождения.

При А~1 система подчиняется квантовой статистике, т.е. проявляются ее квантовые свойства. Температура, при которой сказываются квантовые свойства, называется температурой вырождения. Температурный критерий вырождения для газов ( Т₀ -температура вырождения):

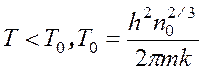(16-8)

При Т >>T₀ газ не вырожден и подчиняется классичес­кой статистике.

Пример 1:. Для водорода при нормальных условиях (Т = 300° К и n=310²⁵ м^-3 ) параметр А~10^-5<< 1. Это соответ­ствует температуре вырождения Т₀ ≈ 1° К. Т.е. водород при температуре ниже T₀~1K является вырожденным

Для газов более тяжелых, чем водород, параметр А еще мень­ше, и следовательно, газы при нормальных давлениях и температурах никогда не бывают вырождены.

Вырож­дение, вызванное квантовыми свойствами газов, сказыва­ется значительно меньше, чем отклонения газов от иде­альности, связанные с ван-дер-ваальсовыми силами вза­имодействии между молекулами.

Уравнение состояния идеального газа Бозе-Эйнштейна:

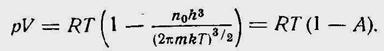
Пример 2: Для электронов в металлах п~ 10²⁸ м^-3 Т₀ ~2 10⁴ °К. Следовательно, электрон­ный газ в металлах всегда вырожден (вследствие малой массы электрона и большой плотно­сти частиц), т.е. подчиняется квантовому распределению.

Пример 3: Газ протонов с массой частицы m=2*10^{-27 к г} при плотностях

n ~10²⁸ м^-3величина Т₀ ≈ 1° К.

Пример 4: Фотонный газ всегда вырожден, так как для него Т₀=∞ (масса покоя фотона m₀=0).

Б). Вычисление средней энергии электронов при абсолютном нуле температуры.

Если энергией W₁ обладает ΔN₁ электронов, энергией W₂ - ΔN₁ электронов и т.д., то полная энергия электронов в объеме V:

(16-9)

Согласно принципу Паули число электронов при температуре Т=0 равно числу состояний. Поэтому, dN можно выразить через энергию, определив число состояний в фазовом пространстве (см. рис.16-5):

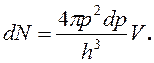(16-10)

Используя соотношение между энергией электрона и его импульсом, перепишем (16-10):

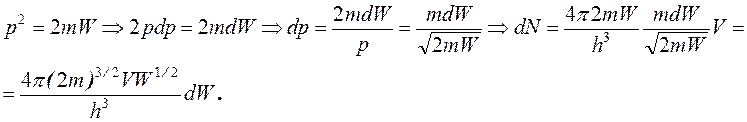
(16-11)

Учитывая, что при N=N₀ W=W_F, подставим (16-11) в (16-9) и проинтегрируем полученное соотношение в пределах от 0 до W_F:

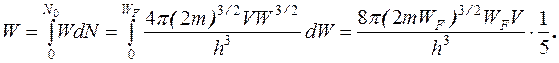(16-12)

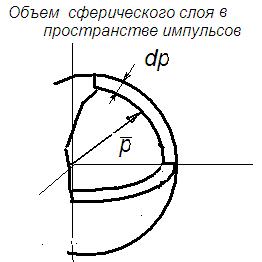
Рис.16-5

Далее, выразим из (16-6), концентрацию n₀:

(16-13)

Подставим (16-13) в (16-12) и получим выражение для полной энергии W, откуда получим среднюю энергию:

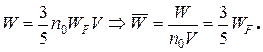(16-14)

Или

Давление электронного газа в металле при Т→ 0 (используем основное уравнение МКТ):

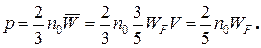
составляет десятки тысяч атмосфер.

Можно показать, что W_F зависит от температуры. С учетом этой зависимости

внутренняя энергия U электронного газа равна:

(16-15)

Где N - общее число электронов в объеме V.

Молярная теплоемкость C_aV электронного газа (дифференцируем (16-15):

Сравнение с классическим выражением для теплоем­кости C_aV одноатомного газа дает:

так как 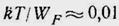при всех температурах, когда электронный газ еще вырожден. Теплоемкость электрон­ного газа в металлах ничтожно мала. Это связано с тем, что в процессе изменения внутренней энергии при на­гревании участвует незначительное число электронов, находящихся в состояниях, соответствующих «области спада» функции распределения Ферми - Дирака при Т≠0.

«Утверждаю» Заведующий кафедрой _________________ С.И. Шарапов «____»___________ 2010 г.

Дата добавления: 2014-01-15