Приклад. Розв’язати рівняння

Теорема 2. Якщо умова (4) не виконується і всі корені рівняння (1) різні, то рівняння (1) можна перетворити в рівняння виду (2). Якщо умова (4) виконується, то рівняння (1) мож­на перетворити в рівняння виду (3).

Доведення. Для відшукання коефіцієнтів рівняння (2) маємо систему рівнянь

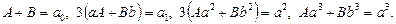(6)

Із перших двох рівнянь (6) при 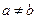знаходимо:

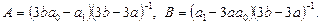(7)

Підставивши А та В в останні два рівняння (6) і поділивши ці рівняння на 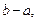дістанемо симетричну систему рівнянь для a, b

яку можна записати у вигляді

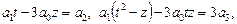(8)

де

Ця система рівнянь має розв’язок

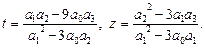(9)

Коефіцієнти a, b є коренями квадратного рівняння

Дискримінант D цього рівняння

лише ненульовим дільником 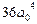відрізняється від дискримінан­та зведеного кубічного рівняння (1).

Якщо корені рівняння різні, то 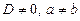і з рівнянь (7) знаходимо A, B. Для рівняння (1) з дійсними коефіцієнтами всі коефіцієнти рівняння (2) будуть дійсними при

Зауважимо, що з рівнянь

можна знайти значення 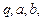виражені через корені 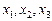рів­няння (1):

Рівняння 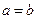зводиться до рівнянь 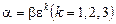і рівносильне одній із рівностей

Якщо виконується умова (4), то рівняння (1) можна записати у вигляді рівняння (3). Для відшукання коефіцієнтів рівняння (3) маємо систему рівнянь

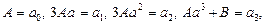
розв’язну в разі виконання умови (4). Рівняння (1) можна записати у вигляді

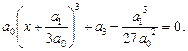
Приклад 1. Розв’язати кубічне рівняння

Ø Згідно з формулами (7)—(9) знаходимо:

Рівняння виду (2) набирає вигляду

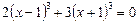
і має розв’язок

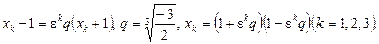
Рівняння має дійсний корінь

Приклад 2. Розв’язати рівняння

.

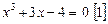Ø Знаходимо значення

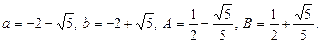
Рівняння виду (2) набирає вигляду

і має розв’язок 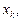який визначається з рівнянь

При 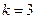знаходимо дійсний корінь

4.13. Метод Феррарі для розв’язування рівнянь
четвертого степеня

Метод Феррарі зводить розв’язування рівняння четвертого степеня до розв’язування кубічного рівняння відносно введеного параметра. Визначивши параметр, знаходять невідоме.

Приклад. Розв’язати рівняння

.

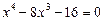Ø Виділимо повний квадрат у лівій частині рівняння, подавши його у вигляді

.

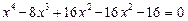Дістанемо таке рівняння:

.

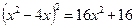Увівши параметр 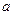, виділяємо повний квадрат:

.

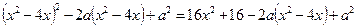
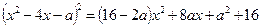Виберемо параметр 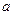так, щоб права частина була повним квадратом. Для цього дискримінант квадратного тричлена має дорівнювати нулю:

.

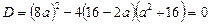Для параметра 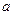дістали кубічне рівняння

.

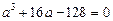З’ясувавши, що 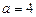— корінь цього рівняння, дістанемо рів­няння відносно :

,

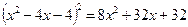або

.

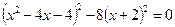Розглядаючи цей вираз як різницю квадратів двох виразів, подамо її у вигляді

.

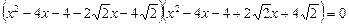Рівняння розпадається на два рівняння

;

.

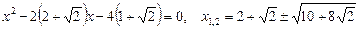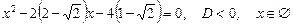Приклад. Розв’язати рівняння четвертого степеня

.

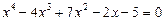Ø Виділимо повний квадрат:

,

,

. (*)

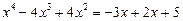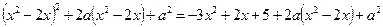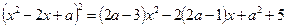Тричлен у правій частині буде повним квадратом, якщо його дискримінант дорівнює нулю:

.

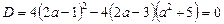Дістанемо кубічне рівняння відносно а:

.

Добором знаходимо корінь 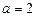цього кубічного рівняння.

Підставивши в рівняння (*) значення 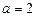, дістанемо рівняння відносно х:

,

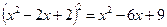або

,

,

.

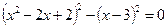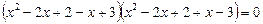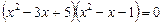Остаточно знаходимо розв’язки

,

.

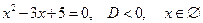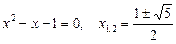4.14. Метод заміни рівняння
системою двох рівнянь

Іноді розв’язування рівняння можна спростити, звівши його до системи рівнянь із двома невідомими.

Приклад. Розв’язати рівняння

.

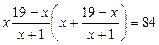Ø Узявши 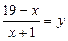, дістаємо систему рівнянь

Нехай 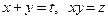. Тоді дістанемо систему рівнянь:

,

.

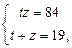
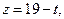
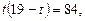
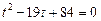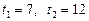Знаходимо із систем рівнянь:

1)

2)

Приклад. Розв’язати рівняння

.

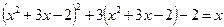Ø Позначивши 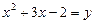, дістаємо систему рівнянь

Віднімаючи почленно перше рівняння від другого маємо:

;

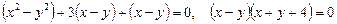1)

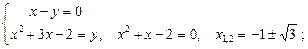
2)

4.15. Розв’язування рівнянь
у цілих числах

Розглянемо спочатку найпростіше рівняння

. (1)

Воно має чотири розв’язки в цілих числах

.

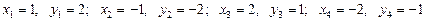До рівняння виду (1) зводяться складніші рівняння та системи рівнянь.

Приклад. Розв’язати систему рівнянь у цілих числах:

Ø За аналогією до рівняння (1) розв’язуємо такі системи:

1)

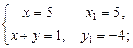
2)

3)

4)

Приклад. Розв’язати в цілих числах рівняння

.

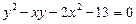Ø Дане рівняння можна записати у вигляді

,

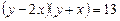тобто звести до рівняння виду (1):

1)

2)

3)

4)

Розглянемо складніший приклад.

Приклад. Розв’язати в цілих числах рівняння

.

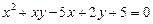Ø Уведемо параметр :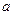

.

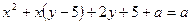Знаходимо дискримінант лівої частини рівняння:

.

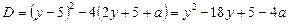Корінь з дискримінанта добувається, якщо .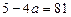

При цьому знаходимо корені рівняння

,

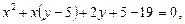
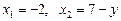а також розклад лівої частини на множники:

.

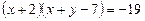Перетворюємо вихідне рівняння до виду (1):

1)

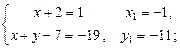
2)

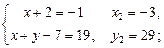
3)

4) .

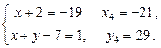1. Формули для розв’язків квадратного рівняння.

2. Умова знакосталості квадратного тричлена.

3. Формули Вієта.

4. Які рівняння зводяться заміною до квадратного?

5. Метод Феррарі.

6. Розв’язування рівнянь у цілих числах.

Розв’язати рівняння (1 — 45). Відповідь

1. .

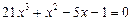2. .

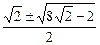
3. .

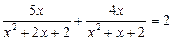4. .

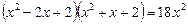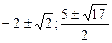
5. .

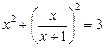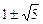
6. .

7. .

8. .

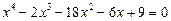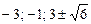
9. .

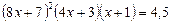10. .

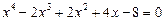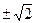
11. .

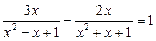12. .

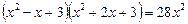13. .

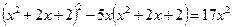14. .

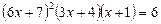15. .

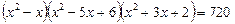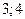
16. .

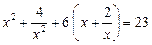17. .

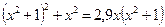18. .

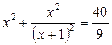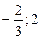
19. .

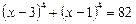20. .

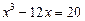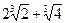
21. .

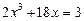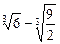
22. .

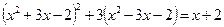23. .

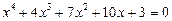24. .

25. .

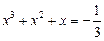26. .

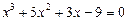27. .

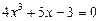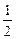
28. .

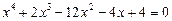29. .

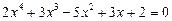30. .

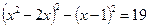31. .

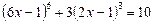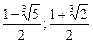
32. .

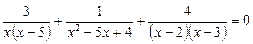33. .

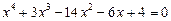34. .

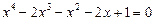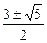
35. .

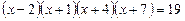36. .

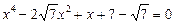37. .

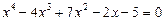38. .

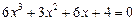39. .

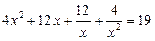40. .

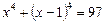41. .

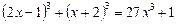42. .

43. .

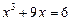44. .

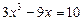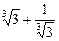
45. . .

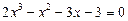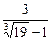ЛЕКЦІЯ

ІРРАЦІОНАЛЬНІ
РІВНЯННЯ

Ірраціональним називають таке рівняння, ліва і права частини якого є алгебраїчними виразами, хоча б один із яких ірраціональний.

Нагадаємо, що ірраціональними називають такі алгебраїчні вирази, які крім дій додавання, віднімання, множення, ділення та піднесення до степеня з натуральним показником містять також і дії добування кореня m-го степеня.

Ірраціональні вирази виду 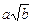називають також радикалами.

Приклади ірраціональних рівнянь:

; ; .

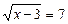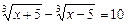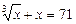В елементарній алгебрі розглядаються лише такі ірраціональні рівняння, в яких радикали парного степеня припускаються арифметичними (невід’ємними), а непарного степеня — додатними або від’ємними, залежно від знака підкореневого виразу.

Загальний метод розв’язування ірраціонального рівняння полягає в тому, що спочатку ізолюють один радикал, а далі обидві частини рівняння підносять до степеня, потім знову ізолюють радикал і т. д. Будь-яке ірраціональне рівняння піс­ля скінченної кількості таких перетворень можна звести до раціонального.

Рівняння, яке дістаємо в результаті, узагалі кажучи, не еквівалентне заданому. Тому, знайшовши розв’язки цього рівняння, потрібно перевірити їх підставленням у дане рівняння і відкинути як сторонні ті з них, які не є розв’язками. Проте якщо обидві ча­стини ірраціонального рівняння підносились до непарного степеня, то перевіряти розв’язок не обов’язково, бо в цьому разі прийдемо до рівняння, еквівалентного даному.

Якщо рівняння містить радикали з невідомим у знаменнику, то його потрібно звільнити від знаменника, виконавши відповідні перетворення.

Перш ніж приступити до розв’язування ірраціонального рівняння, доцільно визначити область допустимих значень (ОДЗ) для невідомого. У деяких випадках після цього відпадає потреба в розв’язанні.

Нехай, скажімо, маємо рівняння

.

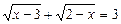Для першого радикала ОДЗ становлять значення 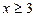, а для другого 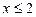. Отже, у множині дійсних чисел це рівняння не має розв’язків (не існує дійсних значень х, для яких обидва підкореневі вирази невід’ємні).

5.1. Розв’язування найпростіших ірраціональних рівнянь
із відшуканням ОДЗ

Приклад. Розв’язати ірраціональне рівняння

Ø Добуток двох множників дорівнює нулю тоді й тільки тоді, коли принаймні один із них дорівнює нулю. Отже, маємо: .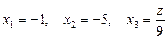

Значення 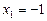, 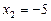не входять в ОДЗ 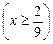рівняння і не є його коренями.

Приклад. Розв’язати рівняння

.

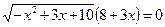Ø Знаходимо корені рівнянь 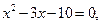і 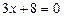: 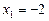, , 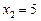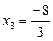. Корінь 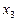сторонній, оскільки він не входить в ОДЗ .

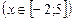Приклад. Розв’язати рівняння

.

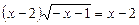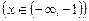Ø Рівняння має очевидний корінь , що не входить в ОДЗ і є стороннім. Поділивши обидві частини рівняння на х – 2, дістанемо:

, , . ×

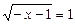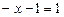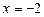Зауважимо, що іноді перш ніж розв’язувати рівняння, доцільно з’ясувати, чи можуть його ліва та права частини бути рівними між собою. Якщо ні, то рівняння, очевидно, не має розв’язків.

Приклад. Розв’язати рівняння

.

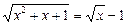Ø Знайшовши ОДЗ 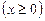, доходимо висновку, що там виконується нерівність 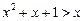, звідки .

Тому дане рівняння не має розв’язків.

Приклад. Розв’язати рівняння

.

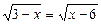Ø Знаходимо ОДЗ із нерівностей:

Звідси випливає, що .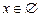

Рівняння розв’язків не має.

Приклад. Розв’язати рівняння

.

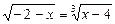Ø Знаходимо ОДЗ: 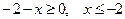. В ОДЗ права частина рівняння від’ємна, а ліва частина невід’ємна. Рівняння не має розв’язків, .

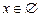5.2. Піднесення обох частин рівняння до квадрата

Приклад. Розв’язати рівняння

.

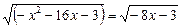Ø Підносимо обидві частини рівняння до квадрата:

звідки.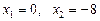

Значення 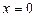не є коренем рівняння, оскільки при х = 0 обидва підкореневі вирази від’ємні.

Приклад. Розв’язати рівняння

.

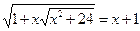Ø Підносимо обидві частини рівняння до квадрата:

звідки відразу знаходимо 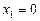, а далі після відповідних перетворень маємо:

.

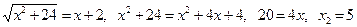Приклад. Розв’язати рівняння

.

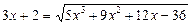Ø Підносимо обидві частини рівняння до квадрата:

.

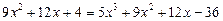Після зведення подібних членів дістаємо:

.

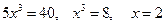Приклад. Розв’язати рівняння

.

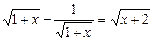Ø Виконаємо перетворення:

.

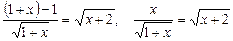Піднісши обидві частини останнього рівняння до квадрата, дістанемо:

.

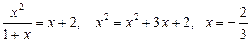Знайдене значення х не задовольняє рівняння, а отже, .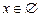

Приклад. Розв’язати рівняння

.

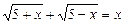Ø Підносимо обидві частини рівняння до квадрата:

,

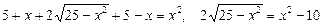а далі знову підносимо обидві частини перетвореного рівняння до квадрата:

.

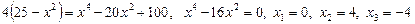Значення 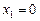, 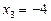не задовольняють дане рівняння.

Приклад. Розв’язати рівняння

.

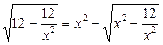Ø Підносимо обидві частини рівняння до квадрата:

.

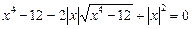Після перетворень дістаємо:

.

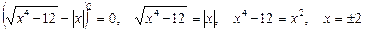5.3. Метод заміни

Нерідко заміною підкореневого виразу можна звести ірраціональне рівняння до раціонального.

Приклад. Розв’язати рівняння

.

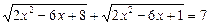Ø Позначивши 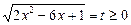, дістанемо рівняння

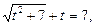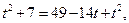або звідки .

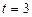Повертаючись до початкових позначень, маємо:

.

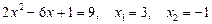Приклад. Розв’язати рівняння

.

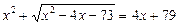Ø Позначивши 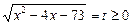, дістанемо рівняння

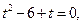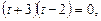або звідки .

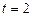Повертаючись до початкових позначень, маємо:

.

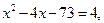
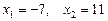Приклад. Розв’язати рівняння

.

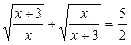Ø Позначивши 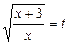, дістанемо рівняння

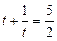, звідки .

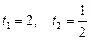Повертаючись до початкових позначень, маємо:

;

.

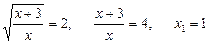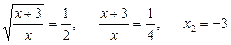Приклад. Розв’язати рівняння

.

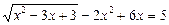Ø Позначивши 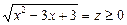, дістанемо рівняння

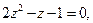звідки .

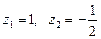Повертаючись до початкових позначень, маємо:

.

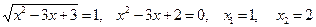Приклад. Розв’язати рівняння

.

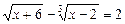Ø Позначимо 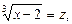тоді .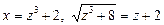

Розв’язуючи рівняння: 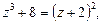дістаємо: .

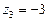Остаточно маємо: .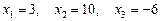

Приклад. Розв’язати рівняння

.

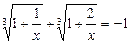Ø Позначивши 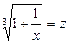, дістанемо рівняння

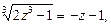або 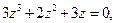звідки .

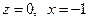Приклад. Розв’язати рівняння

.

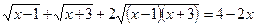Ø Виконаємо таке перетворення:

,

.

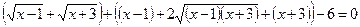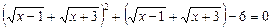Скориставшись заміною 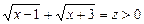, дістанемо:

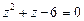, звідки .

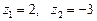Повертаємось до початкових позначень:

,

.

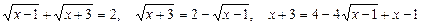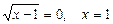Приклад. Розв’язати рівняння

.

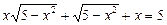Ø Позначимо 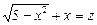. Тоді дане рівняння набере вигляду

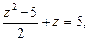звідки .

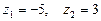Рівняння 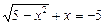розв’язків не має.

Розв’язуючи рівняння 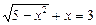, дістаємо: .

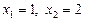Приклад. Розв’язати рівняння

.

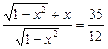Ø Позначивши 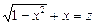, дістанемо рівняння

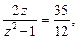звідки .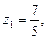

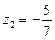Повертаючись до початкових позначень, маємо:

Корінь 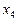— сторонній.

Приклад. Розв’язати рівняння

.

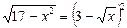Ø Позначивши 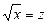, дістанемо рівняння

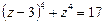, звідки .

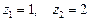Повернувшись до початкових позначень, знайдемо .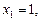

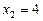5.4. Виділення повного квадрата

Розв’язуючи ірраціональні рівняння, часто використовують метод виділення повного квадрата.

Приклад. Розв’язати рівняння

.

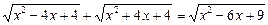Ø Виділимо під радикалами повний квадрат

,

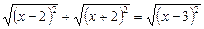або

.

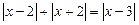Розв’язуючи це рівняння на проміжках 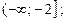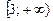, знаходимо корені , .

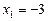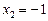Приклад. Розв’язати рівняння

.

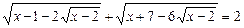Ø Позначивши 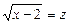, дістанемо рівняння

.

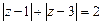Звідси випливає: .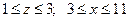

Приклад. Розв’язати рівняння

.

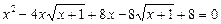Ø Перетворимо ліву частину рівняння:

,

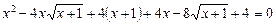або .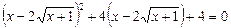

Далі маємо:

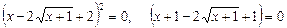
або 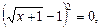звідки .

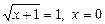Приклад. Розв’язати рівняння

.

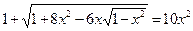Ø Під знаком кореня маємо повний квадрат:

,

.

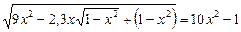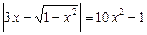Знаходимо ОДЗ:

З першої системи визначаємо 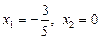. Корінь 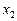— сторонній.

З другої системи маємо .

Корінь 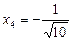— сторонній.

Приклад. Розв’язати рівняння

.

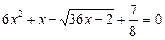Ø Виділяємо повний квадрат:

.

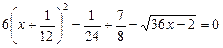У результаті заміни 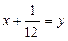дістаємо рівняння

.

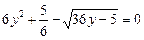Позначивши , запишемо систему:

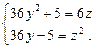
Узявши 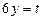, дістанемо систему

Віднімаючи почленно друге рівняння від першого, маємо:

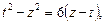звідки .

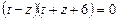Розв’язуємо останнє рівняння:

.

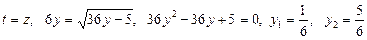Оскільки 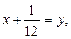то .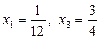

5.5. Множення обох частин рівняння на вираз,
спряжений до виразу в лівій частині

Приклад. Розв’язати рівняння

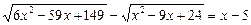. (1)

Ø Помножимо обидві частини рівняння на вираз, спряжений до виразу в лівій частині:

.

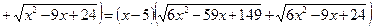Після перетворень дістаємо рівняння

,

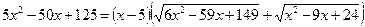або

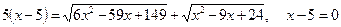. (2)

Маємо корінь рівняння 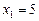. З рівнянь (1), (2) випливає:

.

Підносимо обидві частини цього рівняння до квадрата:

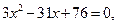звідки .

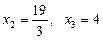Корінь 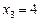не задовольняє рівняння.

Приклад. Розв’язати рівняння

.

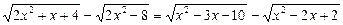Ø Ліву і праву частини рівняння помножимо і поділимо на відповідні спряжені вирази:

.

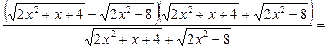
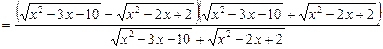Виконавши перетворення, дістенемо рівняння

,

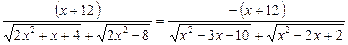ліва і права частини якого мають спільний множник .

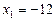Приклад. Розв’язати рівняння

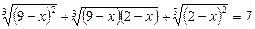
з кубічними ірраціональностями.

Ø Помноживши ліву і праву частини даного рівняння на вираз 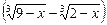, спряжений до суми першого та третього до-
данків.

Дістанемо різницю кубів:

.

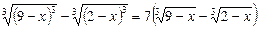Звідси після спрощень маємо:

.

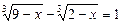Виконавши заміну 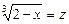, , 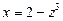дістанемо:

, , ; , .

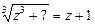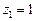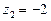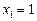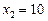5.6. Однорідні ірраціональні рівняння

Рівняння виду

називається однорідним. Воно зводиться до квадратного рівняння заміною

.

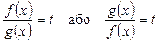Приклад. Розв’язати рівняння

.

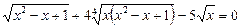Ø Скориставшись позначенням

,

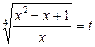дістанемо рівняння

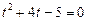, звідки , .

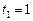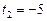Переходячи до початкових позначень, маємо:

, .

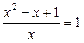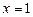Приклад. Розв’язати рівняння

.

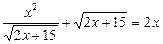Поділивши обидві частини рівняння на х, дістанемо:

.

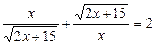Візьмемо 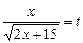, тоді 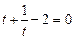, звідки .

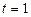У початкових позначеннях маємо:

, , , .

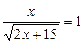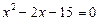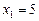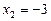Корінь 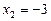не задовольняє рівняння.

5.7. Розклад на множники

.

Ø Знайдемо спочатку ОДЗ з нерівностей

, , ;

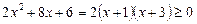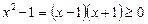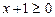ОДЗ: ; .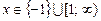

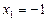Винесемо спільний множник за дужки:

.

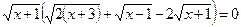Піднесемо обидві частини рівняння до квадрата і виконаємо відповідні перетворення:

;

.

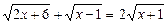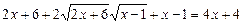Остаточно маємо: , .

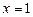Дата добавления: 2014-01-11