Неоднородная система линейных уравнений

Пример

Теорема 8.2. Для того чтобы однородная система n линейных уравнений с n неизвестными обладала нену­левыми решениями, необходимо и достаточно, чтобы ее определитель D был равен нулю.

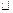Условие D = 0 здесь необходимо, так как если D 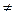0, то система имеет единственное и, значит, только нулевое решение. Это условие также и достаточн о, так как если D = 0, то ранг матрицы коэффициентов системы r < n, и система имеет бесчисленное множество (ненулевых) решений.

Пусть

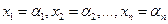
— какое-нибудь ненулевое решение однородной систе­мы (8.1). Это решение можно рассматривать как строк у 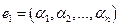, состоящую из п элементов. Тогда строка

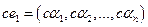
тоже, очевидно, будет решением системы (8.1). Далее, если

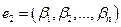
— какое-то другое решение системы (8.1), то при любых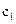и 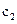линейная комбинация

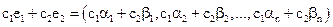
этих решений тоже будет решением системы, так как если

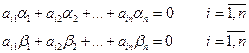= 0,

то и

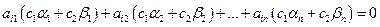
Вывод, любая линейная комбинация решений однородной системы (8.1) тоже будет ее решением.

Найдем такие линейно независимые решения системы (8.1), через которые линейно выражались бы все осталь­ные ее решения.

Линейно независимая система решений 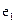, е₂,..., е_к уравнений (8.1) называется фундаментальной если каждое решение системы (8.1) является линейной комбинацией решений , е₂,..., е_к.

Теорема 8.3 (о существований фундаментальных систем решений). Если ранг r матрицы коэффициентов системы уравнений (8.1) меньше п, то эта система обладает фундаментальными системами решений.

§ Пусть ранг r матрицы А ко­эффициентов системы (8.1) меньше п, и пусть, для опре­деленности, минор D r-го порядка, стоящий в левом верхнем углу матрицы А, отличен от нуля:

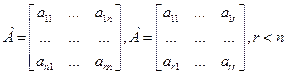
Перенеся свободные неизвестные 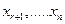первых r уравнений системы (8.1)в правые части, получим си­стему

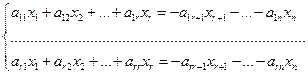
Придавая свободным неизвестным значения ,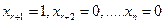

получим соответствующие значения 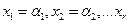, первых r неизвестных. Это дает нам стро­ку — решение системы (8.1)

.

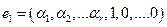Аналогично, придавая свободным неизвестным значения

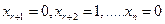
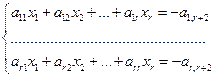
и вычисляя соответствующие значения неизвестных, получим строку

,

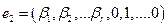и т. д.

Так мы найдем всего k = п — r решений систе­мы (8.1):

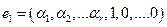
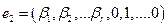
………………………. (8,2)

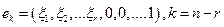
Эти k строк между собой линейно независимы, ибо ранг образованной ими матрицы

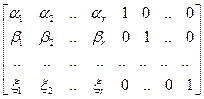
в точности равен k. (В этой матрице есть отличный от нуля минор k -гопорядка, например, содержащий по­следние k столбцов.)

Покажем теперь, что решения 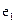, е₂,..., е_к (8.2) дей­ствительно образуют фундаментальную систему. Для этого остается показать, что каждое решение систе­мы (8.1) линейно выражается через 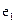, е₂,..., е_к.

■ Пусть

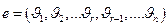
— произвольное решение системы (8.1). Рассмотрим строку

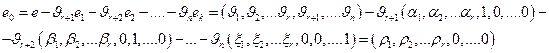
Легко видеть, что все элементы, состоящие на послед­них k местах этой строки, равны нулю, т. е. что

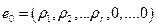
Будучи линейной комбинацией решений, строка е₀ сама будет решением системы (8.1). А так как значения всех свободных неизвестных в е₀ равны нулю, то из од­нородной в этом случае системы (23), определитель которой отличен от нуля, получаем, что и значения всех остальных неизвестных в е₀ должны быть равны нулю, т. е. что е₀ есть нулевая строка:

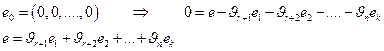
что и требовалось доказать ■

Заметим, что для того чтобы получить фундаментальную систему решений, мы могли бы придавать сво­бодным неизвестным и какие угодно другие значения, лишь бы соответствующий определитель k-ro порядка был отличен от нуля. Так можно найти сколько угодно фундаментальных систем решений, каждая из которых состоит из k = n — r строк. Можно дрказать, что любая фундаментальная си­стема решений уравнений (22) состоит в точности из n — r решений.

Поэтому общее решение системы однородных линейных уравнений имеет вид

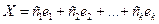, (8.4)

где 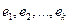какая-то (какая угодно!) фундаменталь­ная система решений, а 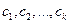- произвольные числа и k = n – r, r- ранг системы.

Из теоремы вытекает алгоритм построения фундаменталь­ной системы решений

1. Найти общее решение однородной системы

2. Выписать диагональную систему (n-r) мерных векторов

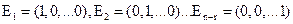
Где r- ранг или число разрешенных неизвестных в общем решении, n- число неизвестных в системе

3. Подставить в общее решение вместо свободных неизвестных координаты вектора 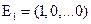, а затем найти значения разрешенных неизвестных. Полученная совокупность значений неизвестных определяет решение .

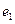4. Аналогично с помощью 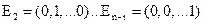найти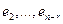

5. Полученные решения образуют фундаменталь­ную систему решений

Найти фундаменталь­ную систему решений однородной системы

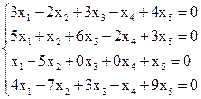
Методом Жордана Гаусса находим общее решение

X1	X2	X3	X4	X5	Таблица
	-2		-1
			-2
	-5
	-7		-1
			-1	-11
			-2	-22
	-5
			-1	-11
	-13	-3
	-5

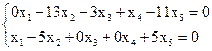
разрешенные неизвестные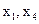

n=5, r=2, n-r=3

Выпишем диагональную систему (n-r) =3 мерных векторов

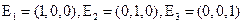
Подставить в общее решение вместо свободных неизвестных 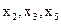координаты вектора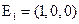

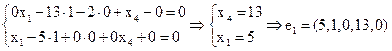
Аналогично

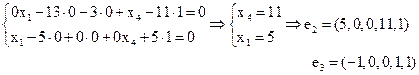
Рассмотрим неоднородную систему линейных уравнений

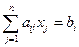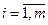, (8.5)

и соответствующую однородную систему линейных уравнений

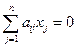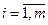, (8.6)

1) Если 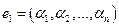- произвольное ре­шение неоднородной системы, а 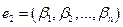- другое ее произвольное ре­шение, то разность 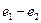будет решение соответствующей однородной системы:

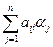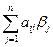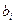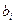- = - =0,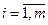

2) Если 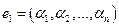- произвольное ре­шение неоднородной системы 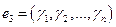произвольное ре­шение соответствующей однородной системы, то сумма 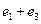будет решением неоднородной системы

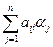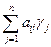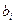+ = + 0,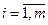

Отсюда следует, что все решения системы (5.3) можно получить, прибавляя к одному какому-нибудь ее реше­нию всевозможные решения однородной системы (5.4).

Вывод: общее решение неоднородной системы линейных уравнений равно сумме общего решения соответствующей однородной системы и про­извольного частного решения неоднородной системы линейных уравнений.

Пример. Решить систему уравнений и найти фундаментальную систему решений

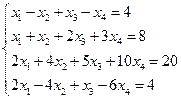
Решение. Решаем методом Жордана- Гаусса

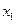
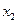
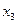
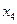
				b	Таблица
	-1		-1
	-4		-6
	-1		-1
	-2	-1	-4	-4
		1,5
		0,5

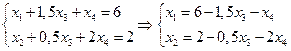
Общее решение неоднородной (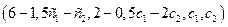

Частное решение неоднородной (6,2,0,0)

Фундаментальная система решений состоит из 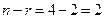уравнений. Придавая последовательно свободным переменным 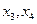тройки чисел (1,0), (0,1,) получаем набор фундаментальных решений

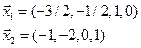
Общее решение неоднородной

■

Х= (6,2,0,0) + +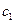

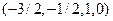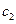
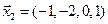
Дата добавления: 2014-01-15