Исследование управляемого движения с помощью передаточных функций

Оценки управляемости различных ЛА принято рассматривать как их реакцию на скачкообразное (ступенчатое) отклонение органов управления и на отклонение по гармоническому закону.

При ступенчатом отклонении изучаются переходные или временные характеристики (функции) ЛА, а при гармоническом - частотные.

Частотные характеристики системы (звена) определяются как зависимость отношения амплитуды выходной величины к амплитуде входного сигнала и сдвига по фазе выходной величины по отношению к входному сигналу от частоты входного воздействия.

При изучении переходных характеристик (процессов) удобно пользоваться передаточными функциями, а частотных характеристик - частотными функциями.

Передаточной функцией называют отношение изображения выходной величины к изображению входной при нулевых начальных условиях:

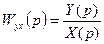. (11.21)

Пример. Пусть задано уравнение, описывающее короткопериодическое движение ЛА, в виде (начальные условия - нулевые):

, (11.22)

здесь: 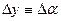или 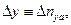Переходя от оригиналов к изображениям, получаем

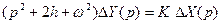(11.23)

и передаточная функция:

(11.24)

Поскольку знаменатель (11.24) составляется по левой части (11.22), то он является характеристическим полиномом дифференциального уравнения (11.22) с той лишь разницей, что вместо l стоит параметр 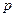.Приравнивая к нулю знаменатель передаточной функции (11.24), получим

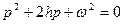(11.25)

Корни этого уравнения называются полюсами передаточной функции или корнями характеристического уравнения (11.22).Если то корни будут комплексными сопряженными

(11.26)

В этом случае будет переходной процесс изменения выходной величины и звено являются колебательными. Если 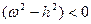, то оба корня будут действительными

.

Процесс будет апериодическим, а звено - апериодическим второго порядка.

Выражая через передаточную функцию (11.24), получим

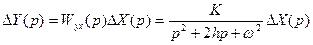. (11.27)

Для определения переходной (временной) функции надо за входное воздействие принять ступенчатую функцию, изображение которой . Следовательно

.

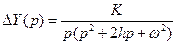По (11.19)

Переходя при помощи таблиц от изображения к оригиналу для случая получим переходную функцию колебательного звена

Δ, (11.28)

где – передаточный коэффициент, – коэффициент демпфирования, – круговая частота колебаний, – опорная частота или частота недемпфированных колебаний, - сдвиг по фазе

. (11.29)

В (11.28) первое слагаемое определяет вынужденное движение, а второе – собственное (свободное) колебательное движение, определяющее переходный процесс.

Рассмотрим пример определения одной из характеристик управляемости, в частности с помощью передаточной функции. Эта производная может быть представлена в видe 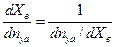.Изображение Лапласа для знаменателя этого выражения

обозначим как передаточную функцию 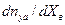=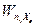.Зададим

входное воздействие в виде ступенчатого единичного 1(t),имеющего изображение

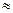
по Лапласу 1/p, и приближенно величину .Передаточная функция в нашем

случае имеет вид 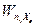= p(p) и в соответствии со свойством (11.19) имеем

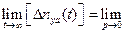
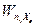(p).

При известной структуре 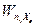(p) можно вычислить (после взятия пределов) установившееся значение выходной величины 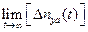=и определить по формуле

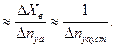
Приведем здесь перечень некоторых из решаемых задач динамики полета с помощью передаточных функций.

I. Используя знаменатель передаточной функции, можно исследовать динамическую устойчивость (по Ляпунову) по первому приближению, т.к. знаменатель по форме совпадает с характеристическим уравнением с той лишь разницей, что вместо «λ» стоит параметр «p».

II. Если в качестве входного воздействия принять в (11.22), то изображение по Лапласу 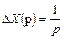и W(p) = p Y(p) можно использовать для определения установившегося значения переходной функции y(t) на основе теоремы 2) (11.19), т.к. .

III. При построении систем автоматического управления (САУ) изучаются

передаточные функции «замкнутых» систем, являющихся функциями исходных W(p) и проблема сводится к выбору параметров САУ такими, чтобы характеристики устойчивости и управляемости ВС были оптимальными, удовлетворяющими нормативным документам (АП –23, 25 и др.).

IV. Для устойчивых систем от W(p) нетрудно перейти к частотным характеристикам, положив p = iω и исследовать показатели («запасы») устойчивости и управляемости по АФЧХ.

V. Некоторые из показателей статической управляемости можно вычислить непосредственно по W_yx(p).

VI. С помощью перехода от изображений к оригиналам нетрудно перейти к исследованиям во временной области.

В заключении заметим, что обычно для ВС составляются перечни (таблицы, «библиотека») передаточных функций, которые широко используются при решении различных задач динамики полета.

Дата добавления: 2014-01-15