Пример 5.Сколько существует размещений с повторениями при выборке k шаров из n?

Решение. Так как по определению любой из k шаров в размещениях может быть повторен от 1 до k раз, то всего вариантов выбора есть n^k, то есть имеет место простой случайный выбор (см. пример 1).

Пример 6. Сколько существует сочетаний с повторениями при выборе k шаров из n?

Решение. Расположим n шаров на прямой и ограничим их слева и справа вертикальными черточками | 00... 0| (шару соответствует 0).

Возьмем еще (k -1) черточку и произвольно распределим черточки между шарами, причем, между соседними шарами может находиться одна или более черточек. Интерпретируя две соседние черточки как ящик, получим, что число шаров между соседними черточками – это число повторных шаров в ящике. Перечисляя возможные расположения (k - 1) черточек между шарами, получим число сочетаний с повторениями.

Итак, задача свелась к следующей: имеется (n + k - 1) – мерный вектор, координаты которого состоят из n шаров и (k - 1) черточек. Так как число способов расположения (k - 1) черточек по (n + k - 1) месту равно (см. пример 4), то это и есть искомое число вариантов выбора k шаров из n с повторениями.

Замечание. Формула сочетаний с повторениями используется, например, при подсчете числа решений (в целых числах, включая ноль) диофантова уравнения

.

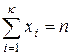Число m частных производных порядка k от функции n переменных также вычисляется по формуле .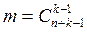

Приведем некоторые свойства сочетаний.

Рассмотрим бином Ньютона

, (1)

где , 0! = 1.

Благодаря формуле бинома Ньютона, сочетания иногда называют биномиальными коэффициентами.

Если в (1) а = b = 1, то получаем

,

если а = - b, будем иметь

.

Если k £ n, то для вычисления сочетаний имеем формулу

.

В самом деле,

._▼

Отсюда следует, что

.

Для любого целого k и n имеем

.

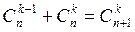В самом деле,

._▼

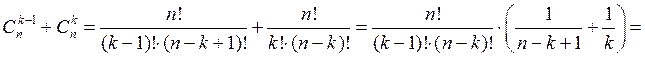
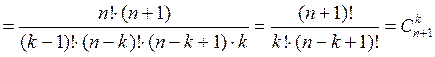Пример 7. В урне находятся n пронумерованных шаров, из которых k красные и (n - k) черные. Наудачу выбираем без возвращения r шаров. Сколько различных выборок объема r можно получить, если среди выбранных r шаров s – красных?

Решение. Разделим урну условно на две половины так, что в одной находятся k красных шаров, а в другой (n - k) черных. Среди k красных шаров s шаров можно выбрать 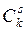способами, а среди (n - k) черных шаров (r – s) шаров можно выбрать способами. Поскольку на каждую фиксированную выборку красных шаров приходится выборок черных, то всего выборок объема r будет , .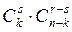

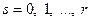Замечание. Если в предыдущей задаче мы выбирали бы r шаров из n без учета их цвета, то всего различных выборок было бы . С другой стороны, если учесть все возможные варианты выбора красных шаров s, то получаем, что всего их будет .

Таким образом, имеем формулу

.

Дата добавления: 2014-01-15