Методи інформаційно-логічного аналізу

Метод порівняння. Порівняння — найбільш по­ширений метод проведення економічних досліджень, який полягає у зіставленні однорідних об'єктів з ме­тою знаходження подібних або різних елементів. По суті з нього розпочинається аналіз роботи підпри­ємств, галузі, результатів реалізації економічної полі­тики.

В економічних дослідженнях застосовуються та­кі види порівнянь: з планом, попереднім періодом, нормативом, з іншими однопрофільними {кращими, гіршими, найбільш типовими) або суб'єктами, еко­номічною моделлю, середньогалузевими та регіо­нальними показниками, різними варіантами вирі­шення економічного завдання і т. п.

При порівнянні звітних даних з плановими звер­тається увага на обґрунтованість і напруженість планових завдань. Критичний аналіз плану дає змо­гу з'ясувати причини відхилень реальних показ­ників. Планові завдання мають відповідати наявним матеріально-технічним, трудовим та іншим ресур­сам, можливостям використання господарського і природного потенціалів, бути зіставними з показни­ками порівнюваних підприємств.

Порівняння показників у часі, тобто звітних да­них з показниками попередніх періодів, дає мож­ливість оцінити темпи розвитку підприємств у ди­наміці. На основі аналізу минулого і теперішнього станів можна зробити відповідні висновки на май­бутнє.

Порівняльний аналіз підприємницької діяль­ності окремого підприємства з іншими дає змогу встановити його місце в сукупності однопрофільних підприємств регіону або галузі за масштабом, рівнем організації, базовими економічними і фінансовими показниками, темпами та напрямками розвитку, визначити кращі економічні показники та шляхи їх досягнення.

Порівняння з економічною моделлю в ідеальних умовах дає можливість визначити, якою мірою пев­ний суб'єкт наближається до розрахунково-конст­руктивного рівня використання ресурсів або соці­ально-економічної ефективності. Такий вид порів­няльного аналізу сприяє правильному оцінюванню поточного стану системи та визначенню строків до­сягнення поставлених завдань.

Порівняння з найкращим аналогом (внутріш­ньогосподарським підрозділом, підприємством, ре­гіоном, країною) дає змогу виявити організаційні та економічні резерви, які слід задіяти для покращан­ня ситуації.

Внутрішньогалузеве порівняння однотипних під­приємств, як правило, показує резерви комплекс­ного підвищення ефективності виробництва і послуг, оскільки свої висновки будує на результатах вивчен­ня досвіду багатьох підприємств.

Порівняльний аналіз також: застосовується в ме­жах регіонів та для міжнародних зіставлень. Для цього проводиться порівняння узагальнюючих одно­типних показників регіонального розвитку і країн в цілому за технічними, економічними, технологічни­ми, соціальними, екологічними характеристиками.

Обов'язковою умовою порівняння є повна зіставність показників за критеріями предметного змісту, типу виробництва, форм власності і господарюван­ня, методології планування, обліку і калькуляції, виду продукції (валова, товарва, чиста), одиниць вимі­рювання, галузей, цін тощо.

Приведення даних до зіставного вигляду досяга­ється шляхом відбору та відповідної обробки показ­ників, перерахуванням даних за єдиною методикою, приведенням їх до тотожних одиниць вимірювання, відокремленням однорідної сукупності, заміною аб­солютних величин на відносні, застосуванням різно­го роду коефіцієнтів, інтегральних показників.

Методи розрахунку відносних та середніх вели­чин. Будь-які процеси, що відбуваються в економіці, можна охарактеризувати за допомогою абсолютних та відносних величин. Абсолютними є такі, що кількісно відображають розміри певного предмета або явища безвідносно до його структури та інших об'єктів (наприклад, вартості, ваги, обсягу, трива­лості тощо), тоді як відносні застосовуються саме для зіставлення величин різних предметів або явищ, взятих в узгодженій системі координат (коефіцієн­ти, відсотки, частки тощо).

Абсолютні показники це, як правило, резуль­тати первинного спостереження за економічними процесами. Вони є базою для розрахунку відносних. Серед відносних величин, які застосовуються най­більш широко у процесі аналізу, слід назвати від­носні величини (проектного) планового завдання, виконання плану, динаміки, структури, координа­ції, інтенсивності та ефективності.

Середні величини широко застосовуються при проведенні економічних досліджень для узагальнен­ня маси однорідних явищ і виявлення закономірно­стей на основі спостережень.

Середні величини — це типові розміри кількісно варіюючих ознак якісно однорідних явищ, процесів.

У такому розумінні середня є рівнодіючою впливу всіх факторів на величину ознаки. Щоб середня ве­личина характеризувала типові розміри сукупності об'єктів, потрібно враховувати такі вимоги:

— досліджується множина якісно однорідних об'єктів;

— кількість об'єктів має бути достатньо великою;

— ознака повинна бути істотною.

Кількісні закономірності розвитку суспільних явищ і процесів рельєфно проявляються лише за знач­ної кількості спостережень: чим більше однорідних одиниць одного явища в сукупності, тим точніше про­являються їх типові якості. При роботі зі значними групами або результатами численних спостережень випадкові відхилення від закономірностей, тобто се­редньої величини, взаємно погашаються. Тому се­редні розрахункові величини стають типовими, відоб­ражаючи вплив постійних істотних факторів. Завдан­ня дослідника полягає в тому, щоб за результатами обстеження групи вивести певні закономірності, за якими можна судити про явище в цілому.

Залежно від характеру усередненої ознаки і на­явних даних в економічних дослідженнях використо­вуються: середня арифметична, середня гармоній­на, середня геометрична, мода, медіана та інші.

Середня арифметична може бути простою і зва­женою. Середня арифметична проста розраховуєть­ся як сума окремих значень, поділена на їх число:

Середня арифметична зважена застосовується тоді, коли конкретні значення ознаки (варіанти) мають різне число одиниць спостереження або роз­раховується середня із середніх. Це дає змогу про­вести групування і побудувати варіаційний ряд роз­поділу, в якому наводяться значення ознаки (варі­ант) та кількість одиниць (вага або повторюваність), що мають однакову величину досліджуваної ознаки.

Для розрахунку середньої зваженої немає потре­би механічно розраховувати суму чисельника, як це робиться для середньої арифметичної простої. Той самий розрахунок буде більш досконалим, а резуль­тат — тим самим, що і при застосуванні формули 6.1. Для цього потрібно суму множин індивідуаль­них значень базової ознаки, що усереднюється, а їх повторюваності поділити на сумарну кількість та­ких повторів (явищ):

де — середнє значення;

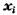— величина або характеристика ознаки, що підлягає усередненню;

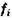— кількість одиниць, що мають відповідну характеристику ознаки (вага або повторюваність);

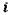— сукупна кількість досліджуваних одиниць множини;

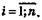
Застосування для одних і тих самих даних фор­мул 6.1 та 6.2 дасть єдиний результат. Він не збі­гається з індивідуальними величинами досліджуваної множини, але завжди знаходиться у проміжку між мінімальним і максимальним значеннями.

Поряд із середньою арифметичною досить часто застосовують середню гармонійну, яка також може бути простою і зваженою.

Середня гармонійна — це величина, зворотна середній арифметичній, складена зі зворотних зна­чень досліджуваної ознаки. її застосовують у випад­ках, коли вагу потрібно не множити, а ділити на варіанти (тобто множити на зворотні величини) — коли не відомо чисельності сукупності, а для отри­мання результату необхідно зважувати варіанти за обсягами досліджуваної ознаки. При цьому слід па­м'ятати, що всі проміжні дії під час розрахунку се­редньої повинні давати економічно обґрунтовані по­казники (6.3—6.4):

Де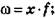

— середнє значення варіюючого показника;

— ознака, за якою ведеться дослідження;

— вага варіантів;

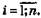
Кожен елемент формул 6.3 і 6.4 повинен підда­ватись економічній інтерпретації, чого, власне, і вимагають правила розрахунку середньої гармоній­ної.

Формула середньої гармонійної простої скла­дається зі зворотної величини усереднюваного по­казника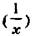та значення повторюваності (га):

На відміну від наведених раніше показників, се­редня геометрична розраховується тоді, коли логі­ка потребує не складання значень усередненого по­казника, а множення індивідуальних значень тієї ознаки, що досліджується (6.6—6.7):

де п — кількість індивідуальних значень усередню­ваної ознаки; або

(6.7)

Де

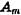— кінцевий абсолютний показник ряду;

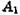— початковий абсолютний показник ряду;

— кількість рівнів ряду.

Середня геометрична — найбільш уживаний по­казник для розрахунку середніх показників дина­міки, який частково абстрагуючись від флуктуацій (коливань) окремих років дає змогу судити про загаль­ну тенденцію — темпи зростання або приросту.

Необхідно окремо наголосити, що при користу­ванні методом розрахунку середніх величин надзвичайно важливе значення має правильність вибору її типу. Для цього слід встановити визначальний по­казник (х), на який орієнтований весь розрахунок 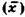, а потім вибрати формулу (6.1—6.7). Головне питання такого вибору — визначення невідомої за двома відомими величинами.

Арифметична середня, як правило, застосовуєть­ся, якщо відомі первинні дані про чисельник і зна­менник або про ознаку і її вагу.

Гармонійна середня розраховується, якщо відомі ознака й один із показників кількісного співвідно­шення.

Причому, якщо у нашому розпорядженні про­стий перелік одиниць і значень усереднюваної озна­ки, то слід вдатись до простої арифметичної або гео­метричної середньої, а якщо маємо ряд розподілу (варіанти та їх повторюваність), необхідно користу­ватись зваженою середньою арифметичною чи гео­метричною.

Середні величини також можуть бути визначені у принципово інший спосіб, ніж описано вище. Для цього користуються модою і медіаною.

Мода — це значення ознаки варіаційного ряду, що найбільш часто трапляється, тобто варіант ряду, що має найбільшу вагу або частоту.

Медіана — це значення досліджуваної ознаки певної сукупності, яке знаходиться всередині зрос­таючого варіаційного ряду або такого, що зменшу­ється.

Такі показники, як мода і медіана, мають вели­ке значення для економічного аналізу, оскільки доз­воляють визначити найбільш поширене явище (мода) та чітко поділити всю сукупність на дві частини, що знаходяться вище та нижче певного рівня (се­редини). Це дуже корисно при виявленні невикори­станих резервів та виборі найбільш ефективних управлінських рішень.

Дата добавления: 2014-01-11