Методи стохастичного (кореляційного) факторного аналізу

Методи кореляційного аналізу. Для того щоб отри­мати достовірні відомості про предмети та явища навколишнього світу, зокрема ті, що відбуваються у сфері економіки, необхідно пам'ятати, що всі вони мають внутрішнє і зовнішнє середовище, з яким перебувають у діалектичній єдності — отримують від них певний вплив та самі на них впливають. Отже, досліднику важливо знати, які елементи справляють найсуттєвіший вплив і який саме його характер. Для цього застосовують поняття "функ­ціональні зв'язки", "кореляційні зв'язки" та відпо­відні методи їх оцінювання.

Незалежно від того, маємо ми справу з функціо­нальними чи кореляційними зв'язками, їх слід поді­ляти на:

— прямі (напрямок зміни ознаки та результую­чого показника збігаються) та зворотні (напрямок зміни ознаки та результуючого показника є проти­лежними);

— лінійні (зі зростанням факторної ознаки без­перервно змінюється (збільшується або зменшуєть­ся) результуюча) або нелінійні (у разі зростання фак­торної ознаки результуюча змінюється нерівномір­но або змінюється напрямок);

— однофакторні (досліджується зв'язок між од­нією ознакою (фактором) та результатом) та багатофакторні (маємо декілька ознак, які впливають на кінцевий результат). Це, відповідно, парна та мно­жинна кореляції.

Функціональний зв'язок — це такий тип взає­мозалежності результуючого показника й ознаки, коли одному значенню ознаки відповідає лише одне значення результату. Він найбільш широко засто­совується у фізиці, математиці, точних науках, тоді як в економіці трапляється значно менше. Функціо­нальний зв'язок за своїми ключовими характери­стиками є повним, точним, відображає однозначний вплив усіх факторів на результат та з однією силою проявляється щодо всіх одиниць досліджуваної су­купності.

Як уже наголошувалось, дослідження функціо­нальних зв'язків відбувається за допомогою ряду методів, серед яких найбільш поширені балансовий та індексний.

При вивченні явищ, які мають місце у суспіль­ному та економічному житті, зазвичай нам відома лише частина факторів, їх іноді неповний взаємо­зв'язок, основні види впливу. У такому разі засто­совують комплекс методів дослідження кореляцій­них зв'язків. Вони відображають неповний зв'язок між ознаками і результуючим показником, що має загальний або усереднений характер, і потребують для свого виявлення масових спостережень, підпа­даючи під дію закону великих чисел.

Дослідження кореляційних зв'язків потребує від дослідника володіння такими методами: взаємної залежності (для атрибутивних (якісних) ознак); па­ралельних рядів (для кількісно варіюючих ознак); кореляційно-регресивного аналізу, а також графіч­ного, аналітичних групувань тощо.

Розглянемо основні положення методів вивчен­ня кореляції атрибутивних ознак, однофакторного та багатофакторного кореляційних аналізів.

Сутність однофакторного кореляційного аналі­зу полягає у побудові та подальшому вивченні мо­делі, яка наближається до реальної залежності між ознакою-фактором та результатом. Для цього спо­чатку проводять теоретичний аналіз, спрямований на обґрунтоване визначення: по-перше, того, чи пра­вильно обрано фактор; по-друге, чи справді існує певний причинно-наслідковий зв'язок між ним і ре­зультатом; по-третє, який характер може мати цей зв'язок — прямий/зворотний, лінійний/нелінійний тощо. Далі за допомогою графічного метода зобра­жується масив даних (ознака-фактор), здійснюєть­ся вирівнювання лінії регресії та за допомогою якіс­ного аналізу визначають форму зв'язку (лінійний зв'язок, нелінійний зв'язок — гіпербола, парабола, логарифмічна). Розраховують коефіцієнт регресії, коефіцієнт еластичності та індекс кореляції.

Багатофакторний кореляційно-регресивний аналіз дає змогу нам оцінити ступінь впливу на ре­зультуючу ознаку кожного із введених у модель фак­торів за умови фіксації інших: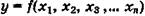Тут також збирається вихідний статистичний мате­ріал (результати спостережень), визначається форма зв'язку (емпіричним шляхом, за аналогією та ін.), який переважно зводиться до лінійної форми:

Далі визначаються парні, часткові (окремі) кое­фіцієнти кореляції, сукупні коефіцієнти множинної кореляції та детермінації.

Кореляційно-регресивний аналіз знаходить своє застосування під час оцінювання резервів виробниц­тва, побудови програм розвитку, порівняльного ана­лізу, короткострокового прогнозування тощо.

Метод порівняння паралельних рядів. Порівнян­ня паралельних рядів є одним із методів дослідження кореляційної залежності, який дає змогу наочно оці­нити зв'язки між показниками, що кількісно зміню­ються. Для того щоб застосування цього методу дало адекватний результат, який би досить точно відобра­жав реальний стан речей, необхідно провести по­передній теоретичний аналіз. Такий аналіз дає змогу встановити можливість існування та сутність зв'язків, їх характер. Надалі фактори, що характеризують ре­зультуючу ознаку, слід розташувати у порядку зрос­тання або зменшення. Виявляють, чи має місце зв'я­зок та яка його спрямованість, характер, повнота.

Для характеристики напрямку і тісноти зв'язків у статистиці зазвичай застосовують коефіцієнт Фехнера, який порівнює знаки відхилення досліджува­них ознак (х, у) від середньої арифметичної (х, у). При цьому '*+" означає, що розмір певної ознаки пе­ревищує середню, а "-", навпаки, є меншим. Збіг знаків приводить дослідника до висновку про узго­джену варіацію.

Коефіцієнт Фехнера розраховується за форму­лою (6.27), має значення у проміжку між "-1" (пов­ністю узгоджена зворотна залежність) та "+1" (пов­ністю узгоджена пряма залежність), тоді як "0" до­водить, що залежність повністю не узгоджена.

де С — кількість збігу знаків, Н — кількість незбігу знаків.

Застосування цього коефіцієнта дає лише загаль­ну (принципову) оцінку наявності та характеру зв'язку, тоді як його силу можна визначити за допомогою коефіцієнта кореляції рангів, що також змінюєть­ся у проміжку між "-1" (повна зворотна кореляція рангів) та "+1" (повна пряма кореляція рангів), тоді як "0" доводить, що кореляція рангів відсутня.

де — різниця рангів;

— кількість одиниць сукупності.

Дата добавления: 2014-01-11