Эквивалентное напряжение и критерии предельного состояния

Обозначим как «состояние A» любое заданное сложное напряженное состояние, которое задается главными напряжениями σ ₁, σ ₂ и σ ₃ (рис. 6.2, а). Как «состояние B»обозначим такое одноосное напряженное состояние, которое равноопасно состоянию А (рис. 6.2, б). Число, которое показывает во сколько раз надо увеличить все компоненты напряженного состояния, чтобы оно стало предельным, называют коэффициентом запаса. Напряженные состояния А и В, имеющие одинаковые коэффициенты запаса, называются равноопасными состояниями.

Рис. 6.2. Два напряженных состояния: заданное сложное (А)

и одноосное эквивалентное (В)

В таком случае напряжение растяжения, возникающее в частице В, называют эквивалентным напряжением. Другими словами, эквивалентнымназывают такое напряжение 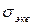, которое следует создать в растянутом образце, чтобы его состояние(состояние В) и заданное состояние(состояние А) были равноопасны. На этом основании расчет в условиях сложного напряженного состояния сводится к расчету при простом растяжении. Если каким-то образом для состояния A будет найдено значение , то его необходимо сопоставить с напряжением 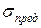для данного материала (пределом текучести или пределом прочности) и определить коэффициент запаса. Поэтому, в символической записи, условие прочности имеет вид следующего неравенства

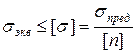, (6.1)

где 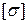— допускаемое напряжение, 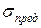— предельное напряжение (определяемое из испытаний на растяжение), [ n ]–– нормативный коэффициент запаса.

Вопрос теперь состоит в том, как выразить через главные напряжения σ ₁, σ ₂ и σ ₃. Если мы сумеем этого добиться, то задачу об оценке прочности можно считать решенной. С этой целью делается предположение о причине наступления предельного состояния. В качестве такой причины, из чисто физических соображений, назначается некоторый фактор (критерий), который считается одинаковым для всех мыслимых напряженных состояний. Например, если материал сопротивляется разрыву волокон хуже, чем сдвигу, то за критерий прочности принимаются величины нормальных наибольших напряжений или линейных деформаций, т. е. 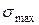или 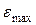. И наоборот, если материал хуже сопротивляется сдвигу, то за критерий перехода в предельное состояние принимается величина наибольшего касательного напряжения 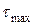или удельная энергия изменения формы 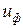частицы тела.

Дата добавления: 2014-01-15