Пример решения задачи

Уравнения Лагранжа II рода описывают не только механические движения но и, нередко, движения немеханической природы.

по исследованию свободных колебаний механической системы с одной степенью свободы. Задание Д-23. вариант №16

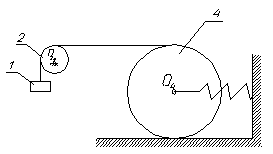
Дано: механизм приводится в движение грузом 1 до момента, когда противодействие пружины его не остановит. После этого механизм совершает свободные колебания под действием силы веса груза 1, инерционных сил всех звеньев и силы упругости пружины. Массы звеньев: m₁=1кг, m₂=2кг, m₄=3кг, Жёсткость пружины с=32н/см.

Начальное положение (соответствующее статической деформации пружины) и скорость груза 1, взятые в проекции на ось Y: y₀=0,3см,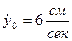

Определить:

1) частоту (к) и период (Т) малых свободных колебаний механической системы с одной степенью свободы, пренебрегая силами сопротивления и массами нитей.

2) найти уравнение движения груза 1 y=y(t), приняв за начало отсчета положение покоя груза 1 (при статической деформации пружины).

3) найти амплитуду (а) колебаний груза 1.

Решение:

1. Воспользуемся уравнением Лагранжа II рода для консервативной системы (уравнение (23)), приняв за обобщённую координату системы вертикальное отклонение груза 1 от положения покоя (y), соответствующего статической деформации пружины, Имеем следующее уравнение:

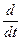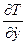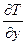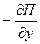() - = где Т – кинетическая энергия системы; П – потенциальная энергия системы.

В общем случае кинетическую энергию Т вычисляем с точностью до величин второго порядка малости относительно 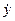и 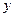, а потенциальную энергию П – с точностью до величин второго порядка малости относительно обобщённой координаты 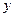. (В приведенном примере задачи в этом нет необходимости)

2. Найдём кинетическую энергию системы, равную сумме: Т=Т₁+Т₂+Т₄

2.1. Для этого составим кинематические уравнения связи скоростей звеньев механизма в зависимости от 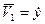и :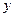

; ; ; ; ;

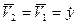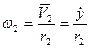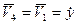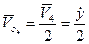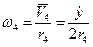2.2. Найдём моменты инерции тел, входящие в уравнения кинетической энергии:

; ;

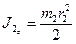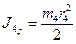2.3. Определим кинетические энергии звеньев механической системы:

; ;

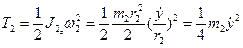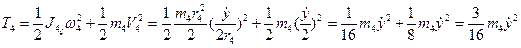
2.4. Определим кинетическую энергию системы в целом:

Т=Т₁+Т₂+Т₄=++=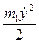

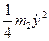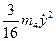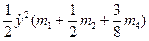
3. Найдем П – потенциальную энергию системы тел, которая определяется работой сил тяжести звеньев системы и силы упругости пружины на перемещении звеньев системы из отклонённого положения, когда груз имеет координату 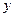, в нулевое положение, которым считаем положение покоя системы:

П = П₁ + П₂

3.1. Найдём потенциальную энергию звеньев, вызванную работой сил тяжести П₁:

П₁ = -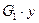

3.2. Найдём потенциальную энергию, вызванную работой пружины (при возврате «домой» из отклонённого положения) П₂: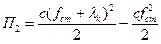

Найдём 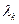- динамическое растяжение пружины, вызванное перемещением 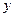груза 1:

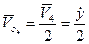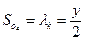так как то ; где 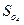- перемещение пружины и центра тяжести диска 4 (точки О₄). Тогда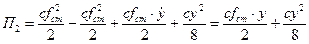

3.3. В целом потенциальная энергия системы равняется:

П = П₁ + П₂= - +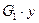

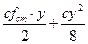
Рассмотрим два варианта упрощения формулы потенциальной энергии системы:

1-й вариант: определим частную производную П по y:

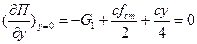(то есть производную мы определили при y=0 в положении покоя системы, соответствующем статической деформации пружины).

Тогда: 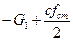=0

2-й вариант: определим сумму моментов всех сил относительно МЦС₄ (мгновенного центра скоростей звена 4) для положения покоя системы: 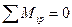или: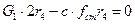

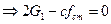
То есть в обоих вариантах мы получили одинаковый результат: 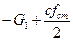=0

Вычленим этот двучлен из уравнения потенциальной энергии:

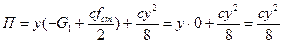
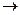
4. Составим уравнение Лагранжа II рода, выполнив операции дифференцирования Т и П:

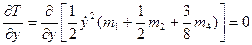
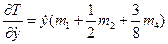
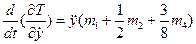
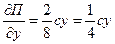
Мы определили все составляющие уравнения Лагранжа. Сложим их:

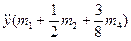- 0 = - ;

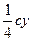Преобразуем это уравнение Лагранжа II рода, которое приобрело вид линейного уравнения второго порядка с постоянными коэффициентами без правой части (см. справочник Выгодского стр.845):

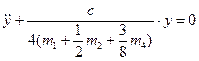
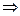
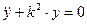(А)

мы получили линейное уравнение второго порядка с постоянными коэффициентами без правой части из которого находим все искомые величины.

5. Определим циклическую частоту свободных колебаний системы «К»:

коэффициент при «y» является квадратом циклической частоты свободных колебаний системы:

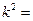
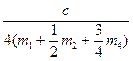или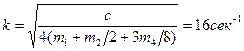

6. Период свободных колебаний системы (значёк совпадает со значком кинетической энергии – но не более того) равен: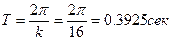

7. Найдем уравнение движения груза 1, проинтегрировав уравнение (А): 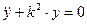его характеристическое уравнение (см справочник Выгодского) 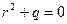(общий вид этого характеристического уравнения по Выгодскому )

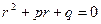Определим к какому случаю решения относится этот вид уравнения: 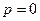тогда 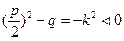Вывод: это III случай линейного уравнения 2-го порядка без правой части. Формула уравнения движения для этого случая имеет вид:

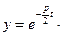(C₁cosβt+C₂sinβt) (В) где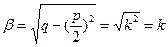

Тогда уравнение движения (В) примет вид: y=C₁coskt+C₂sinkt (C)

Определим коэффициенты С₁ и С₂, исходя из того, что нам известны начальные условия кинематического состояния системы (в частности начальные положение и скорость груза 1 - 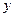и 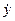): находим уравнение скорости груза 1, продифференцировав уравнение (С): 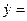- kC₁sinkt + kC₂coskt (D)

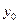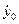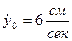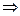Подставим в уравнения (С) и (D) значения и при t=0. Получим искомые коэффициенты С₁ и С₂: y₀=0,3см=C₁, =kC₂ C₂=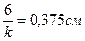

тогда уравнение движения груза 1 (С) примет окончательный вид:

y=0,3coskt + 0,375sinkt

8. Определим амплитуду «а» свободных колебаний груза 1:

Выразим уравнение колебательных движений в форме объективно показывающей амплитуду колебаний: y=asin(kt+β) (Е)

Здесь амплитуда объективно выражена и равняется: .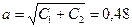

Начальная фаза смещения амплитуды колебаний:

β=arctg(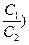= arctg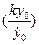=39⁰=0,68 радиан.

Тогда окончательно уравнение движения груза 1 в форме (Е) примет вид:

y=0,48sin(16t + 0,68)

_________________________________________________________________________

Справочная информация:

Вычисление Т, П и Ф в обобщённых координатах

Пусть система состоит из «n» точек и имеет «s» степеней свободы.

Кинетическая энергия системы:

T=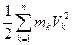, так как 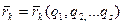но 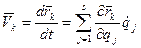, тогда кинетическая энергия будет равна: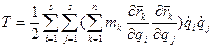

назовём в этой формуле множитель в скобках: 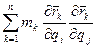= 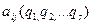коэффициентом инерции. Тогда уравнение кинетической энергии примет вид:

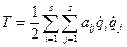при s=1 получим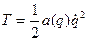

Рассмотрим потенциальную энергию системы:

П=П(q_1, q_2, …q_s) разложим её в ряд Маклорена:

П=П(q_1, q_2, …q_s)=П(0, 0, …0) +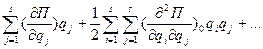

Принимаем П(0, 0, …0)=0, тогда 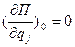выражает состояние равновесия.

П=П(q_1, q_2, …q_s)= где C_ij=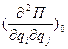 коэффициент жёсткости

Потенциальная энергия П=, При s=1 П=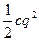

Функция рассеивания энергии (функция Релея)

Рассмотрим случай, когда сила сопротивления среды, что воздействует на к -тую точку системы, равна .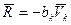

Тогда обобщённая сила сопротивления, соответствующая 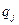обобщённой координате, будет равна:

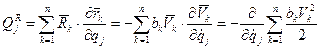
где 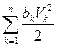=Ф – функция рассеивания или функция Релея.

Структура Ф (функции рассеивания) такая же как у Т (кинетической энергии), а потому 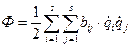, где 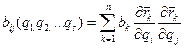, если s=1 то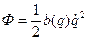

Понятие устойчивого равновесия механической системы.

Критерий устойчивости Лагранжа – Дирихле.

Равновесие бывает устойчивым, неустойчивым и безразличным.

Критерий:

Пусть все связи механической системы голономные, идеальные, стационарные и удерживающие, а все заданные силы – консервативные.

Пусть в некотором положении S^* системы потенциальная энергия системы имеет строгий минимум, а мгновенные скорости всех точек системы равняются нулю.

Тогда S^* - это положение устойчивого равновесия системы.

Это достаточное условие.

Два классических условия неустойчивого равновесия были показаны Ляпуновым. Этим вопросом занимался также и Чатаев.

Дата добавления: 2014-01-15