Уравнения Лагранжа II рода (когда s – конечное число) есть обыкновенные дифференциальные уравнения

Лагранж построил динамику на основе скалярной меры движения механической системы – кинетической энергии: и эта мера механического движения потребовала введения понятия работа силы - как меры силы.

В методике Лагранжа механическую систему рассматривают как одно целое, отдельные материальные точки системы не выделяются. Уравнения Лагранжа II рода показывают скорость изменения меры движения системы (кинетической энергии).

Сравнивая (А) и(В) 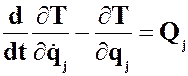можно объяснить преобразования, которые выполнялись затем над уравнением (6) при переходе общего уравнения динамики в виде работы ньютоновых сил (меры выражения движения по Ньютону) в дифференциальные уравнения кинетической энергии второго порядка (меры выражения движения по Лагранжу) в обобщённых координатах (в уравнения Лагранжа второго рода).

2. Количество уравнений движения системы, как видно из (В), будет столько, сколько степеней свободы имеет механическая система, и, в случае голономных реакций связи, равняется числу обобщённых координат S. Их количество не будет зависеть от количества точек «n», входящих в систему. Для уравнения Лагранжа I рода:

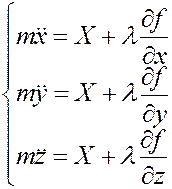, где - множитель Лагранжа

всё наоборот - (количество уравнений зависит от количества точек «n», входящих в систему), что является одной из причин введения обобщённых координат. Из общего уравнения динамики (2) явно не видно количества уравнений движения.

3. Уравнения Лагранжа II рода исключают из уравнений реакции идеальных связей и это позволяет вторую задачу динамики разложить на два этапа:

а) вначале найти закон движения . Дифференцируя дважды уравнение движения мы находим ускорение 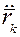k-той точки.

б) затем, зная 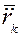, приложенные к системе силы и массу , можем определить реакции неизвестных связей из уравнения: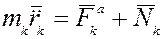

4. Форма уравнений Лагранжа II рода не зависит от конкретного выбора обобщённых координат и принципиально важно:

уравнения Лагранжа II рода сохраняют свою форму и тогда, когда обобщённые координаты характеризуют положение материальной системы в неинерциальной системе отсчёта. (так как не оперируют понятиями сил инерции)

5. Преимущество уравнения Лагранжа II рода перед общим уравнением динамики состоит в том, что при его применении нужно работать только со скоростями, в то время как в общем уравнении динамики нужно работать с ускорениями, что труднее (так как повышается порядок дифференцирования и интегрирования).

6. Методика применения уравнений Лагранжа II рода проста:

а) определить число степеней свободы,

б) ввести обобщённые координаты,

в) вычислить обобщённые силы,

г) вычислить кинетическую энергию,

д) выполнить простые действия и получить дифференциальное уравнение движения.

Эта последовательность действий называется Лагранжевым формализмом.

Дата добавления: 2014-01-15