Выражение обобщенных сил через проекции сил на неподвижные оси декартовых координат. Случай сил, имеющих потенциал

Обобщенной силой,соответствующей обобщенной координате, называют скалярную величину, определяемую отношением элементарной работы действующих сил, на перемещении механической системы, вызванном элементарным приращением координаты, к величине этого приращения.

Равенство (119.1) можно представить в виде 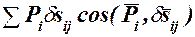(119.2)

откуда следует, что произведение обобщенной силы, соответствующей координате , на приращение этой координаты 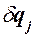, равно элементарной работе приложенных к системе сил на перемещении системы, вызванном приращением этой координаты.

Из формулы (119.2) видно, что размерность обобщенной силы зависит от размерности соответствующей обобщенной координаты:

Так, например, линейной обобщенной координате q соответствует обобщенная сила Q, измеряемая единицами силы.

Если за обобщенную координату q принять угол φ, измеряемый в радианах, то размерность обобщенной силы Q совпадает с размерностью момента [н∙м]. Так как каждой обобщенной координате соответствует обобщенная сила, то число обобщенных сил механической системы равно числу обобщенных координат, причем размерность каждой из обобщенных сил соответствует размерности соответствующей обобщенной координаты. Известно, что существует два способа группировки сил, действующих на механическую систему:

1) деление на внешние и внутренние силы;

2) деление на задаваемые силы и реакции связей.
Соответственно этому обобщенные силы разделяются или на обобщенные внешние и обобщенные внутренние силы или на обобщенные задаваемые силы и обобщенные реакции связей.

Покажем, что в случае стационарных связей обобщенные реакции идеальных связей равны нулю. Действительно, для нахождения обобщенной реакции, соответствующей координате следует вычислить сумму работ реакций связей на перемещении системы, соответствующем приращению 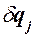этой координаты, а затем определить обобщенную реакцию связи по формуле

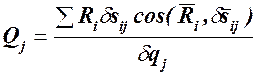
Как указывалось выше (§ 113), в случае стационарных связей описанное перемещение системы является одним из возможных перемещений этой системы, а потому сумма работ реакций идеальных связей на этом перемещении равна нулю, т.к. :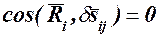

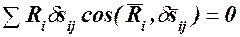
отсюда следует, что (j=1,2,…,s) (119.3)

Таким образом, при определении обобщенных сил, реакции идеальных связей выпадают.

Рассмотрим примеры вычисления обобщенных сил.

Пример 76. Рычаг АВ вращается вокруг горизонтальной оси, проходящей через точку О, перпендикулярно к плоскости рисунка (рис. 259).

К концам рычага приложены вертикальные силы P₁ и Р₂; ОА = а, ОВ = b. Приняв угол φ, определяющий положение рычага, за обобщенную координату, определить соответствующую ей обобщенную силу.

Решение: Для нахождения обобщенной силы Q_φ, соответствующей обобщенной координате φ, сообщаем координате φ приращение δφ (рис. 259). Отмечаем элементарные перемещения, которые получают при этом точки приложения сил Р₁ и Р₂. Эти перемещения направлены перпендикулярно к отрезкам О А и ОВ и равны: δs₁ =aδφ и δs₂=bδφ

Составляем сумму работ сил Р₁ и Р₂ на перемещениях и 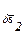, вызванных приращением угла поворота рычага φ:

Подставляем значения перемещений и :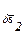

Обобщенную силу 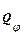определяем по формуле (119.1) как отношение работы к приращению координаты δφ:

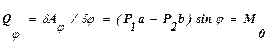
Полученный результат показывает, что обобщенная сила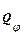, соответствующая углу φ, равна главному моменту сил, приложенных к рычагу, относительно опорной точки О.

Пример 77. Центробежный регулятор вращается вокруг вертикальной оси. Вес каждого шара регулятора равен G, вес остальных частей может не учитываться. Длины стержней равны l. Приняв за обобщенные координаты угол α, образованный стержнями регулятора с вертикалью, и угол поворота регулятора φ вокруг вертикальной оси, найти обобщенные силы, соответствующие этим обобщенным координатам.

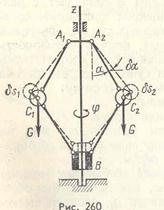
Решение. Для нахождения обобщенной силы , соответствующей обобщенной координате α (рис. 260), сообщаем углу α приращение δα, оставляя угол φ неизменным. Отмечаем перемещения, которые получают точки приложения весов шаров. Перемещения этих точек и 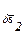направлены перпендикулярно к стержням A₁C₁ и A₂С₂ и равны

Составляем сумму работ задаваемых сил тяжести шаров на перемещениях и 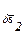, вызванных приращением угла а:

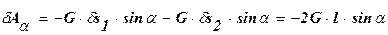
Определяем обобщенную силу по формуле (119.1): .

Для нахождения обобщенной силы 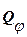, соответствующей обобщенной координате φ, сообщим углу φ приращение δφ, оставляя угол α, неизменным.

Точки приложения весов шаров при повороте регулятора на угол δφ перемещаются в плоскости, перпендикулярной к оси регулятора. Работа сил тяжести G на этих перемещениях равна нулю: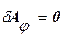

Обобщенная сила 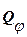, соответствующая координате φ,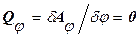

Рассмотрим механическую систему из n материальных точек, находящуюся под действием сил .

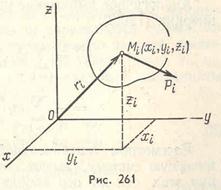
Предположим, что система имеет S степеней свободы, т. е. ее положение определяется S обобщенными координатами 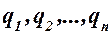. Найдем выражение обобщенной силы, соответствующей каждой обобщенной координате системы. Для этого проведем в каждую точку системы M_i из начала неподвижной системы декартовых координат радиус-вектор 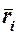(рис. 261).

При наличии нестационарных связей радиус-вектор точки так же, как и ее декартовы координаты, является функцией всех обобщенных координат и времени: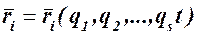

Чтобы найти обобщенную силу , соответствующую обобщенной координате сообщим координате элементарное приращение 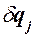тогда радиус-вектор каждой точки получит приращение, обусловленное приращением только одного аргумента :

(120.1)

Составим сумму работ всех сил, действующих на систему, на возможных перемещениях точек 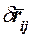, вызванных приращением координаты 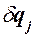. Воспользуемся для этого выражением элементарной работы силы в виде скалярного произведения (60.5):

Подставив это выражение в формулу (119.1) 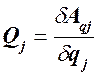получим обобщенную силу в виде суммы скалярных произведений векторов: 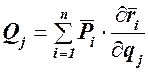(120.2)

Выразив эти скалярные произведения через проекции векторов-сомножителей на неподвижные оси декартовых координат, получим обобщенную силу - в следующем виде:

(120.3)

Аналогичное выражение можно получить и для обобщенной силы инерции: (120.4)

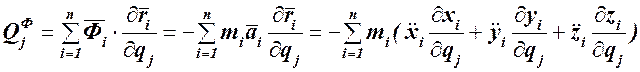
Рассмотрим теперь случай, когда силы, действующие на механическую систему, имеют потенциал. Тогда согласно(72.8) проекции этих сил на оси координат равны взятым с обратным знаком частным производным от потенциальной энергии по соответствующим координатам точек: , ,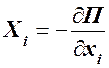

Подставим эти значения проекций сил в формулу (120.3):

(а)

Потенциальная энергия механической системы согласно (72.5) является функцией декартовых координат точек системы: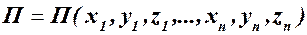

Декартовы координаты точек системы являются функциями ее обобщенных координат и времени (112.2):

, ,

Подставив в выражение (72.5) значение декартовых координат из (112.2), получим потенциальную энергию П механической системы, как функцию обобщенных координат и времени: (120.5)

В случае стационарных связей зависимость декартовых координат от обобщенных координат имеет вид (112.1):

, ,

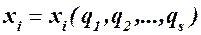Потенциальная энергия системы в этом случае является функцией только обобщенных координат: 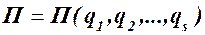(120.6)

Найдем частную производную от потенциальной энергии системы П по обобщенной координате , рассматривая П как сложную функцию обобщенных координат, определяемую зависимостями (72.5): 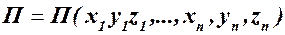и (112.1): , ,

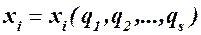Эта производная 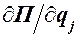определяется суммой 3n слагаемых. Каждое слагаемое равно произведению частной производной от П по одной из 3n декартовых координат точек х₁ у₂ z₁, х₂,..., z_n на производную от этой декартовой координаты по выбранной обобщенной координате .

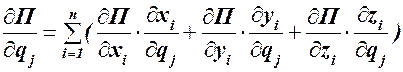(б)

Сопоставляя выражения (а) и (б), устанавливаем: (120.7)

Формулы (120.7) показывают, что в случае сил, имеющих потенциал, обобщенная сила, соответствующая обобщенной координате , равна взятой со знаком минус частной производной от потенциальной энергии механической системы по этой координате.

Вопросы для самоконтроля

1. Какая величина называется обобщенной силой, соответствующей некоторой обобщенной координате системы, и какую она имеет размерность?

2. Чему равны обобщенные реакции идеальных связей?

3. Какими формулами выражаются обобщенные силы через проекции сил
на неподвижные оси декартовых координат?

4. Как определяются обобщенные силы в случае консервативных и в случае
неконсервативных сил?

Дата добавления: 2014-01-15