Общее уравнение динамики в обобщенных силах. Условия равновесия сил

Принцип Лагранжа-Даламбера в обобщённых координатах.

Лекция IV-ОАМ-15

Преобразуем общее уравнение динамики (117.4):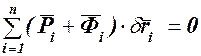

Подставим в это уравнение наиболее общие возможные перемещения точек системы 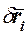, вызванные одновременными бесконечно малыми приращениями всех обобщенных координат системы. Эти перемещения равны геометрической сумме возможных перемещений, вызванных приращениями отдельных обобщенных координат, т. е.

Общее уравнение динамики примет следующий вид:

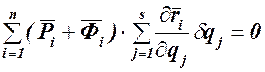(121.1)

Суммируем сначала по материальным точкам системы 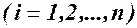, а затем по обобщенным координатам этой системы :

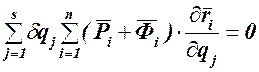
или (121.2)

Здесь 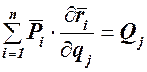обобщенная сила, соответствующая обобщенной координате .

Сумма 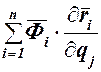является обобщенной силой инерции, соответствующей обобщенной координате : (121.3)

Пользуясь выражениями (121.2): и (121.3), получаем общее уравнение динамики (121.2) в виде (121.4)

Приращения обобщенных координат _;- произвольны и не зависят друг от друга. Поэтому в полученном уравнении все коэффициенты при этих приращениях должны быть равны нулю.

Приравняем нулю эти коэффициенты: 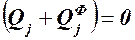(121.5)

Уравнения (121.5) эквивалентны общему уравнению динамики (121.4).

Если силы, действующие на механическую систему, уравновешиваются, т. е. механическая система находится в состоянии покоя, или все ее точки движутся прямолинейно и равномерно, то силы инерции ее точек равны нулю. Следовательно, и обобщенные силы инерции системы равны нулю:

Тогда уравнения (121.5) принимают вид 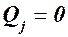(121.6)

Равенства (121.6) выражают условия равновесия сил в обобщенных силах.

[Так, например, в примере 76 (лекция IV-ОАМ-14) для рычага получено выражение обобщенной силы 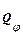, соответствующей обобщенной координате 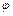. Рычаг имеет одну степень свободы. Если приложенные к нему силы уравновешиваются, то согласно (121.6) 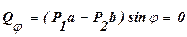т. е. сумма моментов задаваемых сил Р₁ и Р₂, действующих на рычаг, относительно опорной точки рычага равна нулю.]

Преобразуем условия равновесия (121.6) для консервативных сил, т. е. сил, имеющих потенциал.

Для любой системы сил условия равновесия имеют вид ,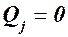

В случае консервативных сил обобщенные силы определяются формулами (120.7):

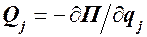
Следовательно, условия равновесия консервативной системы сил имеют вид:

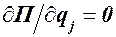
(121.7)

Вопросы для самоконтроля

1. Выведите общее уравнение динамики в обобщенных силах.

2. Какой вид имеют условия равновесия сил, приложенных к механической
системе, полученные из общего уравнения динамики в обобщенных силах?

3. Как определяются обобщенные силы в случае консервативных и в случае
неконсервативных сил?

Дата добавления: 2014-01-15