Принцип возможных перемещений в случае движения системы. Общее уравнение динамики

Принцип возможных перемещений, дающий общий метод решения задач статики, можно применить и к решению задач динамики. На основании принципа Германа-Эйлера-Даламбера для несвободной механической системы (§ 109) в любой момент времени геометрическая сумма равнодействующей задаваемых сил, равнодействующей реакций связей и силы инерции для каждой точки M_t механической системы равна нулю:

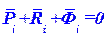
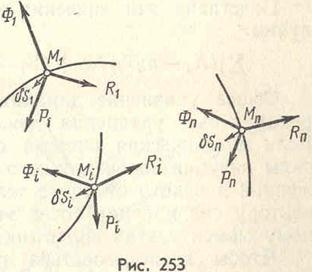Если система получает возможное перемещение, при котором каждая точка имеет возможное перемещение 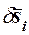, (рис. 253), то сумма работ этих сил на перемещении 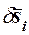, должна быть равна нулю: (117.1) 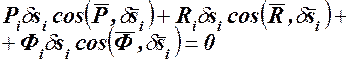Суммируем все n уравнений (117.1):

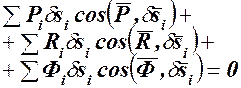(117.2) (117.2)

Положим, что все связи в рассматриваемой механической системе двусторонние и идеальные (силы трения, если они имеются, отнесены к числу задаваемых сил). Тогда сумма работ реакций связей на возможных перемещениях системы равна нулю:

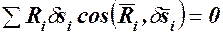
При этом условии уравнение (117.2) имеет вид

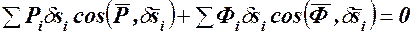(117.3)

Уравнение (117.3) называемое общим уравнением динамики, показывает, что в любой момент времени сумма работ всех задаваемых сил и сил инерции материальных точек несвободной механической системы с двусторонними идеальными связями на любом возможном ее перемещении равна нулю.

Если в каждую точку M_i системы из некоторого центра О провести вектор 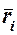, то возможное перемещение этой точки 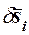, будет соответствующим приращением радиуса-вектора точки:

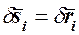(i = 2, 1,..., n).

Так как возможное перемещение точки не обязательно направлено в сторону ее действительного движения, то возможное приращение радиуса-вектора 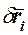не всегда равно действительному приращению радиуса-вектора точки .

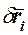Работу задаваемых сил и сил инерции 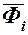на возможных перемещениях точек системы можно представить в виде скалярных произведений (60.5). Тогда уравнение (117.3) примет вид 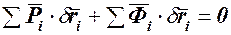или (117.4)

Обозначим Х_i, Y_i Z_i проекции задаваемых сил на неподвижные оси декартовых координат, 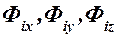- проекции сил инерции 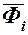, а 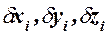- проекции векторов возможных перемещений 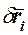на те же оси.

Пользуясь аналитическим выражением элементарной работы (60.6), уравнению (117.4) можно придать следующий вид:

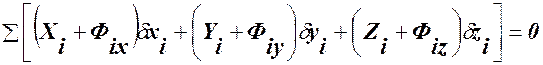(117.5)

Выразим проекции силы инерции точки на оси координат через проекции ее ускорения: , ,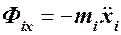

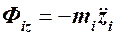
Подставив эти значения в уравнение (117.5), окончательно получим:

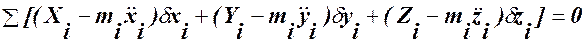(117.6)

Общее уравнение динамики (117.6) позволяет составить дифференциальные уравнения движения любой механической системы. Если механическая система состоит из отдельных твердых тел, то силы инерции точек каждого тела можно привести к силе, приложенной в некоторой точке тела, и паре сил. Сила равна главному вектору сил инерции точек этого тела, а момент пары равен главному моменту этих сил относительно центра приведения (см. § 109).

Чтобы воспользоваться принципом возможных перемещений, к каждому телу прикладывают действующие на него задаваемые силы, а также условно прикладывают силу и пару, составленные силами инерции точек тела. Затем системе сообщают возможное перемещение и для всей совокупности задаваемых сил и приведенных сил инерции составляют уравнение (117.3) или (117.6).

Если среди связей системы имеются односторонние, то для применения общего уравнения динамики необходимо, чтобы возможные перемещения системы не были освобождающими.

Вопросы для самоконтроля

1. Как формулируется принцип возможных перемещений?

2. Какие виды может иметь уравнение работ?

10. Почему принцип возможных перемещений упрощает вывод условий равновесия сил, приложенных к несвободным системам, состоящим из большого числа тел?

11. Как составляются уравнения работ для сил, действующих на механическую систему с несколькими степенями свободы?

12. Какова зависимость между движущей силой и силой сопротивления в простейших машинах?

13. Как формулируется золотое правило механики?

14. Каким образом определяют реакции связей при помощи принципа возможных перемещений?

15. Какой вид имеет общее уравнение динамики?

Дата добавления: 2014-01-15