Вопрос 3. Некоторые частные случаи движения точки

Пользуясь полученными результатами, рассмотрим некоторые частные случаи движения точки.

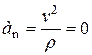1) Прямолинейное движение. Если траекторией точки является прямая линия, то . Тогда и все ускорение точки равно одному только касательному ускорению:

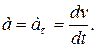
Так как в данном случае скорость изменяется только численно, то отсюда заключаем, что касательное ускорение характеризует изменение скорости по численной величине.

2) Равномерное криволинейное движение. Равномерным называется такое криволинейное движение точки, в котором численная величина скорости все время остается постоянной:

v= const. Тогда 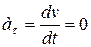и все ускорение точки равно одному только нормальному ускорению:

Вектор ускорения 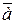направлен при этом все время по нормали к траектории точки.

Так как в данном случае ускорение появляется только за счет изменения направления скорости, то отсюда заключаем, что нормальное ускорение характеризует изменение скорости по направлению.

Найдем закон равномерного криволинейного движения. Известно, что 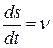или ds = v dt.

Пусть в начальный момент (t=0) точка находится от начала отсчета на расстоянии s₀. Тогда, беря от левой и правой части равенства определенные интегралы в соответствующих пределах, получим

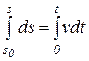или

так как v = const. Окончательно находим закон равномерного криволинейного движения точки в виде

s = s_{0 +} vt.

Если положить s₀ = 0, то s даст путь, пройденный точкой за время t. Следовательно, при равномерном движении путь, пройденный точкой, растет пропорционально времени, а скорость движения равна отношению пути ко времени

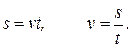
3) Равномерное прямолинейное движение. В этом случае 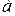_n = 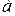_τ = 0, а значит и 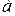=0. Заметим, что единственным движением, в котором ускорение точки все время равно нулю, является равномерное прямолинейное движение.

4) Равнопеременное криволинейное движение. Равнопеременным называется такое криволинейное движение точки, при котором касательное ускорение остается все время величиною постоянной: 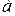= const. Найдем закон этого движения, считая, что при t=0 s=s₀, a v=v₀, где v₀ - начальная скорость точки.

Согласно формуле или dv= 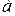_τdt

Так как 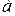_τ = const, то, беря от обеих частей последнего равенства интегралы в соответствующих пределах, получим:

v=v₀ + 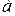_τt.

Эту формулу представим в виде

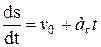или

Вторично интегрируя, найдем закон равнопеременного криволинейного движения точки в виде

Если при криволинейном движении точки модуль скорости возрастает, то движение называется ускоренным, а если убывает замедленным. Так как изменение модуля скорости характеризуется касательным ускорение, то движение будет ускоренным, если величины v и 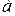, имеют одинаковые знаки (угол между векторами и 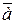острый), и замедленным, если разные (угол между и 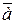тупой ).

Задача

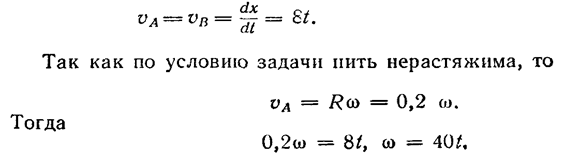
III. ЗАКЛЮЧИТЕЛЬНАЯ ЧАСТЬ (2 минуты):

Доведение общих выводов по лекции. Ответы на неясные вопросы. Задание на самоподготовку. Заполнение журнала (журналов) учебных групп.

доцент кафедры “Теоретическая механика”

кандидат технических наук, доцент

Д.Н. Миронов

Дата добавления: 2014-01-15