
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод координат Декарта. Пряма на площині
|
|
|
|
ЛЕКЦІЯ 6: АНАЛІТИЧНОЇ ГЕОМЕТРІЯ НА ПЛОЩИНІ І У ПРОСТОРІ
Нехай у декартовій прямокутній системі координат задано точки А (xA, yA) та В (xВ, yВ).
Відстань між точками А та В 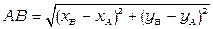 .
.
Координати точки С, яка ділить відрізок АВ у заданому відношенні 
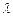 (тобто
(тобто  ):
):
 ,
, 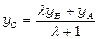 . (4.6)
. (4.6)
Зокрема, координати середини відрізка АВ – точки D:
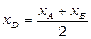 ,
, 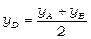 .
.
Рівняння прямої: ax + by + c =0, причому хоча б одне з чисел a, b не рівне нулеві.
Якщо 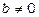 , то рівняння прямої можна звести до вигляду y = kx + m, при цьому число k називають кутовим коефіцієнтом прямої. Має місце співвідношення
, то рівняння прямої можна звести до вигляду y = kx + m, при цьому число k називають кутовим коефіцієнтом прямої. Має місце співвідношення  , де
, де 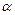 – кут між додатним напрямком вісі Ox та прямою, який відраховується у додатному напрямку (проти годинникової стрілки).
– кут між додатним напрямком вісі Ox та прямою, який відраховується у додатному напрямку (проти годинникової стрілки).
Рівняння прямої з кутовим коефіцієнтом k, яка проходить через точку M (x 0, y 0) має вигляд
y – y 0= k (x – x 0). (4.7)
Рівняння прямої, яка проходить через точки А (xA, yA) та В (xВ, yВ), має вигляд
(y – yА)(xВ – xА) = (x – xА)(yВ – yА). (4.8)
У випадку, коли пряма АВ не паралельна координатним прямим Ox або Oy, рівняння (3) можна записати у вигляді
 (4.9)
(4.9)
Якщо пряма АВ паралельна прямій Ox, то рівняння (4.8) приймає вигляд y = yА, а якщо вона паралельна прямій Oy, то рівняння (4.8) має вигляд x = xА.
Для того, щоб знайти спільні точки прямих l 1: a 1 x + b 1 y + c 1=0 та l 2: a 2 x + b 2 y + c 2=0, необхідно розв’язати систему
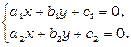 (4.10)
(4.10)
При цьому можливі три випадки:
1)  (при
(при 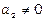 і
і  цю умову можна записати у вигляді
цю умову можна записати у вигляді 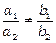 , що означає непропорційність коефіцієнтів при змінних x, y в рівняннях прямих l 1 та l 2). В цьому випадку система (4.10) має єдиний розв’язок (x 0, y 0), а прямі l 1 та l 2 перетинаються в точці (x 0, y 0);
, що означає непропорційність коефіцієнтів при змінних x, y в рівняннях прямих l 1 та l 2). В цьому випадку система (4.10) має єдиний розв’язок (x 0, y 0), а прямі l 1 та l 2 перетинаються в точці (x 0, y 0);
2)  (при
(при 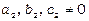 цю умову можна записати у вигляді
цю умову можна записати у вигляді  , тобто при цьому пропорційні тільки коефіцієнти при змінних x, y в рівняннях прямих l 1 та l 2). В цьому випадку система (4.10) не має розв’язків і
, тобто при цьому пропорційні тільки коефіцієнти при змінних x, y в рівняннях прямих l 1 та l 2). В цьому випадку система (4.10) не має розв’язків і  || l 2;
|| l 2;
3) 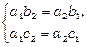 (при
(при 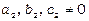 цю умову можна записати у вигляді
цю умову можна записати у вигляді  , тобто при цьому пропорційні всі коефіцієнти у рівняннях прямих l 1 та l 2). В цьому випадку система (4.10) має нескінченну кількість розв’язків, а прямі l 1 та l 2 при цьому співпадають.
, тобто при цьому пропорційні всі коефіцієнти у рівняннях прямих l 1 та l 2). В цьому випадку система (4.10) має нескінченну кількість розв’язків, а прямі l 1 та l 2 при цьому співпадають.
Розглянемо тепер прямі l 1: y = k 1 x + m 1 та l 2: y = k 2 x + m 2. Умови паралельності і перпендикулярності прямих l 1 та l 2 мають вигляд:
 || l 2
|| l 2 
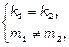


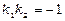 .
.
Якщо  і
і  , то гострий кут
, то гострий кут 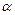 між прямими l 1 та l 2 обчислюється за формулою
між прямими l 1 та l 2 обчислюється за формулою
 , (4.11)
, (4.11)
Відстань 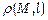 від точки M (x 0, y 0) до прямої l: ax + by + c =0 знаходиться за формулою
від точки M (x 0, y 0) до прямої l: ax + by + c =0 знаходиться за формулою
 , (4.12)
, (4.12)
зокрема, якщо пряма l має рівняння y = kx + m, формула (7) набуває вигляду
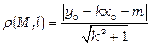 . (4.13)
. (4.13)
Відстань d (l 1, l 2) між паралельними прямими l 1: y = kx + m 1 та l 2: y = kx + m 2 знаходиться за формулою
 . (4.14)
. (4.14)
Рівняння кола радіуса R з центром в точці (x 0, y 0) має вигляд:
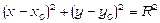 . (4.15)
. (4.15)
Приклад 5. Знайти координати точки К, яка симетрична до точки М (3;–2) відносно прямої l: y =4 x +3.
Точка К лежить на прямій l 2, яка проходить через точку М і перпендикулярна прямій l. Оскільки 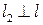 , а кутовий коефіцієнт kl прямої l дорівнює 4, то пряма l 2 має кутовий коефіцієнт
, а кутовий коефіцієнт kl прямої l дорівнює 4, то пряма l 2 має кутовий коефіцієнт 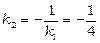 . Тоді рівняння прямої l 2 має вигляд
. Тоді рівняння прямої l 2 має вигляд 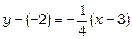

 . Тепер знаходимо координати точки N перетину прямих l та l 2, розв’язуючи систему рівнянь
. Тепер знаходимо координати точки N перетину прямих l та l 2, розв’язуючи систему рівнянь 



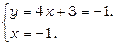
Таким чином, знайдено точку N (–1;–1). Нарешті, використовуючи формули координат середини відрізка, знаходимо координати точки К (xK, yK):



Приклад 6. Задано точки А (–4;0), В (0;3), С (0;0). Знайти рівняння бісектриси AL трикутника ABC. Знайти координати центра О кола, вписаного до трикутника ABC.
Знайдемо довжини відрізків АВ, ВС, АС так, що ВС =3, АС =4,  . За основною властивістю бісектриси AL трикутника ABC маємо:
. За основною властивістю бісектриси AL трикутника ABC маємо:  , тобто точка L ділить відрізок СВ у відношенні 4:5. Тому координати точки L знаходимо xL =0, yL =
, тобто точка L ділить відрізок СВ у відношенні 4:5. Тому координати точки L знаходимо xL =0, yL = .
.
Тепер рівняння прямої AL запишемо за формулою (4.9):


 .
.
Оскільки центр О кола, вписаного до трикутника АВС, є точкою перетину бісектрис, то його координати задовольняють систему
 де y =– x – рівняння бісектриси кута С (див. рис. 4.2). Розв’язком системи є пара (–1;–1).
де y =– x – рівняння бісектриси кута С (див. рис. 4.2). Розв’язком системи є пара (–1;–1).
Таким чином, AL:  ; O (–1;–1).
; O (–1;–1).
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 1059; Нарушение авторских прав?; Мы поможем в написании вашей работы!