Прецессионные уравнения и их анализ

;

.

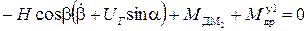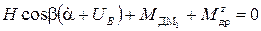Или с учетом величин моментов

; (16) 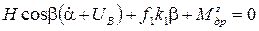. (17)

Знак f₁ и f₂ определим исходя из физических и математических соображений.

Примечание.

Сигнал с акселерометра поступает на соответствующие датчики моментов через усилители с коэффициентами усиления К_у1 и К_у2. Рассмотрим характер сигнала, снимаемого с акселерометра.

Напряжение на выходе акселерометра равно

Поэтому коэффициенты пропорциональ-ности в уравнениях (16) и (17) равны

; .

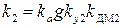Определим знаки f₁ и f₂. Углы a и b в соответствии с методом Даламбера заданы положительными. Нам необходимо с помощью датчика момента ДМ₂ создать момент, возвращающий вектор 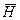в плоскость меридиана. Исходя из этого, определим знаки и 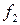математически.

Линеаризуем уравнения (16), (17) и поделим их на Н

; (18)

, (19)

где 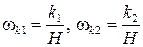- удельные скорости коррекции;

- угловые скорости дрейфа.

Запишем (18) и (19) в операторном виде и найдем характеристическое уравнение

Так как характеристическое уравнение второго порядка, то для устойчивости необходимо только выполнение условий Стодолы – положительность всех коэффициентов характеристического уравнения.

Для выполнения этого условия необходимо, чтобы и 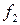соответственно равнялись

, .

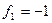При этом уравнения (18) и (19) примут вид

; (20) . (21)

Решение системы (20)-(21) будем проводить сведением к одному уравнению

Из уравнения (21) имеем:

Продифференцируем уравнение (21):

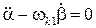, т.е.

Подставим выражения для 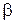и в (20):

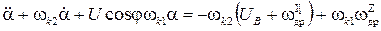(22)

САМОСТОЯТЕЛЬНО!

1). Привести уравнение (22) к виду:

.

Определить x, w₀, a_у и решить полученное уравнение при начальных условиях и, определяемым из уравнения (21) при 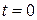, т.е.

.

2). Получить аналогичным способом уравнение для 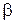и решить его.

3). Построить модели гиромаятникового и акселерометрического гирокомпасов в MatLab, Simulink и промоделировать работу.

4). Подобрать параметры, настроив компас на период М. Шулера.

Дата добавления: 2014-01-15