
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
ЛЕКЦИЯ № 4. Построение плана ускорений позволяет определить линейные ускорения точек , и , а также угловое ускорение звена 2
|
|
|
|
Построение плана ускорений позволяет определить линейные ускорения точек 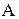 ,
, 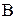 и
и 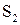 , а также угловое ускорение звена 2.
, а также угловое ускорение звена 2.
Ускорение точки  кривошипа складывается из суммы нормальной
кривошипа складывается из суммы нормальной 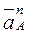 и тангенциальной
и тангенциальной 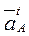 составляющих
составляющих
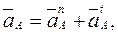 (2.42)
(2.42)
где 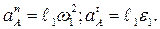
Нормальные составляющие ускорений всегда направлены по радиусу к центру вращения, а тангенциальные составляющие перпендикулярны радиусу и направлены в сторону углового ускорения.
Ускорение точки В, принадлежащей звену 2, можно представить в виде векторной суммы ускорений переносного и относительного движений
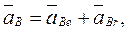 (2.43)
(2.43)
где 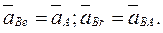
Относительное ускорение точки 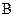 также состоит из двух составляющих
также состоит из двух составляющих
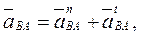 (2.44)
(2.44)
где 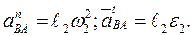
С учетом приведенных выше формул и в случае 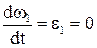 окончательно получим
окончательно получим 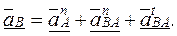 (2.45)
(2.45)
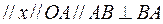
Как и раньше, одной чертой подчеркнуты векторы, известные только по направлению, а полностью известные векторы подчеркнуты двумя чертами.
Построение плана ускорений начинаем с выбора масштабного коэффициента плана ускорений 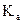 по любой известной величине – либо по
по любой известной величине – либо по 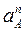 , либо по
, либо по 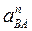 . Пусть
. Пусть
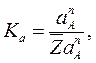 (2.46)
(2.46)
где  - длина отрезка, изображающего ускорение
- длина отрезка, изображающего ускорение 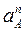 .
.
Тогда величина отрезка 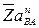 , изображающего известное ускорение
, изображающего известное ускорение 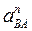 , будет
, будет
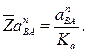
Из произвольной точки полюса плана ускорений 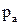 (рис. 2.9, в) откладываем отрезок
(рис. 2.9, в) откладываем отрезок  в направлении к центру вращения звена 1 – точке
в направлении к центру вращения звена 1 – точке 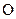 . Так как
. Так как 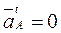 и, следовательно,
и, следовательно, 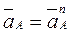 , отрезок
, отрезок 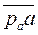 изображает полное ускорение точки
изображает полное ускорение точки  .
.
Из конца отрезка 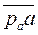 параллельно
параллельно 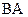 по направлению к центру относительного вращения звена 2 – точке
по направлению к центру относительного вращения звена 2 – точке  откладываем отрезок
откладываем отрезок 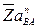 и из его конца перпендикулярно
и из его конца перпендикулярно 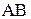 проводим линию действия тангенциальной составляющей относительного ускорения
проводим линию действия тангенциальной составляющей относительного ускорения 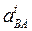 . Затем из полюса плана
. Затем из полюса плана 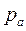 параллельно
параллельно 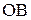 проводим линию действия абсолютного ускорения точки
проводим линию действия абсолютного ускорения точки 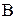 . Точка b, полученная на пересечении этих линий, определяет концы отрезков
. Точка b, полученная на пересечении этих линий, определяет концы отрезков 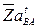 и
и 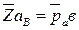 , изображающих соответствующие ускорения. Величины этих ускорений будут
, изображающих соответствующие ускорения. Величины этих ускорений будут
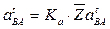 и
и 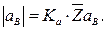
Так как вектор ускорения 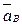 направлен в сторону отрицательной полуоси
направлен в сторону отрицательной полуоси 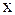 , то знак ускорения
, то знак ускорения 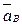 будет отрицательным.
будет отрицательным.
Соединив прямой точки 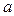 и b плана ускорений, получим отрезок
и b плана ускорений, получим отрезок 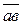 , изображающий полное относительное ускорение
, изображающий полное относительное ускорение 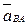 . Его величина будет
. Его величина будет
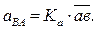
Величина углового ускорения звена 2 определяется из уравнения
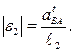 (2.47)
(2.47)
Перенеся вектор ускорения 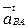 в точку
в точку 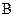 механизма и рассматривая движение точки В относительно точки
механизма и рассматривая движение точки В относительно точки  , можно определить направление ускорения
, можно определить направление ускорения 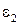 (на рис. 2.9, а ускорение
(на рис. 2.9, а ускорение 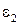 направлено по часовой стрелке и поэтому является отрицательным).
направлено по часовой стрелке и поэтому является отрицательным).
Ускорение точки 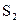 определяется из векторного уравнения
определяется из векторного уравнения
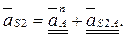 (2.48)
(2.48)
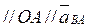
Величина относительного ускорения 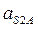 находится аналогично скорости
находится аналогично скорости 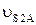 - методом пропорционального деления отрезка
- методом пропорционального деления отрезка 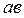 , изображающего относительное ускорение
, изображающего относительное ускорение 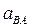
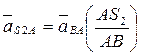 (2.49)
(2.49)
или на рис. 2.9, в
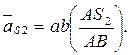
Полное ускорение точки 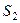 определяется как
определяется как
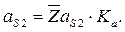
Планы скоростей и ускорений обладают следующими свойствами. Полюсы планов соответствуют неподвижным точкам механизмов (для кривошипно-ползунного механизма такой является точка 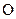 ). Из полюсов планов выходят векторы абсолютных скоростей или ускорений, а векторы относительных скоростей и ускорений располагаются вне полюсов планов.
). Из полюсов планов выходят векторы абсолютных скоростей или ускорений, а векторы относительных скоростей и ускорений располагаются вне полюсов планов.
Механизм с гидроцилиндром
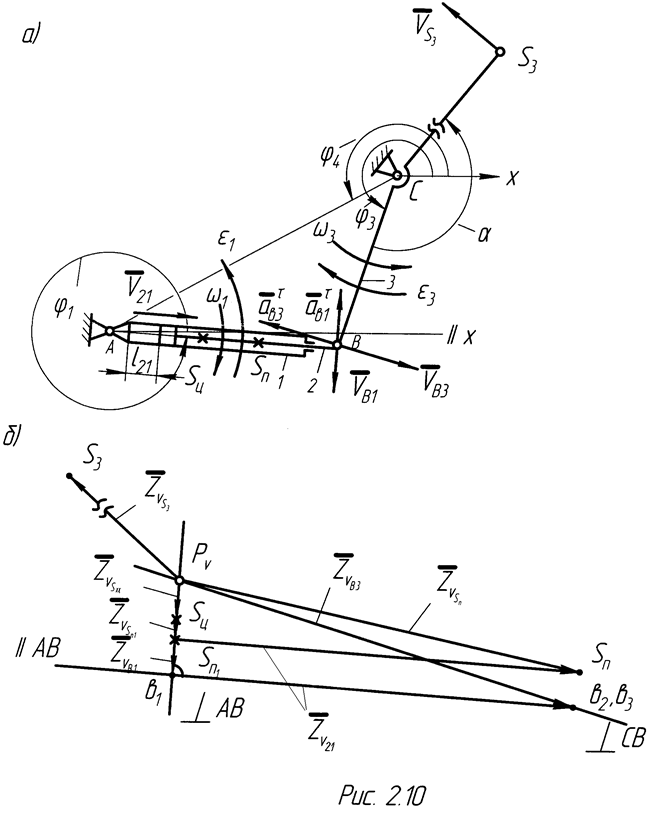
План положений механизма для заданного значения обобщенной координаты 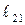 показан на рис. 2.10, а. По известным длинам звеньев
показан на рис. 2.10, а. По известным длинам звеньев 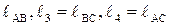 и углу
и углу 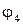 определяются угловые положения звеньев 1-2 и 3
определяются угловые положения звеньев 1-2 и 3 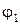 и
и 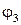 . На рисунке точка
. На рисунке точка 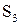 является центром тяжести звена 3, положение которого определяется углом
является центром тяжести звена 3, положение которого определяется углом 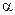 и длиной
и длиной 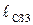 , а точки
, а точки 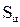 и
и 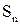 - центры тяжести соответственно цилиндра и поршня со штоком. План положений построен в соответствии с масштабным коэффициентом
- центры тяжести соответственно цилиндра и поршня со штоком. План положений построен в соответствии с масштабным коэффициентом 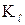 , определенным по длине какого-либо звена механизма.
, определенным по длине какого-либо звена механизма.
План скоростей позволит определить угловые скорости звеньев 1-2 и 3, линейные скорости центров тяжести всех звеньев по заданным кинематической схеме механизма, построенной в масштабе (рис. 2.10, а) и закону движения начального звена, например 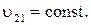
При составлении векторного уравнения для построения плана скоростей используется теорема сложения скоростей при сложном движении точки – абсолютная скорость 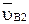 точки, принадлежащей звену 2, равна геометрической сумме переносной
точки, принадлежащей звену 2, равна геометрической сумме переносной 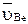 и относительной
и относительной 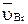 скоростей этой точки
скоростей этой точки
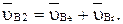 (2.50)
(2.50)
При определении переносной скорости точки предполагается, что относительное движение точки остановлено. Переносной скоростью точки 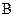 звена 2 является движение со скоростью точки
звена 2 является движение со скоростью точки 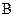 , принадлежащей звену 1
, принадлежащей звену 1 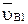 , а относительной скоростью является поступательное движение звена 2 относительно звена 1, т.е.
, а относительной скоростью является поступательное движение звена 2 относительно звена 1, т.е. 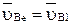 и
и 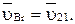
С учетом равенства 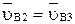 векторное уравнение скоростей будет иметь вид
векторное уравнение скоростей будет иметь вид
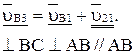 (2.51)
(2.51)
Здесь 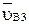 и
и 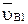 - векторы абсолютных скоростей точек
- векторы абсолютных скоростей точек 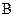 , принадлежащих соответственно звеньям 3 и 1. Они известны лишь по направлению и подчеркнуты поэтому в уравнении одной чертой;
, принадлежащих соответственно звеньям 3 и 1. Они известны лишь по направлению и подчеркнуты поэтому в уравнении одной чертой; 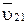 - вектор скорости поршня относительно цилиндра, известный по величине и направлению, подчеркнут двумя чертами.
- вектор скорости поршня относительно цилиндра, известный по величине и направлению, подчеркнут двумя чертами.
Данное векторное уравнение решается, поскольку оно имеет не более двух неизвестных – определению подлежат модули абсолютных скоростей точек 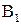 и
и 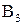
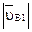 и
и 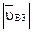 .
.
Графическое решение уравнения следует начинать с построения отрезка 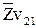 , параллельного
, параллельного 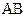 , изображающего скорость
, изображающего скорость 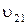 в соответствии с выбранным масштабным коэффициентом плана скоростей
в соответствии с выбранным масштабным коэффициентом плана скоростей 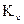 (рис. 2.10, б)
(рис. 2.10, б)
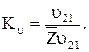 (2.52)
(2.52)
|
Далее в соответствии с уравнением (2.51) следует провести в точке начала вектора 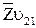 (т. b1) прямую, перпендикулярную звену
(т. b1) прямую, перпендикулярную звену 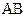 , а в точке конца вектора
, а в точке конца вектора 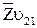 (т. b2) – прямую, перпендикулярную звену
(т. b2) – прямую, перпендикулярную звену 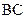 механизма. Пересечение двух прямых дает точку полюса плана скоростей
механизма. Пересечение двух прямых дает точку полюса плана скоростей 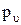 и отрезки
и отрезки 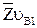 и
и 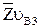 , изображающие искомые абсолютные скорости
, изображающие искомые абсолютные скорости 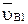 и
и 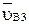 .
.
С учетом масштабного коэффициента 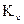 неизвестные скорости определяются как
неизвестные скорости определяются как
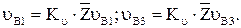
Угловые скорости звеньев 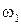 и
и 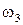 равны
равны
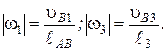 (2.53)
(2.53)
Знаки угловых скоростей определяются параллельным переносом векторов скоростей из плана скоростей в соответствующие точки механизма. Для механизма по рис. (2.10, а) 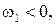 а
а 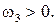
Линейная скорость центра тяжести цилиндра 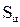 (звено 1) как точки, лежащей на звене
(звено 1) как точки, лежащей на звене 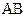 , находится методом пропорционального деления отрезка
, находится методом пропорционального деления отрезка 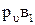 , изображающего скорость
, изображающего скорость 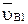 :
:
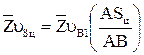 .
.
Линейная скорость центра тяжести 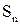 поршня, совершающего сложное движение, определяется, как и для точки
поршня, совершающего сложное движение, определяется, как и для точки 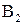 , суммированием переносной и относительной скоростей
, суммированием переносной и относительной скоростей
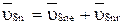
или
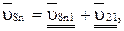 (2.54)
(2.54)
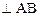
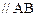
где 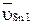 - вектор скорости точки, принадлежащей цилиндру и лежащей на расстоянии
- вектор скорости точки, принадлежащей цилиндру и лежащей на расстоянии 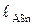 от точки
от точки  , определяется аналогично скорости точки центра тяжести цилиндра
, определяется аналогично скорости точки центра тяжести цилиндра 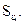
Численные значения скоростей равны
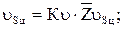
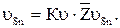
Вектор линейной скорости центра тяжести третьего звена 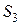 направлен перпендикулярно линии СS3 в соответствии со знаком угловой скорости
направлен перпендикулярно линии СS3 в соответствии со знаком угловой скорости 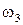 . Величина скорости определяется как
. Величина скорости определяется как 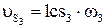 .
.
План ускорений механизма с гидроцилиндром позволяет определить угловые ускорения звеньев 1-2 и 3, а также линейные ускорения центров тяжести всех звеньев.
При составлении уравнения ускорений следует учитывать, что абсолютное ускорение 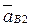 точки
точки 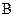 , принадлежащей второму звену, складывается из геометрической суммы трех ускорений – переносного вместе с первым звеном
, принадлежащей второму звену, складывается из геометрической суммы трех ускорений – переносного вместе с первым звеном 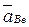 , относительного
, относительного 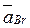 и кориолисова ускорения
и кориолисова ускорения 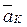 , которое появляется в том случае, если переносное движение оказывается вращательным:
, которое появляется в том случае, если переносное движение оказывается вращательным:
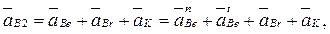 (2.55)
(2.55)
где 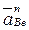 и
и 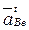 - соответственно нормальное ускорение точки В в переносном вращательном движении, направленное по радиусу вращения точки
- соответственно нормальное ускорение точки В в переносном вращательном движении, направленное по радиусу вращения точки 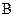 к центру вращения
к центру вращения  , и касательное ускорение, направленное перпендикулярно радиусу вращения.
, и касательное ускорение, направленное перпендикулярно радиусу вращения.
При этом
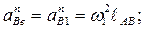
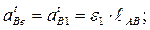
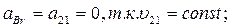
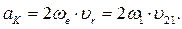
Направление кориолисова ускорения определяется поворотом в плоскости чертежа относительной скорости 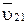 в направлении переносной угловой скорости
в направлении переносной угловой скорости 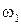 на
на 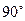 . Для положительной скорости
. Для положительной скорости 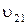 направление
направление 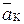 будет
будет
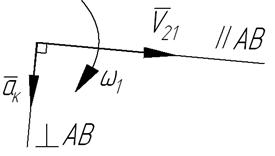
Если учесть, что
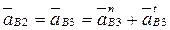 ,
,
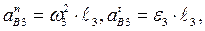
то окончательно уравнение плана ускорений будет иметь вид
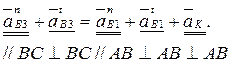 (2.56)
(2.56)
Здесь, как и в уравнении плана скоростей, векторы, известные и по величине, и по направлению, подчеркнуты двумя чертами, а векторы, для которых известно лишь направление, подчеркнуты одной чертой.
Графическое решение уравнения состоит в определении неизвестных касательных составляющих линейных ускорений 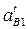 и
и 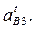
Масштабный коэффициент плана ускорений 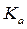 можно назначить, исходя из наибольшего известного значения ускорения. Пусть
можно назначить, исходя из наибольшего известного значения ускорения. Пусть
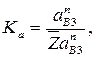 (2.57)
(2.57)
где 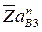 - отрезок, изображающий ускорение
- отрезок, изображающий ускорение 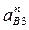 на плане ускорений.
на плане ускорений.
Тогда отрезки, пропорциональные значениям остальных известных ускорений, определятся как:
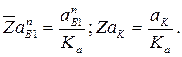
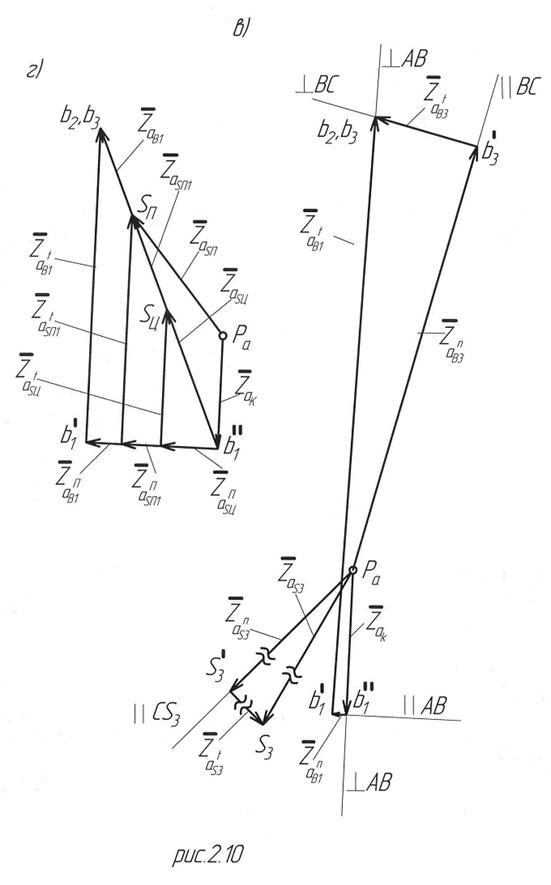
Из произвольной точки 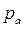 полюса плана ускорений (рис. 2.10, в) необходимо провести луч, параллельный
полюса плана ускорений (рис. 2.10, в) необходимо провести луч, параллельный 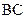 , в направлении к центру вращения
, в направлении к центру вращения 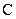 и отложить на нем отрезок
и отложить на нем отрезок 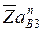 . Из конца отрезка (точка
. Из конца отрезка (точка 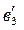 на плане) проводится прямая, перпендикулярная
на плане) проводится прямая, перпендикулярная 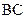 – это линия действия ускорения
– это линия действия ускорения 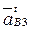 . Далее из полюса плана
. Далее из полюса плана 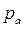 строится ускорение
строится ускорение 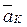 , из точки
, из точки 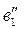 - ускорение
- ускорение 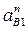 с учетом масштабного коэффициента
с учетом масштабного коэффициента 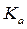 . Через точку
. Через точку 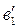 проводится линия действия ускорения
проводится линия действия ускорения 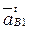 . Пересечение линий, перпендикулярных
. Пересечение линий, перпендикулярных 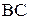 и
и 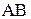 , и есть графическое решение задачи об определении касательных составляющих ускорений
, и есть графическое решение задачи об определении касательных составляющих ускорений 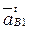 и
и 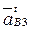 .
.
Таким образом,
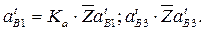
Угловые ускорения звеньев 1-2 и 3 равны
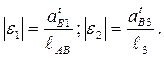 (2.58)
(2.58)
Для определения знака углового ускорения 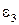 следует перенести касательную составляющую ускорения
следует перенести касательную составляющую ускорения 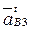 из плана ускорений в точку
из плана ускорений в точку 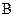 механизма. Действие ускорения по часовой стрелке определяет его отрицательный знак (рис. 2.10, а). Аналогично определяется направление ускорения
механизма. Действие ускорения по часовой стрелке определяет его отрицательный знак (рис. 2.10, а). Аналогично определяется направление ускорения 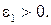
Линейное ускорение центра тяжести 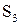 звена 3 определяется уравнением
звена 3 определяется уравнением
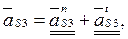 (2.59)
(2.59)
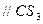
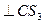
где 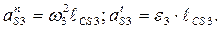
Ускорение центра тяжести 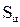 цилиндра 1 определяется методом пропорционального деления отрезка
цилиндра 1 определяется методом пропорционального деления отрезка 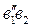 , изображающего абсолютное ускорение точки
, изображающего абсолютное ускорение точки 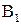 , принадлежащей цилиндру
, принадлежащей цилиндру
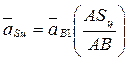 (2.60)
(2.60)
или 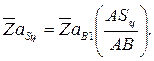
Ускорение центра тяжести 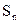 поршня со штоком определяется уравнением
поршня со штоком определяется уравнением
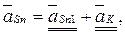 (2.61)
(2.61)
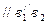
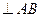
где 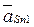 - ускорение точки цилиндра 1, располагающейся в точке
- ускорение точки цилиндра 1, располагающейся в точке 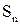 , и определяется аналогично ускорению
, и определяется аналогично ускорению 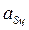
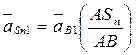 (2.62)
(2.62)
или 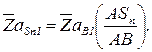
Для наглядности ускорения точек 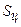 и
и 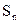 показаны на рис. 2.10, г, который является фрагментом плана ускорений и изображен не в масштабе.
показаны на рис. 2.10, г, который является фрагментом плана ускорений и изображен не в масштабе.
Действительные значения ускорений центров тяжести звеньев определяются уравнениями
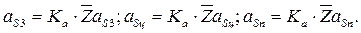
Вопросы для самоконтроля.
1. С какой целью строят план ускорений?
2. Что должно быть известно для построения плана ускорений?
3. Как определяется масштабный коэффициент плана ускорений?
4. Как определить значение и направление угловых ускорений звеньев механизма?
5. Какими свойствами обладают планы скоростей и ускорений?
6. Какие особенности имеет построение плана скоростей механизма с гидроцилиндром второго класса?
7. Что является переносным движением поршня со штоком в механизме с гидроцилиндром второго класса?
8. Что является относительным движением поршня со штоком в гидрорычажном механизме второго класса?
9. Для каких звеньев и как определяют значение и направление кориолисова ускорения?
10. Как определить величину и направление угловых скоростей и ускорений звеньев гидрорычажного механизма второго класса?
ЛЕКЦИЯ № 5
2.4. Силовой анализ рычажных механизмов
Во время движения механизма в его кинематических парах действуют силы, являющиеся силами взаимодействия между звеньями. Эти силы относятся к категории внутренних сил по отношению к механизму в целом. Знание сил в кинематических парах в дальнейшем позволит решить следующие инженерные задачи: расчет звеньев механизма на прочность, жесткость, износоустойчивость и т.п.; расчет подвижных соединений звеньев на долговечность; выбор мощности двигателя и т.д.
Задачей силового анализа рычажных механизмов является определение:
1) сил и пар сил, приложенных к механизму извне;
2) внутренних сил, действующих в кинематических парах;
3) уравновешивающей силы или уравновешивающего момента, которые надо приложить к начальному звену для обеспечения требуемого закона движения выходного звена.
Для силового анализа рычажных механизмов используют метод кинетостатики, условно приложив к каждому подвижному звену механизма главный вектор 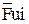 и главный момент
и главный момент 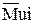 сил инерции. Тогда под действием внешних сил и моментов и инерционных сил весь механизм будет находиться в равновесии.
сил инерции. Тогда под действием внешних сил и моментов и инерционных сил весь механизм будет находиться в равновесии.
Следует отметить, что главный вектор 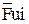 и главный момент
и главный момент 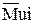 не имеют никакого физического содержания, т.е. это фиктивные силы, но с их помощью учитывается ускоренное движение звеньев.
не имеют никакого физического содержания, т.е. это фиктивные силы, но с их помощью учитывается ускоренное движение звеньев.
Для кинетостатической определимости плоский механизм не должен иметь избыточных связей. Найдём условие кинетостатической определимости плоских рычажных механизмов, которые содержат низшие вращательные и поступательные кинематические пары. Как известно из теоретической механики, сила взаимодействия двух соприкасающихся тел при отсутствии трения направлена по общей нормали к их поверхности.
Во вращательной паре сила, действующая на звено 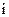 со стороны звена
со стороны звена 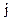
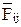 направлена нормально к цилиндрической поверхности соприкосновения обоих звеньев, т.е. проходит через центр шарнира
направлена нормально к цилиндрической поверхности соприкосновения обоих звеньев, т.е. проходит через центр шарнира  (рис. 2.11, а). Модуль силы
(рис. 2.11, а). Модуль силы 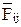 и угол
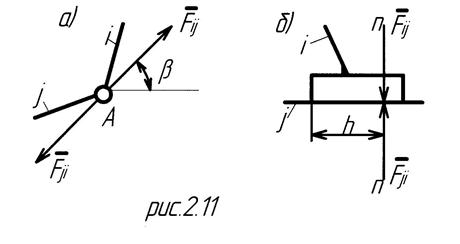
и угол 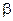 неизвестны. Эта пара приносит в расчет две неизвестные величины.
неизвестны. Эта пара приносит в расчет две неизвестные величины.
В поступательной паре сила 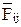 направлена по нормали
направлена по нормали 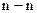 к поверхности соприкосновения звеньев (рис. 2.11, б). Модуль силы
к поверхности соприкосновения звеньев (рис. 2.11, б). Модуль силы 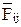 и плечо
и плечо  неизвестны. И эта низшая пара приносит в расчет две неизвестные величины.
неизвестны. И эта низшая пара приносит в расчет две неизвестные величины.
Все сказанное о силах 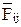 относится к силам
относится к силам 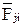 , приложенным к звену
, приложенным к звену 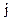 от звена
от звена 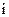 , т.к. силы взаимодействия
, т.к. силы взаимодействия 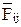 и
и 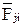 связаны третьим законом Ньютона:
связаны третьим законом Ньютона: 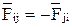 .
.
Если плоская кинематическая цепь содержит 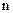 подвижных звеньев и
подвижных звеньев и 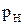 низших кинематических пар, то для нее суммарное количество неизвестных величин в кинематических парах равно
низших кинематических пар, то для нее суммарное количество неизвестных величин в кинематических парах равно 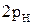 , а количество уравнений равновесия равно
, а количество уравнений равновесия равно 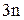 , т.к. для каждого звена можно составить 3 уравнения кинетостатики:
, т.к. для каждого звена можно составить 3 уравнения кинетостатики: 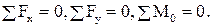
Для кинетостатической определимости такой цепи необходимо выполнение условия 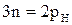 или
или 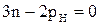 . Сопоставив это выражение с выражением (2.1), полученным для плоской структурной группы любого класса с низшими парами, можно сделать вывод, что любая структурная группа, сколь бы сложной она ни была, является статически определимой.
. Сопоставив это выражение с выражением (2.1), полученным для плоской структурной группы любого класса с низшими парами, можно сделать вывод, что любая структурная группа, сколь бы сложной она ни была, является статически определимой.
Для плоского механизма без избыточных связей 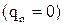 с одними низшими парами
с одними низшими парами 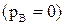 формула Чебышева имеет вид
формула Чебышева имеет вид 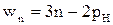 или
или 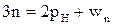 . Оставшиеся
. Оставшиеся 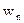 уравнений используются для определения уравновешивающих сил или уравновешивающих моментов, приложенных к начальным звеньям. Если
уравнений используются для определения уравновешивающих сил или уравновешивающих моментов, приложенных к начальным звеньям. Если 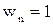 и начальное звено совершает поступательное движение, то определяют одну уравновешивающую силу
и начальное звено совершает поступательное движение, то определяют одну уравновешивающую силу 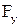 , при вращательном движении начального звена определяют уравновешивающий момент
, при вращательном движении начального звена определяют уравновешивающий момент 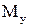 .
.
На основании вышеизложенного общая методика силового анализа рычажных механизмов без избыточных связей такова: силовой анализ ведется погруппно, начиная от группы, наиболее удаленной от первичного механизма, и заканчивая расчетом самого первичного механизма. Таким образом, силовой расчет проводится в порядке, обратном кинематическому.
При наличии избыточных связей в механизме 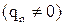 метод кинетостатики не пригоден, необходимо использовать методы теории упругости.
метод кинетостатики не пригоден, необходимо использовать методы теории упругости.
Существуют два метода силового анализа рычажных механизмов: аналитический и графический. Каждый из них обладает теми же достоинствами и недостатками, указанными в разделе кинематического анализа механизмов.
Независимо от метода расчета исходными данными являются:
1) кинематическая схема;
2) массы и моменты инерции звеньев, положения центров масс звеньев;
3) закон движения механизма;
4) внешнее силовое нагружение.
Внешнее силовое нагружение может быть представлено следующей группой сил и моментов.
1. Массовые внешние силы: силы тяжести 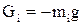 ; силы инерции внешние, связанные с движением объекта, на котором находится механизм,
; силы инерции внешние, связанные с движением объекта, на котором находится механизм, 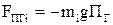 ,
, 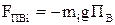 , где
, где 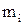 - масса
- масса 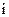 - того звена,
- того звена, 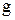 – ускорение свободного падения,
– ускорение свободного падения, 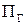 и
и 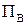 - горизонтальная и вертикальная перегрузки, равные отношению соответственно горизонтальной
- горизонтальная и вертикальная перегрузки, равные отношению соответственно горизонтальной 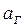 или вертикальной
или вертикальной 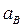 составляющей ускорения и величины
составляющей ускорения и величины 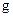 :
: 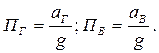 Работа этих сил за цикл равна нулю.
Работа этих сил за цикл равна нулю.
2. Массовые внутренние силы – это главный вектор сил инерции и главный момент сил инерции звена 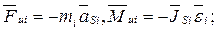 где
где 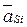 - линейное ускорение центра масс звена,
- линейное ускорение центра масс звена, 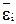 - угловое ускорение звена,
- угловое ускорение звена, 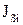 - момент инерции
- момент инерции 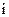 - того звена относительно оси, проходящей через центр масс звена перпендикулярно плоскости его движения. Работа этих сил за цикл также равна нулю.
- того звена относительно оси, проходящей через центр масс звена перпендикулярно плоскости его движения. Работа этих сил за цикл также равна нулю.
7. Силы полезного сопротивления – это силы, для преодоления которых предназначен механизм. Ими могут быть силы резания, давления, сжатия и другие технологические силовые факторы. Работа за цикл этих сил – отрицательная величина.
8. Силы вредного сопротивления – это внешние и внутренние силы трения. Внешние силы трения возникают в исполнительном устройстве, приводимом в действие механизмом. Внутренние силы трения возникают в кинематических парах. Работа за цикл этих сил также отрицательна.
9. Движущие силы и моменты – это уравновешивающая сила 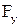 или уравновешивающий момент
или уравновешивающий момент 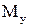 , которые должны быть приложены к начальному звену со стороны двигателя. Эти силы за цикл совершают положительную работу.
, которые должны быть приложены к начальному звену со стороны двигателя. Эти силы за цикл совершают положительную работу.
2.4.1. Аналитический метод силового анализа механизмов
Аналитический метод рассмотрим на примере двух механизмов.
Кривошипно-ползунный механизм.
Исходными данными являются: 1) кинематическая схема (рис. 2.5, а);
2) массы звеньев 2 и 3; причем, центр масс звена 3 располагается в точке 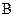 , т.е.
, т.е. 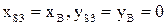 т.к. механизм центральный; масса звена 1, как правило, пренебрежимо мала; 3) момент инерции звена 2; 4) величина горизонтальной перегрузки; 5) постоянная сила трения в уплотнениях при движении поршня 3
т.к. механизм центральный; масса звена 1, как правило, пренебрежимо мала; 3) момент инерции звена 2; 4) величина горизонтальной перегрузки; 5) постоянная сила трения в уплотнениях при движении поршня 3 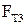 ; 6) сила сопротивления
; 6) сила сопротивления 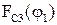 , действующая на поршень, заданная в табличной форме.
, действующая на поршень, заданная в табличной форме.
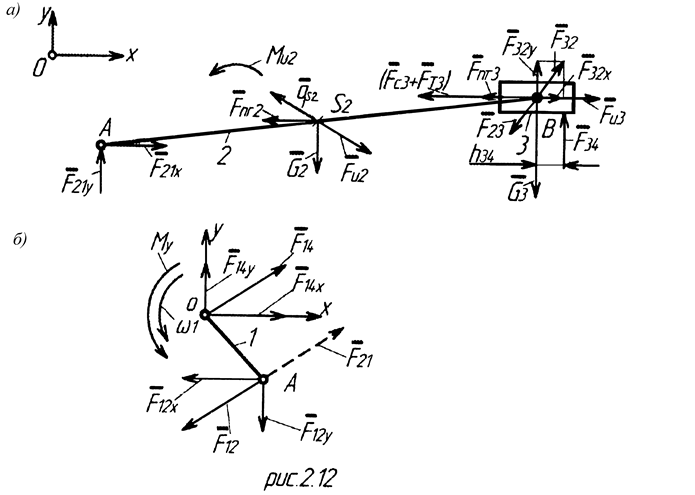
Силовой анализ следует начать со структурной группы, состоящей из звеньев 2, 3. Силовое нагружение группы представлено на рис. 2.12, а. Неизвестные силы во вращательных кинематических парах разложим на составляющие по осям координат 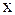 и
и 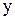 . Неизвестными являются силы
. Неизвестными являются силы 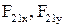 , сила
, сила 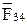 и ее плечо
и ее плечо 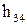 , а также модуль и направление сил взаимодействия в шарнире
, а также модуль и направление сил взаимодействия в шарнире 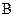 , связанных соотношением
, связанных соотношением 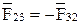 .
.
Для определения шести неизвестных необходимо составить шесть уравнений равновесия.
1. Сумма проекций на ось 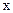 сил, приложенных к звеньям 2 и 3, равна нулю
сил, приложенных к звеньям 2 и 3, равна нулю 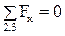 . Следовательно,
. Следовательно,
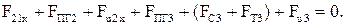 (2.63)
(2.63)
Из уравнения (2.63) определяется сила 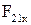 . Знаки в этом уравнении, как и во всех последующих, имеют алгебраический смысл. Это значит, что числовые значения известных проекций сил подставляются в уравнения равновесия со строгим соблюдением их знаков.
. Знаки в этом уравнении, как и во всех последующих, имеют алгебраический смысл. Это значит, что числовые значения известных проекций сил подставляются в уравнения равновесия со строгим соблюдением их знаков.
2. Сумма моментов всех сил, действующих на звено 2 и взятых относительно точки 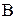 , равна нулю
, равна нулю 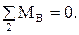 Или
Или 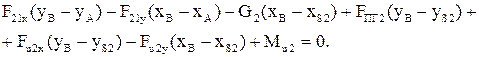 (2.64)
(2.64)
Здесь координаты точек 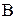 и
и 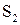 известны из кинематического анализа механизма (раздел 2.3.1); координаты точки
известны из кинематического анализа механизма (раздел 2.3.1); координаты точки  определяются формулами
определяются формулами 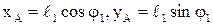 (рис. 2.5, а); проекции силы инерции звена 2 равны
(рис. 2.5, а); проекции силы инерции звена 2 равны 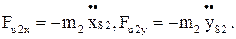 Из уравнения (2.64) определяется сила
Из уравнения (2.64) определяется сила 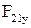 .
.
3. Сумма проекций на ось 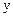 сил, приложенных к звеньям 2 и 3, равна нулю
сил, приложенных к звеньям 2 и 3, равна нулю 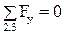 . Следовательно,
. Следовательно,
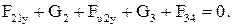 (2.65)
(2.65)
Отсюда определяется сила 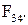
4. Сумма моментов сил, действующих на звено 3, взятых относительно точки 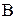 , равна нулю
, равна нулю 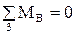 . Так как все силы, приложенные к звену 3, проходят через точку
. Так как все силы, приложенные к звену 3, проходят через точку 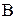 , то и сила
, то и сила 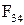 также проходит через точку
также проходит через точку 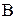 , т.е. плечо
, т.е. плечо 
5. Сумма проекций всех сил, приложенных к звену 3, на ось 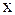 равна нулю
равна нулю 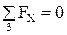 :
:
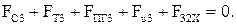 (2.66)
(2.66)
Отсюда определяется сила 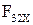 .
.
6. Сумма проекций на ось 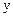 всех сил звена 3 равна нулю
всех сил звена 3 равна нулю 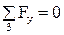 :
:
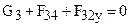 . (2.67)
. (2.67)
Из этого уравнения определяется сила 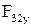 .
.
Два последних уравнения могли быть составлены для звена 2. Тогда они позволили бы определить силы 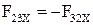 и
и 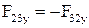 .
.
Модуль силы во вращательной кинематической паре, например 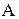 , определяется формулой
, определяется формулой
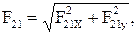 (2.68)
(2.68)
а направление силы определяется углом 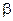 (рис. 2.11, а)
(рис. 2.11, а)
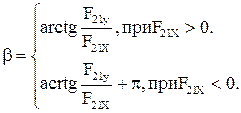 (2.69)
(2.69)
Для определения силы 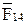 в кинематической паре
в кинематической паре 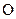 и уравновешивающего момента
и уравновешивающего момента 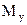 необходимо рассмотреть равновесие начального звена (рис. 2.12, б). На это звено действует лишь известная сила во вращательной кинематической паре
необходимо рассмотреть равновесие начального звена (рис. 2.12, б). На это звено действует лишь известная сила во вращательной кинематической паре 
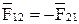 . Величина уравновешивающего момента определяется из уравнения равновесия звена 1 в виде суммы моментов сил, взятых относительно точки
. Величина уравновешивающего момента определяется из уравнения равновесия звена 1 в виде суммы моментов сил, взятых относительно точки 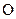
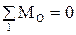 . Или
. Или
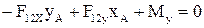 . (2.70)
. (2.70)
Очевидно, что 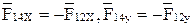 .
.
Результаты силового анализа, выполненного по приведенному алгоритму на ЭВМ, позволяют получить силовые характеристики механизма.
Примеры таких характеристик показаны на рис. 2.13. Характеристики получены для силы сопротивления 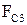 , которая равна нулю для холостого хода ползуна
, которая равна нулю для холостого хода ползуна 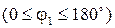 и изменяется по параболической зависимости для рабочего хода
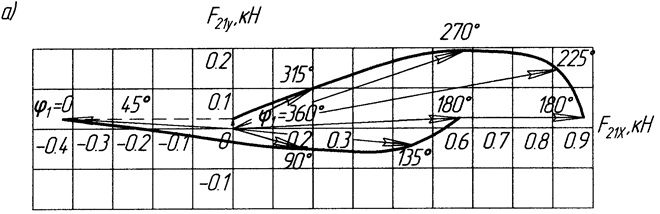
и изменяется по параболической зависимости для рабочего хода 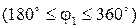 . На рис. 2.13, а показан годограф силы
. На рис. 2.13, а показан годограф силы 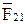 , действующей в кинематической паре А на звено 2. Годограф силы показывает изменение величины и направления вектора силы в зависимости от обобщенной координаты (в нашем примере
, действующей в кинематической паре А на звено 2. Годограф силы показывает изменение величины и направления вектора силы в зависимости от обобщенной координаты (в нашем примере 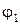 ). При построении годографа силы масштабы вертикальной и горизонтальной составляющих этой силы должны быть одинаковыми, и отсчет двух составляющих должен идти от нулевого значения. В противном случае действительное направление вектора силы будет потеряно. На годографе силы
). При построении годографа силы масштабы вертикальной и горизонтальной составляющих этой силы должны быть одинаковыми, и отсчет двух составляющих должен идти от нулевого значения. В противном случае действительное направление вектора силы будет потеряно. На годографе силы 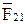 для углов
для углов 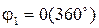 и
и 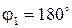 наблюдаются скачки силы. Они связаны со скачкообразным изменением сил трения
наблюдаются скачки силы. Они связаны со скачкообразным изменением сил трения 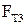 и сопротивления
и сопротивления 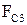 при изменении направления движения ползуна.
при изменении направления движения ползуна.
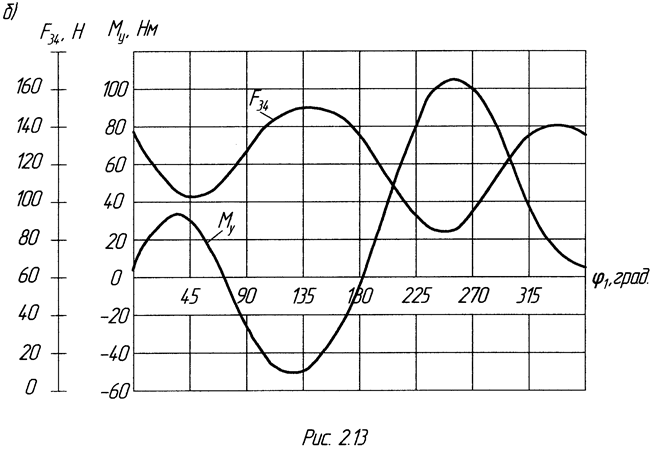
На рис. 2.13, б представлены зависимости уравновешивающего момента 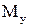 и силы
и силы 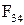 от обобщенной координаты
от обобщенной координаты 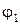 .
.
Механизм с гидроцилиндром.
Известны кинематическая схема (рис. 2.10, а); массы и моменты инерции звеньев; величина горизонтальной перегрузки 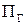 ; постоянная величина момента трения в шарнире
; постоянная величина момента трения в шарнире 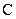
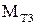 ; сила сопротивления
; сила сопротивления 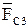 , действующая на звено 3 в точке
, действующая на звено 3 в точке 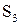 , заданная в табличной форме; постоянная сила трения в гидроцилиндре
, заданная в табличной форме; постоянная сила трения в гидроцилиндре 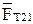 . Необходимо определить силы во вращательных кинематических парах
. Необходимо определить силы во вращательных кинематических парах 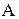 ,
, 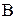 и С, силу в поступательной кинематической паре, образованной цилиндром 1 и поршнем со штоком 2, а также уравновешивающую силу
и С, силу в поступательной кинематической паре, образованной цилиндром 1 и поршнем со штоком 2, а также уравновешивающую силу 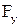 , которую надо приложить со стороны жидкости к поршню цилиндра, чтобы весь механизм находился в равновесии.
, которую надо приложить со стороны жидкости к поршню цилиндра, чтобы весь механизм находился в равновесии.
Поскольку механизм с гидроцилиндром является неделимой структурной единицей, силовой анализ проводится для всего механизма. Расчет состоит из двух этапов. На первом этапе расчета определяют силы в шарнирах А, В и С, мысленно “замораживая” поршень со штоком в гидроцилиндре в расчетном положении. Таким образом, механизм рассматривается как двухповодковая группа первого вида.
На втором этапе, отделив звено 1 от звена 2, определяют остальные неизвестные силы.
Схема механизма с “замороженным” гидроцилиндром со всеми действующими на него силами и моментами представлена на рис. 2.14, а. На рисунке не показаны силы инерции и моменты инерции звеньев, которыми можно пренебречь ввиду их малости.
Запишем шесть уравнений равновесия, из которых можно определить неизвестные силы, действующие во вращательных парах А, В и С.
1)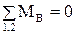 . Или
. Или
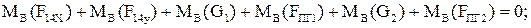 (2.71)
(2.71)
2)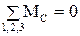 . Или
. Или
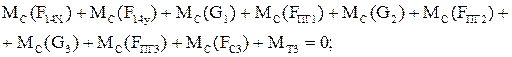 (2.72)
(2.72)
Совместное решение уравнений даст значения неизвестных сил 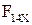 и
и 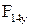 .
.
Знаки в уравнениях моментов поставлены формально, а моменты сил определяются как в примере кривошипно-ползунного механизма.
3)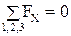 . Или
. Или
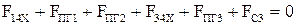 , (2.73)
, (2.73)
откуда определяется сила 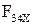 .
.
4)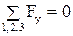 . Или
. Или
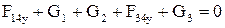 , (2.74)
, (2.74)
откуда определяется сила 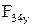 .
.
5)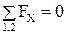 . Или
. Или
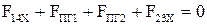 , (2.75)
, (2.75)
отсюда определяется сила 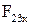
6)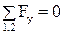 . Или
. Или
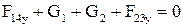 , (2.76)
, (2.76)
отсюда определяется сила 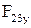 .
.
Для определения уравновешивающей силы 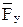 и силы, действующей в поступательной паре звеньев 1 и 2, отделим поршень со штоком от цилиндра и рассмотрим равновесие начального звена 2 (рис. 2.14, б). Поступательная пара образована двумя точками контакта цилиндра и поршня со штоком
и силы, действующей в поступательной паре звеньев 1 и 2, отделим поршень со штоком от цилиндра и рассмотрим равновесие начального звена 2 (рис. 2.14, б). Поступательная пара образована двумя точками контакта цилиндра и поршня со штоком 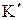 и
и 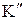 , в которых действуют силы
, в которых действуют силы 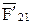 и
и 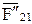 .
.
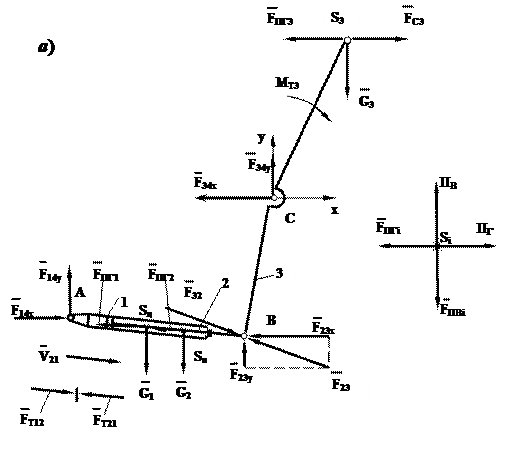
б) 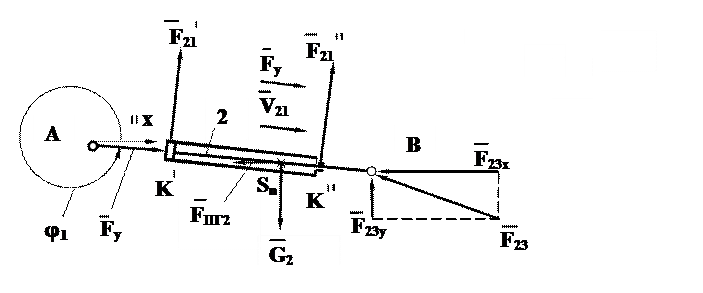
Рис. 2.14
Для определения трех неизвестных сил можно составить три уравнения равновесия
1)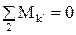 . Или
. Или
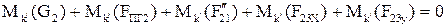 ; (2.77)
; (2.77)
2)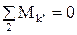 . Или
. Или
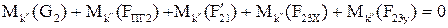 ; (2.78)
; (2.78)
3) Сумма всех сил, действующих на звено 2, в проекции на линию 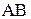 равна нулю
равна нулю
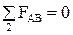 . Или
. Или
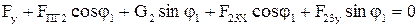 . (2.79)
. (2.79)
Из трех уравнений определяются соответственно силы 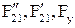 .
.
Приведенный алгоритм позволяет получить с помощью ЭВМ силовые характеристики механизма с гидроцилиндром. В качестве примера на
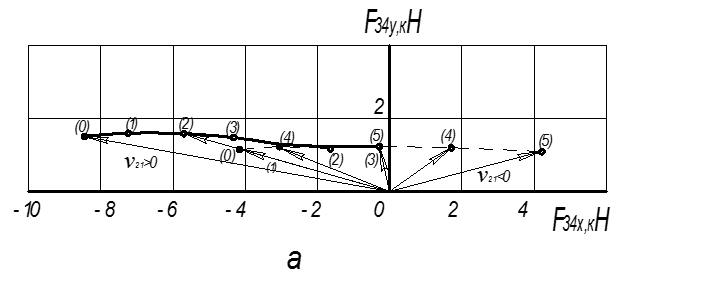
рис. 2.15,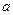 приведен годограф силы в шарнире
приведен годограф силы в шарнире 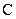
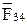 . Сплошной линией обозначен годограф, соответствующий положительной скорости поршня, а штриховой – отрицательной. Номера точек (0)…(5) указывают пять дискретных положений поршня в цилиндре при изменении обобщенной координаты от
. Сплошной линией обозначен годограф, соответствующий положительной скорости поршня, а штриховой – отрицательной. Номера точек (0)…(5) указывают пять дискретных положений поршня в цилиндре при изменении обобщенной координаты от 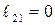 до
до 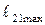 .
.
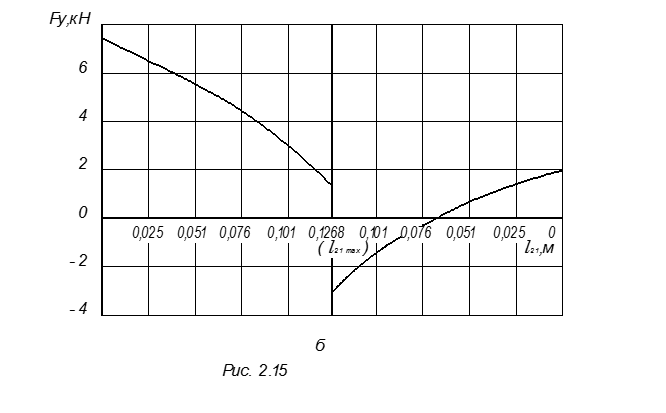
На рис. 2.15,б показана зависимость уравновешивающей силы 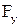 от положения поршня для двух направлений движения поршня в цилиндре. В двух точках, соответствующих двум крайним положениям поршням в цилиндре, на годографе силы и на зависимости
от положения поршня для двух направлений движения поршня в цилиндре. В двух точках, соответствующих двум крайним положениям поршням в цилиндре, на годографе силы и на зависимости 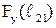 наблюдаются скачки. Они связаны со скачкообразным изменением силы трения
наблюдаются скачки. Они связаны со скачкообразным изменением силы трения 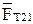 и момента трения
и момента трения 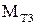 .
.
|
|
|
|
Вопросы для самоконтроля.
1. Каковы задачи силового анализа рычажных механизмов?
2. Что называют уравновешивающей силой и уравновешивающим моментом?
3. В чём заключается метод кинетостатики?
4. Как действуют силы взаимодействия в низших вращательных и поступательных кинематических парах?
5. Что является статически определимой системой плоских рычажных механизмов, содержащих только низшие кинематические пары?
6. Каков порядок проведения силового анализа рычажных механизмов без избыточных связей при отсутствии трения в кинематических парах?
7. Какие исходные данные необходимы для проведения силового анализа рычажных механизмов?
8. Какими силами и моментами представлено внешнее силовое нагружение рычажного механизма?
9. Какие методы используют для силового анализа рычажных механизмов и каковы особенности их использования?
10. Что показывает годограф силы в кинематической паре?
11. Какова особенность проведения силового анализа механизмов с гидроцилиндром?
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 2080; Нарушение авторских прав?; Мы поможем в написании вашей работы!