
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Прямая на плоскости и кривые второго порядка
|
|
|
|
1. Даны вершины  треугольника
треугольника 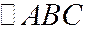 .
.
Найдите:
А) уравнение стороны 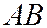 :
:
Находится по формуле: 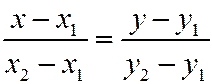 .
.
Б) уравнение высоты 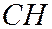 :
:
1. Написать уравнение прямой 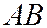 , проходящей через точки
, проходящей через точки  и
и 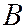 , по формуле:
, по формуле: 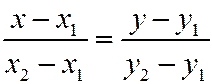 .
.
2. Записать полученное уравнение в виде: 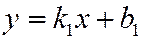 .
.
3. Использовать условие перпендикулярности двух прямых и найти угловой коэффициент прямой: 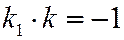 или
или 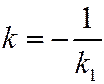 .
.
4. Написать уравнение прямой:  .
.
В) уравнение медианы  :
:
1.Определить координаты точки  середины вектора
середины вектора
 :
: .
.
2. Написать уравнение прямой, проходящей через точку  и
и  , по формуле:
, по формуле: 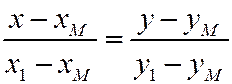 .
.
Г) точку 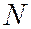 пересечения медианы
пересечения медианы 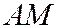 и высоты
и высоты 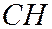 :
:
Решить систему уравнений, составленных из уравнений прямых 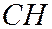 и
и 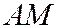
(см. п. Б и В).
Д) уравнение прямой, проходящей через вершину 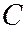 параллельно стороне
параллельно стороне 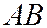 :
:
1. Записать уравнение прямой 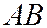 (см. п.А).
(см. п.А).
2. Записать его в виде  .
.
3. Использовать условие параллельности двух прямых и найти угловой коэффициент прямой, параллельной прямой 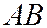 :
: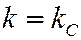 .
.
4. Написать уравнение искомой прямой, проходящей через точку 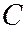 :
: 
Е) расстояние от точки 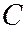 до прямой
до прямой 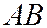 :
:
1. Выписать совместно уравнения прямых: 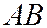 и
и 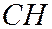 .
.
2. Найти решение полученной системы уравнений 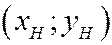 . Это координаты точки
. Это координаты точки 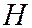 пересечения прямой
пересечения прямой 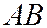 и
и 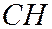 .
.
3. Найти длину отрезка 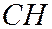 по формуле:
по формуле:  .
.
Алгоритм определения типа кривой второго порядка по заданному общему уравнению (выписать ее основные параметры).
1. Ознакомиться с каноническими уравнениями кривых второго порядка.
2. Выделить полные квадраты независимых переменных (используя формулы  ).
).
3. Преобразовать уравнение к одному из следующих видов:
1) 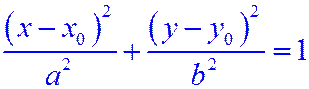 - эллипс;
- эллипс;
2)  - гипербола;
- гипербола;
с) парабола:

4. Определить тип кривой, если уравнение привели к виду:
а) – эллипс; б) – гипербола; с) – парабола.
5. Выписать параметры кривой из ее уравнения.
Для эллипса и гиперболы:
а) полуоси 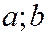 ;
;
б) расстояние между фокусами 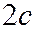 , где
, где 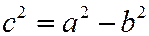 - для эллипса (если
- для эллипса (если 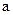 - большая полуось) и
- большая полуось) и  (для гиперболы);
(для гиперболы);
с) координаты 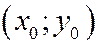 центра симметрии.
центра симметрии.
Для параболы:
а) координаты вершины 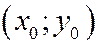 ;
;
б) координаты фокуса: 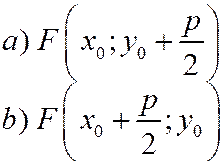 .
.
Сравнительная таблица основных свойств, для кривых второго порядка
| Кривая | Эллипс | Гипербола | Парабола |
| Каноническое уравнение | 
| 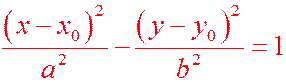
| 
|
| Параметры | 
 - большая полуось; - большая полуось;
 -малая полуось. -малая полуось.
| 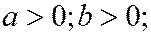
 - действительная полуось; - действительная полуось;
 -мнимая полуось. -мнимая полуось.
| 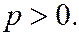 Параметр
параболы
Параметр
параболы
|
| Фокусы | 
| 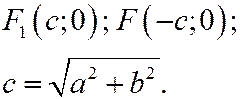
| 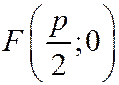
|
| Эксцентри-ситет | 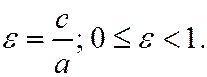
| 
| 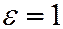
|
| Фокальные радиусы | 
| 
| 
|
| Директрисы | 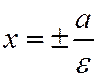
| 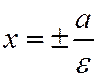
| 
|
| Расстояние от точки кривой до директрисы | 
| 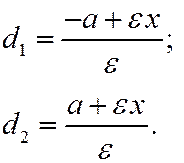
| 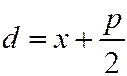
|
| Свойства директрисы | 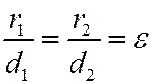
| 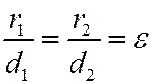
| 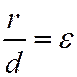
|
| Асимптоты | - | 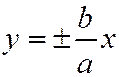
| - |
Касательная к кривой в точке 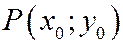
|
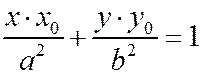
|

| 
|
|
|
|
|
|
Дата добавления: 2014-01-15; Просмотров: 749; Нарушение авторских прав?; Мы поможем в написании вашей работы!