Intersection([_|T],S2,S) :- intersection(T,S2,S)

Member(H,S2),!, intersection(T1,S2,T).

Intersection([],_,[]).

intersection([H|T1],S2,[H|T]):-

Якщо перетнути множину [1,2,3,4] з множиною [3,4,5], то результатом буде множина [3,4].

Різниця двох множин — це множина, утворена з тих елементів першої множини, що не належать другій. Різниця множин A і B позначається A-B чи A\B. Математичний смисл виглядає так: A\B={x | xÎA & хÏB}.

На малюнках різниця множин A і B (B і A) позначена штрихуванням.

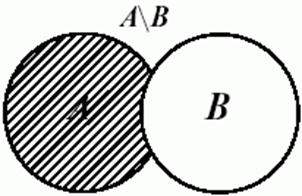
Рис. 3. Різниця множин A і B

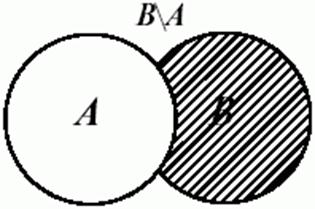
Рис. 4. Різниця множин В і А

У цій операції, на відміну від двох попередніх, важливий порядок множин. Якщо в об'єднанні чи перетині множин поміняти перший і другий аргументи місцями, результат не зміниться, тоді як

при A={1,2,3,4}, B={3,4,5}, A\B={1,2}, але B\A={5}. Тобто це відношення некоммутативне.

У предиката, що реалізує різницю, як і в об'єднання й перетину, буде три аргументи: перший — множина, з якої потрібно відняти, другий — множина, яку потрібно відняти, третій — результат вирахування з першого аргументу другого. Третій аргумент набуває ті елементи першої множини, які не належать другій множині.

Б азис рекурсії: очевидний факт, що при вирахуванні довільної множини з порожньої нічого не може бути, окрім порожньої множини.

Крок рекурсії залежить від того, чи належить перший елемент множини, з якої віднімають, множині, яку віднімають:

§ коли голова першої множини є елементом другої множини, різницею множин є різниця між хвостом першої множини та другою множиною;

§ коли голова першої множини не є елементом другої множини, різницею множин буде множина, утворена приписуванням голови першої множини до різниці між хвостом першої множини та другою множиною.

minus([],_,[]). minus([H|T],S2,S):- member(H,S2),!, minus(T,S2,S). minus([H|T],S2,[H|S]):- minus(T,S2,S).

Перетин через різницю. З математики відома тотожність AÇB = A\(A\B). Перевіримо її, записавши відповідний предикат, що реалізує перетин множин, через узяття різниці.

intersection2(A,B,S):- minus(A,B,A_B), /*A_B=A\B */ minus(A,A_B,S). /* S = A\A_B = A\(A\B) */

Емпірична перевірка свідчить, що цей предикат, так само, як і раніше визначений предикат intersection, повертає саме ті результати, які очікуються.

Відношення підмножини. Одна множина є підмножиною іншої, якщо кожен елемент першої множини належить другій множині. Факт, що множина A є підмножиною множини B, позначається через A⊆B та у теорії множин визначається так:

A ⊆ B«"x(xÎA ®xÎB).

Предикат, що реалізує це відношення, має два аргументи, обоє вхідні. Перший аргумент – множина, що розуміється як підмножина, другий – як надмножина.

Б азис рекурсії: очевидний факт, що порожня множина є підмножиною будь-якої множини.

Крок рекурсії: щоб одна множина була підмножиною іншої, достатньо, щоб її перший елемент належав другій множині (цю перевірку виконує предикат member), а її хвіст був підмножиною другої множини.

Дата добавления: 2014-01-11