Subset(A,B), not(equal(A,B))

Equal(A,B):– subset(A,B), subset(B,A).

Subseti(A,B):- intersection(A,B,A).

Subsetu(A,B):- union(A,B,B).

Subset([H|T],S):– member(H,S), subset(T,S).

Subset([],_).

Це відношення можна також визначити через уже визначені предикати union і intersection.

З математики відомо, що

A ⊆ B«AÈB=B.

Тобто, одна множина є підмножиною іншої тоді й тільки тоді, коли їх об'єднання співпадає із другою множиною.

Або, аналогічно,

A ⊆ B«AÇB=А.

Тобто одна множина є підмножиною іншої тоді й тільки тоді, коли їхній перетин збігається з першою множиною.

Обидва ці математичні співвідношення на Прологу мають вигляд:

Перевірка на прикладах показує, що предикати subset, subsetu, subseti дають однакові рішення.

Збіг двох множин: дві множини A і B називаються рівними, якщо одночасно виконано A⊆B і B⊆A, тобто множина A утримується в множині B і множина B утримується в множині A. Інакше кажучи, дві множини рівні, якщо всі елементи першої належать другій множині, і навпаки. Звідси випливає, що ці множини є тотожніми, складаються з тих самих елементів.

Можна переконатись, що множина [1,2,3] і множина [3,4,5] не тотожні, а множини [1,2,3] і [2,1,3] збігаються.

Якщо множина A є підмножиною множини B, причому в множині В є елементи, що не належать множині А, то говорять, що А — власна підмножина множини В. Позначається цей факт як AÌB. Відповідний предикат може бути визначений з використанням предикатів subset та equal.

prop_subset(A,B):-

Наприклад, множина [1,3] є власною підмножиною множини [1,2,3], на відміну від множин [1,4] і [2,1,3].

Симетрична різниця двох множин є множина, чиї елементи або належать першій і не належать другій множині, або належать другій і не належать першій множині. Симетрична різниця множин A і B позначається через AΔB та у теорії множин визначається таким чином:

AΔB={x|(xÎA & xÏB) або (xÎB & xÏA)}.

На відміну від звичайної різниці, симетрична різниця не залежить від порядку її аргументів - якщо аргументи поміняти місцями, результат залишиться незмінним (AΔB=BΔA), тобто вона коммутативна.

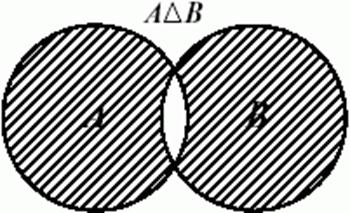
Рис. 5. Симетрична різниця множин А і В

Так, при A={1,2,3,4}, B={3,4,5}, AΔB=BΔA={1,2,5}.

Скористаємося тим, що симетричну різницю можна виразити через уже реалізовані операції:

AΔB=(A\B)È(B\A),

що читається, як симетрична різниця двох множин є різниця між першою і другою множинами, об'єднана з різницею між другою й першою множинами:

sim_minus(A,B,SM):- minus(A,B,A_B),

Дата добавления: 2014-01-11