
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Статистическая обработка результатов многократных измерений
|
|
|
|
На практике приходится иметь дело не с генеральной совокупностью, а с конечной выборкой Х1,Х2,...,Хn. Для определения оценок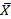 , d(x) пользуются соответственно:
, d(x) пользуются соответственно:
1) среднеарифметическим выборки
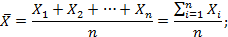
2) дисперсией выборки

3) дисперсией среднего арифметического значения выборки

4) среднеквадратичным значением выборки

Может оказаться, что некоторые значения Хэ из выборки будут представляться слишком большими или слишком маленькими по сравнению с другими измерениями. В этом случае необходимо проверить, не являются ли эти Хэ промахами. Чтобы ответить на вопрос можно ли эти значения учитывать при расчетах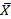 , σX, необходимо для каждого Хэ рассчитать
, σX, необходимо для каждого Хэ рассчитать

и сравнить полученные значения с табличными значениями ξ2 (t - критерия Стьюдента). Табличное значение критерия Стьюдента определяется в зависимости от числа степеней свободы (п – 1) для выбранной доверительной вероятности α. Доверительная вероятность определяет степень достоверности прогнозируемого результата и задается до начала операции прогнозирования.
Если r >ξ2, то Хэ необходимо исключить из дальнейшего рассмотрения. После этого необходимо пересчитать значения 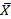 и D (X).
и D (X).
Понятно, что конечный размер выборки не позволяет считать, что X0 = 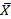 . Можно лишь утверждать, что с некоторой с заранее заданной (доверительной) вероятностью (величина | Х0 -
. Можно лишь утверждать, что с некоторой с заранее заданной (доверительной) вероятностью (величина | Х0 - 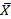 |<
|< , где
, где  характеризует точность оценки
характеризует точность оценки 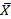 . Интервал
. Интервал  , равный
, равный  , называется доверительным интервалом. При расчетах оценок погрешностей доверительная вероятность должна быть задана (выбрана) заранее.
, называется доверительным интервалом. При расчетах оценок погрешностей доверительная вероятность должна быть задана (выбрана) заранее.
Опыт измерений в технике показывает, что при оценке их точности вполне достаточна доверительная вероятность α, равная 0,95. Поэтому в дальнейшем будем считать, что α =0,95 (т.е. 95 % результатов измерений должны укладываться в доверительный интервал). Иногда для оценки достоверности результатов вероятностно-статистических прогнозов используют показатель, называемый уровнем значимости. Уровень значимости р показывает, какая доля выборки статистически значимо влияет на прогнозируемый результат. С другой стороны, уровень значимости указывает вероятность того, что реальный результат может не соответствовать результатам прогнозирования. Уровень значимости определяется как р=1-α.
В этом случае предельные погрешности отдельного измерения δ х и предельная погрешность среднеарифметического значения 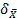 определяются по формулам:
определяются по формулам:
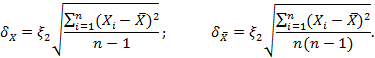
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 454; Нарушение авторских прав?; Мы поможем в написании вашей работы!