
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Распределение населения региона по децильным группам душевого дохода в 2003г
|
|
|
|
| Номер груп-пы | Средне-душевой доход | Доля групп-пы в числ-ти, % | Доля группы в доходах,% | Сред-ний доход в группе | Отклоне-ние группо-вой средней от общей | Квад-раты отклоне-ний | Раз-ность долей | Накоп-ленная доля дохо-дов,% |
| №№ п/п | (руб/чел) | fi | di | xi | xi - 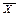
| (xi - 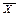 )2 )2
| di – fi | Σxi |
| До 702 | 10% | 2,4% | -1598,5 | -7,6% | 2,4% | |||
| 702-853 | 10% | 3,7% | -1325,5 | -6,3% | 6,1% | |||
| 853-1055 | 10% | 4,6% | -1135,5 | -5,4% | 10,7% | |||
| 1055-1256 | 10% | 5,5% | -946,5 | -4,5% | 16,2% | |||
| 1256-1509 | 10% | 6,5% | -736,5 | -3,5% | 22,7% | |||
| 1509-1850 | 10% | 8,0% | -420,5 | -2,0% | 30,7% | |||
| 1850-2318 | 10% | 10,1% | 20,5 | 0,1% | 40,8% | |||
| 2318-2794 | 10% | 12,0% | 420,5 | 2,0% | 52,8% | |||
| 2794-3652 | 10% | 14,9% | 1031,5 | 4,9% | 67,7% | |||
| Свыше 3652 | 10% | 32,3% | 4690,5 | 22,3% | 100,0% | |||
| Итого: | 100% | 100,0% |
В таблице 6.2. девять чисел (702, 853, 1055, 1256, 1509, 1850, 2318, 2794, 3652) являются соответственно первым, вторым, третьим, четвертым,, пятым, шестым, седьмым, восьмым и девятым децилями. При этом значение пятого дециля совпадает со значением медианы распределения.
На основании данных таблицы 6.2. можно сравнить структурные показатели численности населения, с одной стороны, и доходов, с другой. Например, 10% беднейшего населения региона, т.е. первая децильная группа, имеет лишь 2,4% всех доходов, а 10% наиболее обеспеченного населения имеют 32,3% всех доходов, т.е. в 13,4 раза больше.
Отношение суммарного объема доходов богатейшего населения к суммарному объему доходов беднейшего населения называется коэффициентом фондовой дифференциации или дифференциации фондов. В рассмотренном примере этот коэффициент равен 13,4.
Коэффициент дифференциации фондов может рассчитываться не только для анализа дифференциации доходов, но при анализе неравномерности распределения любого суммарного показателя по равночисленным группам, выделенным в соответствии с величиной некоего другого признака.
Отношение нижней границы доходов богатейшего населения, т.е. девятого дециля, к верхней границе доходов беднейшего населения, т.е. к первому децилю, называется децильным коэффициентом дифференциации.
Общая формула для расчета этого показателя имеет вид:
КD = D9/D1
При анализе распределения полезно сравнить среднюю арифметическую величины душевого дохода с медианой и модой распределения. По данным таблицы 6.2 средняя арифметическая величины душевого дохода равна: 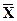 = ΣXi /10 =2103руб/чел.
= ΣXi /10 =2103руб/чел.
Медиана находится на границе 50% менее обеспеченных и 50% более обеспеченных, то есть совпадает с величиной пятого дециля: Me = 1509 руб/чел. Имеет место ярко выраженная правосторонняя асимметрия распределения доходов.
Одним из показателей неравномерности распределения доходов может являться коэффициент вариации, который оценивает степень неоднородности статистической совокупности. В нашем примере этот коэффициент равен отношению σ /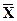 (выраженному в процентах), где σ – среднеквадратическое отклонение, рассчитываемое по формуле:
(выраженному в процентах), где σ – среднеквадратическое отклонение, рассчитываемое по формуле:
σ =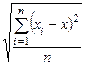
Отсюда находим σ = 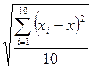 =
=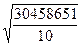 = 1745
= 1745
Коэффициент вариации, соответственно, равен σ /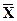 =1745/2103 = 0,83 или 83%, что показывает высокую степень неоднородности статистической совокупности или неравномерности распределения.
=1745/2103 = 0,83 или 83%, что показывает высокую степень неоднородности статистической совокупности или неравномерности распределения.
Специальными показателями оценки степени неравномерности распределения служат коэффициент Лоренца и коэффициент Джини, которые называют обычно показателями концентрации.
Коэффициент вариации не имеет верхней границы и в некоторых случаях может превышать 100%.
Коэффициенты Лоренца и Джини принимают значения в границах от 0 до 1 (или от 0 до 100%), если их выражать в процентах.
Коэффициент Лоренца (L) основан на прямом сравнении долей групп по числу единиц совокупности и долей по объему признака.
По данным табл.6.2, коэффициент Лоренца составил:
L = 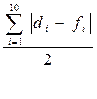 =58,6%/2 = 29,3% = 0,293
=58,6%/2 = 29,3% = 0,293
Порядок расчета коэффициента Джини (G) более сложный.
Формула для его расчета имеет вид:
G = Σ piqi +1 – Σ pi +1 qi,
где pi – накопленные доли численности отдельных групп населения, ранжированных по уровню доходов;
qi – накопленные доли суммарного дохода каждой группы населения.
KD изменяется в пределах от 0 до 1. Обычно, если KD < 0,5, то распределение доходов считается нормальным. По данным таблицы 6.2. получаем: G = 0,399 = 40%.
3. Показатели структурных сдвигов
Показатели структурных сдвигов рассчитываются для анализа изменений структуры статистической совокупности во времени.
Известно много различных вариантов показателей структурных сдвигов, как абсолютных, так и относительных:
Обобщающим абсолютным показателем изменения структуры может служить сумма абсолютных величин (модулей) изменения долей, выраженная в процентных пунктах
Ad = 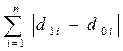
Используется также линейный коэффициент абсолютных структурных сдвигов, представляющий собой сумму модулей изменения долей, деленную на число структурных частей:
Δ = Ad/n = 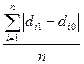
Этот показатель отражает то среднее изменение долей (в процентных пунктах), которое имело место за рассматриваемый период.
Для решения данной задачи используется также квадратический коэффициент абсолютных структурных сдвигов, который резче реагирует на происходящие структурные изменения.
σ = 
Линейный и квадратический коэффициенты абсолютных структурных сдвигов позволяют сводную оценку скорости изменения удельных весов статистической совокупности. Для оценки интенсивности изменения удельных весов используется квадратический коэффициент относительных структурных сдвигов:
kσ = 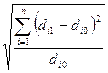
Болгарским исследователем К.Гатевым, а также С.В.Курышевой, Т.Н.Агаповой предложен еще ряд показателей относительного изменения структуры, с которыми можно ознакомиться по дополнительной литературе.
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 1118; Нарушение авторских прав?; Мы поможем в написании вашей работы!