Введение. Лекция №8. Методы и показатели оценки тесноты статистических взаимосвязей

Лекция №8. Методы и показатели оценки тесноты статистических взаимосвязей.

Формулы расчета численности выборки при случайном (или механическом) отборе

Способ отбора	Для средней	Для доли	Для доли, если даже приблизительно она неизвестна
Повторный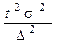
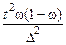
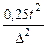
Бесповторный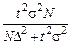

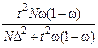
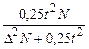
Изучение статистических взаимосвязей занимает наиболее важное место в любом статистическом исследовании, так как статистика – это, прежде всего, наука о количественных закономерностях и взаимосвязях экономических явлений и процессов. Изучение статистических взаимосвязей позволяет выявить факторы (т.е. причины), влияющие на неблагоприятные события в жизни общества и экономике страны, и своевременно принять те или иные меры по регулированию этих процессов. Прежде, чем изучать разнообразные методы оценки статистических взаимосвязей, необходимо разобраться в том, что такое «статистическая взаимосвязь», и чем статистические связи отличаются от других видов взаимосвязей между явлениями.

1. Понятие «статистическая взаимосвязь»

В статистике принято выделять два вида связи между явлениями:

1) функциональные (или детерминированные);

2) статистические (или стохастические).

Для первого вида связи характерна однозначная строго определенная зависимость между взаимосвязанными показателями или признаками.

Для второго вида связи характерно то, что одному значению независимого признака или показателя может соответствовать несколько значений другого (зависимого) признака или показателя. Простейший пример: люди, имеющие одинаковый рост, не обязательно будут иметь одинаковый вес. Предприятия одинакового размера (то есть с одинаковой численностью работающих или одинаковой стоимостью имущества) совсем не обязательно будут иметь одинаковую прибыль или объем выпускаемой продукции. Но в то же время от размера предприятия зависит и объем продукции и его прибыль. Статистические связи обычно проявляются в среднем, массовом масштабе. Например, средний вес более высоких людей больше, чем средний вес более низких, но отдельный, более высокий человек, может иметь более низкий вес, чем другой человек, рост которого меньше.

Обычно, если между какими-то признаками или показателями имеется статистическая зависимость, то одни из них являются независимыми, то есть изменяются независимо от других, а другие, наоборот, зависимыми, то есть их изменения тесно зависят с изменением других. Условно можно считать, что независимые признаки являются причинами (т.е. факторами), а зависимые – следствиями или результатами.

В статистике независимые признаки принято называть факторными, а зависимые – результативными. Статистические связи обычно проявляются в среднем, массовом масштабе. Например, средний вес более высоких людей больше, чем средний вес более низких, но отдельный, более высокий человек, может иметь более низкий вес, чем другой человек, рост которого меньше.

Однако не всякая статистическая связь отражает какую-то причинно-следственную зависимость. Иногда статистическая зависимость может носить случайный характер и не отражать реальную причинно-следственную взаимосвязь. Обычно, обнаружив статистическую зависимость между какими-то процессами или явлениями, ученые выдвигают гипотезу о наличии причинно-следственной зависимости, а потом проверяют эту гипотезу на практике или доказывают ее истинность с помощью других методов.

Статистические связи в статистике часто называют корреляционными (от английского слова «correlation» - отношение или соотношение), а показатели, используемые для оценки степени тесноты статистических связей – показателями корреляции.

Само слово «корреляция» ввел в статистику английский биолог и статистик Френсис Гальтон в конец XIX века. Слово relation непосредственно означает «Связь», а слово «Correlation» значит «Как бы связь», т.е. связь, но не в привычной в то время функциональной форме.

Корреляционная зависимость между различными показателями (или признаками) может возникнуть разными путями.

Первый (важнейший) путь – причинно-следственная зависимость результативного признака и его вариации (изменений) от вариации факторного признака. Например, признак x – балл оценки степени плодородия почвы, а y – уровень урожайности сельскохозяйственной культуры. Здесь совершенно ясно логически, какой признак выступает как независимая переменная (фактор) x, а какой – как зависимая переменная (результат) y.

Дата добавления: 2014-01-20