Аналитические показатели оценки тесноты взаимосвязей между количественными признаками и способы их расчета

Виды аналитических показателей	Формулы для их расчета
Линейный коэффициент корреляции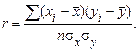
Ранговый коэффициент корреляции
Корреляционное отношение
Индекс детерминации

3. Аналитические показатели оценки тесноты взаимосвязей между количественно измеримыми признаками

В статистике разработано много различных показателей, выражающих тесноту связей между явлениями и процессами, но каждый из них обладает своими преимуществами и недостатками. Наиболее распространенным из них является линейный коэффициент корреляции, но он показывает наличие тесноты связи только в случае, если зависимость между значениями показателей носит линейный характер. Если это не так, лучше пользоваться другими показателями. Показатель так называемого «корреляционного отношения» можно использовать в довольно широкой области, но предварительно необходимо построить уравнение регрессии, описывающее статистическую взаимосвязь между признаками X и Y, т.е. расчет этого показателя довольно сложен[10].

Ранговый коэффициент корреляции может использоваться даже в том случае, если признаки нельзя выразить количественно, но можно проранжировать, то есть расположить по порядку. Существуют также особые способы измерения взаимосвязей между количественно не измеримыми признаками, которые мы рассмотрим ниже.

Линейный коэффициент корреляции рассчитывается по формуле:

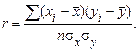
В этой формуле и 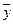– средние значения признаков x и y, а 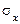и 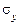– соответственно средние квадратические отклонения. Из этой формулы легко выводятся другие формулы для расчета линейного коэффициента корреляции, например:

Или

Все эти формулы тождественны и дают один и тот же результат, но в разных случаях бывает удобнее пользоваться той или иной формулой. Первая и вторая формула наиболее удобны для запоминания, но расчет по последней формуле более прост.

Для расчета линейного коэффициента корреляции по последней из приведенных формул обычно строится вспомогательная таблица следующего вида (табл. 8.2).

Таблица 8.2

Вспомогательная таблица для расчета линейного
коэффициента корреляции

x	y
…
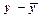
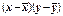
Σ

В последней строке таблицы 8.2. рассчитываются суммы по столбцам.

Линейный коэффициент корреляции равен отношению суммы в последнем столбце таблицы к корню из произведения сумм в двух предшествующих столбцах.

Подчеркнем, что линейный коэффициент корреляции обладает следующим свойством: он всегда находится между –1 и 1, т.е. всегда –1 r 1.

Если при вычислениях вдруг обнаруживается, что коэффициент корреляции находится за пределами этих границ, значит, это просто ошибка в расчетах!

Чем ближе коэффициент корреляции к 1, тем более тесной является связь! При этом если r > 0, то связь прямая, а если r < 0, то связь обратная.

Если | r | ≥ 0,7, то связь считается более тесной, если
| r | < 0,3, то связь отсутствует. Если 0,3 ≤ | r | ≤ 0,7, то наличие связи целесообразно проверить дополнительными методами.

Линейный коэффициент корреляции может не всегда показать наличие связи. В случае, если значения признаков нельзя измерить количественно, удобнее использовать ранговый коэффициент корреляции или специальные коэффициенты, используемые для оценки тесноты связи между качественными признаками. Если связь не является линейной, то в качестве критерия оценки тесноты связи удобнее всего использовать так называемое корреляционное отношение. Но для его расчета вначале необходимо построить так называемое уравнение регрессии[11] (т.е. связи между признаками).

Линейный коэффициент корреляции и корреляционное отношение не являются универсальными показателями оценки тесноты связи. Их можно применять только в том случае, если изучаемые признаки можно измерить количественно.

При использовании этих методов нельзя обойтись без вычисления основных параметров распределения (средних величин, дисперсий). Поэтому методы, основанные на их использовании, получили название параметрических методов оценки тесноты статистической связи.

Между тем в статистической практике приходится сталкиваться с задачами измерения взаимосвязей между качественными признаками, к которым параметрические методы анализа в их обычном виде не применимы. Статистической наукой разработаны методы, которые позволяют оценить тесноту взаимосвязи между явлениями, не используя при этом количественные значения признака, а значит, не рассчитывая и параметры распределения. Такие методы получили название непараметрических.

Одним из таких методов является расчет так называемого рангового коэффициента корреляции. Он может использоваться как в тех случаях, когда признаки измеримы количественно, так и в тех случаях, когда их нельзя измерить количественно, но можно проранжировать, то есть расположить их значения в порядке возрастания. Например, предположим, что при оценке тесноты связи между ростом и весом некоторой группы людей мы по каким-то причинам не смогли достать измерительные приборы (весы, ростомер и т.п.). Но мы можем выстроить этих людей по росту, определив, кто из них выше, а кто ниже, и одновременно определить, кто из них больше весит, усадив их на качели. Таким образом, мы можем проранжировать их рост и вес. Ранг – это порядковый номер значений признака, расположенных по их возрастанию. Если нам известны количественные значения соответствующих признаков, то в расчетах рангового коэффициента корреляции они все равно не понадобятся – нужно только определить ранг соответствующего значения.

Предположим, что мы расположили значения признаков x и y порядку и перенумеровали их, то есть присвоили каждому соответствующий порядковый номер или ранг. (Необходимо отметить, что одинаковым значениям присваивается одинаковый ранг!)

Обозначим ранг значения признака как p_x а ранг значения признака y как p_y

Формула для расчета рангового коэффициента корреляции имеет вид:

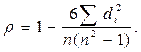
В этой формуле d_i – это разность рангов значений признаков x и y, то есть d_i= p_xi- p_yi

Для расчета рангового коэффициента корреляции удобно построить вспомогательную таблицу (табл. 8.3).

Таблица 8.3

Вспомогательная таблица для расчета рангового
коэффициента корреляции Спирмена

№ п/п	x	y	px (ранг x)	py (ранг y)	di= pxi- pyi (разность рангов)	di ^2
…
Σ	–	–	–	–	–	-

Значения рангового коэффициента корреляции также расположены между «–1» и 1, как и линейного коэффициента корреляции, но обычно ранговый коэффициент измеряет тесноту связи более «грубо» (приближенно), чем линейный.

Сам по себе ранговый коэффициент Спирмена называют еще коэффициентом корреляции рангов, потому что формулу для его расчета можно вывести из обычной формулы для линейного коэффициента корреляции. Предположим, что мы проранжировали признаки X и Y, а потом рассчитали коэффициент корреляции между их рангами по формуле:

где p_xi - ранг i-той единицы совокупности по переменной x;

p_yi - ранг i-той единицы совокупности по переменной y;

- средний ранг по переменной x; 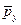- средний ранг по переменной y.

Известно, что сумма квадратов отклонений чисел натурального ряда от их средней величины равна (n³-n)/12. Так как ранги представляют собой ряд натуральных чисел, то 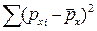= (n³-n)/12 и= (n³-n)/12 т.е.в знаменателе формулы стоит величина (n³-n)/12.

Преобразуя формулу рангового коэффициента корреляции, получаем:

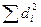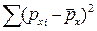= = + - 2= 2×((n³-n)/12)- 2= (n³-n)/6− 2

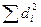Отсюда получаем, что = ((n³-n)/6− ): 2

И, следовательно,

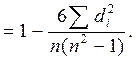
Помимо коэффициента Спирмена в статистике используют также коэффициент корреляции рангов Кендэлла (τ), который рассчитывается по формуле:

Где n – число наблюдений, а S – сумма разностей между числом последовательностей и числом инверсий по второму признаку. Чтобы рассчитать этот коэффициент, выполняют несколько последовательных этапов:

1) Значения X ранжируются в порядке возрастания или убывания;

2) Значения Y располагаются в порядке, соответствующем значениям X;

3) Для каждого ранга Y определяется число следующих за ним значений рангов, превышающих его величину. Сумма всех этих чисел (обозначается через P) определяется как мера соответствия последовательностей рангов по X и Y и учитывается со знаком (+);

4) Для каждого ранга Y определяется число следующих за ним значений рангов, меньших его величины. Сумма этих чисел обозначается через Q и учитывается со знаком (-);

5) Находится сумма баллов по всем членам ряда S = P-Q;

6) Полученная сумма соотносится с максимально возможной, которая равна n(n-1) /2 в случае если в обоих рядах ранги следуют строго последовательно от 1 до n.

Дата добавления: 2014-01-20