
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Методы решения задач. Примеры решения задач
|
|
|
|
В динамике можно выделить две основные задачи:
1) нахождение сил, под действием которых может происходить данное движение тела;
2) определение кинематических характеристик движения тела, когда известны действующие на него силы.
Любую задачу динамики рекомендуется решать по следующему алгоритму:
1. Сделать чертеж. На чертеже указать направление движения тела (направление скорости 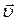 ) и направление ускорения
) и направление ускорения 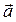 .
.
2. Указать силы, действующие на тело. Записать второй закон Ньютона в векторной форме: 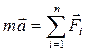 .
.
3. Выбрать направление координатных осей 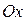 и
и 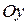 и спроецировать на них записанное ранее векторное уравнение.
и спроецировать на них записанное ранее векторное уравнение.
4. Если в движении участвует несколько взаимно связанных тел, то необходимо для каждого из них выполнить п. 1–3.
5. Решить полученную систему уравнений.
Часто в условиях задачи содержится дополнительная информация. В частности, слово «легкая» нить означает, что ее масса равна нулю, «нерастяжимая» нить – удлинением нити можно пренебречь, «гладкий» стол – трение отсутствует. Практически всегда удобно за положительное направление одной координатной оси выбрать направление ускорения тела (вторая ось перпендикулярна этому направлению).
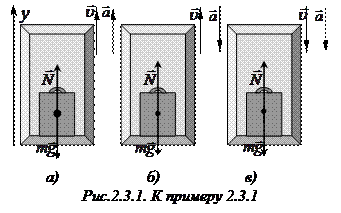
 Пример 2.3.1. Чемодан массой
Пример 2.3.1. Чемодан массой 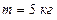 стоит на полу лифта, движущегося с ускорением
стоит на полу лифта, движущегося с ускорением 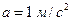 . Найти вес чемодана, если 1) лифт движется вверх равноускоренно; 2) лифт движется вверх равнозамедленно; 3) лифт движется вниз равноускоренно; 4) свободно падает.
. Найти вес чемодана, если 1) лифт движется вверх равноускоренно; 2) лифт движется вверх равнозамедленно; 3) лифт движется вниз равноускоренно; 4) свободно падает.
 Дано: Решение:
Дано: Решение:
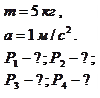
 На чемодан действует сила тяжести
На чемодан действует сила тяжести 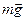 и сила нормальной реакции опоры
и сила нормальной реакции опоры  . Вес тела
. Вес тела 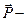 это сила, с которой чемодан давит на пол кабины лифта (приложена к лифту). По третьему закону Ньютона он численно равен силе, с которой опора действует на чемодан, т.е.
это сила, с которой чемодан давит на пол кабины лифта (приложена к лифту). По третьему закону Ньютона он численно равен силе, с которой опора действует на чемодан, т.е. 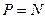 . Следовательно, для нахождения веса чемодана необходимо найти численное значение силы реакции опоры. Сделаем чертеж, на котором укажем силы, действующие на чемодан, направление движения (направление скорости
. Следовательно, для нахождения веса чемодана необходимо найти численное значение силы реакции опоры. Сделаем чертеж, на котором укажем силы, действующие на чемодан, направление движения (направление скорости 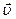 ), направление ускорения
), направление ускорения 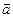 .
.
Решим задачу в инерциальной системе отсчета, связанной с землей. Ось координат Оу
направим вертикально вверх (рис. 2.3.1).
1) пусть лифт движется равноускоренно вверх (рис. 2.3.1.а). По второму закону Ньютона 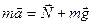 ; в проекции на ось Оу:
; в проекции на ось Оу: 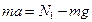 , откуда
, откуда 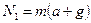 . Следовательно, вес чемодана
. Следовательно, вес чемодана 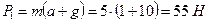 .
.
2) пусть лифт движется равнозамедленно вверх – направления скорости и ускорения противоположны (рис. 2.3.1.б). По второму закону Ньютона 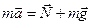 ; в проекции на ось Оу:
; в проекции на ось Оу: 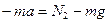 , откуда
, откуда 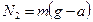 . Следовательно, вес чемодана
. Следовательно, вес чемодана 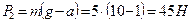 .
.
3) пусть лифт движется равноускоренно вниз (рис. 2.3.1.в). По второму закону Ньютона 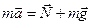 ; в проекции на ось Оу:
; в проекции на ось Оу: 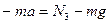 , откуда
, откуда 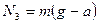 .
.
Следовательно, вес чемодана 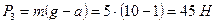 .
.
4) пусть лифт свободно падает. Ускорение лифта равно ускорению свободного падения, т.е. 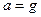 . По второму закону Ньютона
. По второму закону Ньютона 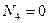 , следовательно,
, следовательно,  (состояние невесомости).
(состояние невесомости).
Ответ: 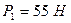 ,
, 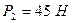 ,
, 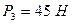 ,
,  .
.
Таким образом, вес тела зависит от ускорения (модуля и направления), с которым движется опора. Направление и величина скорости на вес не влияют показания.
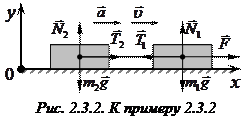
Пример 2.3.2. Два тела с массами 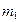 и
и 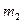 , связанные легкой нерастяжимой нитью, движутся по гладкому столу под действием горизонтальной силы
, связанные легкой нерастяжимой нитью, движутся по гладкому столу под действием горизонтальной силы 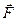 . Найти силу натяжения нити и ускорение тел.
. Найти силу натяжения нити и ускорение тел.
 Дано: Решение:
Дано: Решение:
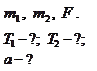
 На чертеже укажем силы, действующие на каждое тело, направление скорости и ускорения (рис. 2.3.2). Решать задачу будем в инерциальной системе отсчета, связанной со столом.
На чертеже укажем силы, действующие на каждое тело, направление скорости и ускорения (рис. 2.3.2). Решать задачу будем в инерциальной системе отсчета, связанной со столом.
Поскольку нить невесома, то из уравнения движения нити 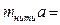
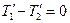 , где
, где 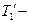 сила, с которой первое тело действует на нить (приложена к нити и по третьему закону Ньютона равна силе
сила, с которой первое тело действует на нить (приложена к нити и по третьему закону Ньютона равна силе 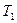 , с которой нить действует на первое тело);
, с которой нить действует на первое тело);  сила, с которой второе тело действует на нить (приложена к нити и по третьему закону Ньютона равна
сила, с которой второе тело действует на нить (приложена к нити и по третьему закону Ньютона равна 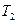 ).
).
Т.к. 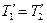 , то
, то 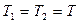 . Тогда уравнения движения тел имеют вид:
. Тогда уравнения движения тел имеют вид: 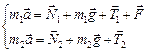 . В проекции на ось Ох:
. В проекции на ось Ох: 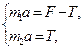 откуда
откуда 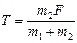 и
и 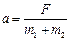 .
.
Ответ: 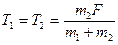 ,
, 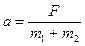 .
.
Пример 2.3.3. К пружинным весам подвешен блок. Через блок перекинут шнур, к концам которого привязаны грузы массой 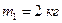 и
и 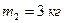 . Каково будет показание весов во время движения грузов? Массой блока и шнура пренебречь. Шнур считать нерастяжимым.
. Каково будет показание весов во время движения грузов? Массой блока и шнура пренебречь. Шнур считать нерастяжимым.
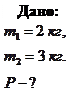
 Решение:
Решение:
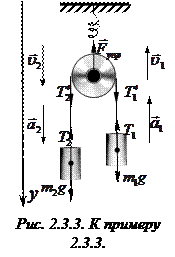
 Направления движения, направления ускорений и сил, действующих на грузы и блок в процессе движения, показаны на рис. 2.3.3. Запишем II закон
Направления движения, направления ускорений и сил, действующих на грузы и блок в процессе движения, показаны на рис. 2.3.3. Запишем II закон  Ньютона для трех тел, участвующих в движении:
Ньютона для трех тел, участвующих в движении: 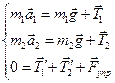 .
.
Ось Оу направим вертикально вниз и спроецируем на нее векторные уравнения. Т.к. нить нерастяжима, то за одно и то же время грузы проходят одинаковый путь, откуда следует, что 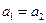 . В проекции на ось Оу:
. В проекции на ось Оу: 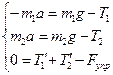 .
.
Т.к. тела связаны невесомой нитью (масса блока тоже не учитывается), то силу натяжения нити считают одинаковой по всей длине 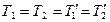 , следовательно
, следовательно 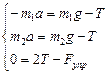 . Вычтем из среднего уравнения верхнее:
. Вычтем из среднего уравнения верхнее: 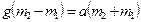 , откуда
, откуда 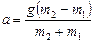 .
.
Подставим полученное значение в верхнее уравнение системы и выразим силу натяжения 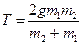 . Из третьего уравнения
. Из третьего уравнения 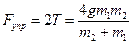 .
.
Т.к. по определению вес численно равен силе, с которой растянута пружина, то 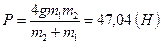 .
.
Ответ: 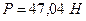 .
.
Пример 2.3.4. На наклонную плоскость, образующую угол 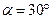 с горизонтом, поставлен кирпич. Коэффициент трения
с горизонтом, поставлен кирпич. Коэффициент трения 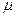 между кирпичом и плоскостью равен
между кирпичом и плоскостью равен 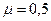 . С каким ускорением кирпич будет соскальзывать с плоскости? При каких значениях
. С каким ускорением кирпич будет соскальзывать с плоскости? При каких значениях  коэффициента трения кирпич останется в покое?
коэффициента трения кирпич останется в покое?

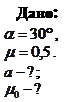 Решение:
Решение:
 Действующие на кирпич силы, направления скорости
Действующие на кирпич силы, направления скорости 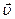 и ускорения
и ускорения 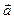 изображены на рис. 2.3.4. Задачу решаем в инерциальной системе отсчета, связанной с наклонной плоскостью. Ось Ох направим по направлению ускорения кубика, ось Оу - перпендикулярно ей. Второй закон Ньютона для кирпича имеет вид:
изображены на рис. 2.3.4. Задачу решаем в инерциальной системе отсчета, связанной с наклонной плоскостью. Ось Ох направим по направлению ускорения кубика, ось Оу - перпендикулярно ей. Второй закон Ньютона для кирпича имеет вид: 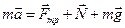 . В проекции на координатные оси
. В проекции на координатные оси 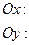

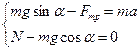 .
.
При скольжении сила трения 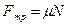 , поэтому
, поэтому 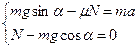 .
.
Решая систему уравнений, находим: 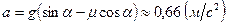 .
.
Кирпич не будет скользить, если максимальная сила трения покоя 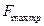 больше (или равна) проекции силы тяжести на направление Ох:
больше (или равна) проекции силы тяжести на направление Ох: 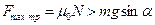 или
или 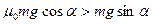 , откуда
, откуда 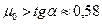 .
.
Ответ:  ,
, 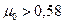 .
.
 Пример 2.3.5. Автомобиль массой
Пример 2.3.5. Автомобиль массой  пытается въехать без предварительного разгона на гору с углом наклона
пытается въехать без предварительного разгона на гору с углом наклона 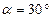 , коэффициент трения между шинами автомобиля и поверхностью горки
, коэффициент трения между шинами автомобиля и поверхностью горки 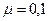 . С каким ускорением будет двигаться автомобиль? Считать все колеса ведущими.
. С каким ускорением будет двигаться автомобиль? Считать все колеса ведущими.
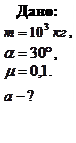
 Решение:
Решение:
 На рис. 2.3.5 показаны силы, действующие на автомобиль на наклонной плоскости. (Учли, что сила трения – внешняя сила, обеспечивающая ускорение автомобиля). Максимальная сила трения (см. пример 2.3.3)
На рис. 2.3.5 показаны силы, действующие на автомобиль на наклонной плоскости. (Учли, что сила трения – внешняя сила, обеспечивающая ускорение автомобиля). Максимальная сила трения (см. пример 2.3.3)
 .
.
С другой стороны, препятствующая движению составляющая силы тяжести численно равна 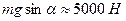 .
.
Видим, что 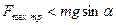 . То есть при любой силе тяги машина не может въехать в гору, колеса будут пробуксовывать. Ускорение автомобиля будет равно нулю.
. То есть при любой силе тяги машина не может въехать в гору, колеса будут пробуксовывать. Ускорение автомобиля будет равно нулю.
|
|
|
|
|
Дата добавления: 2014-01-20; Просмотров: 1648; Нарушение авторских прав?; Мы поможем в написании вашей работы!