Неинерциальные системы отсчета. Силы инерции

Законы Ньютона выполняются только в инерциальных системах отсчета. Найдем уравнение движения тела в неинерциальной системе отсчета.

Пусть неинерциальная система отсчета движется поступательно относительно инерциальной системы с ускорением 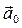. Обозначим ускорение материальной точки в инерциальной системе 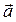, ускорение материальной точки в неинерциальной системе 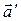. Очевидно, что разность ускорений точки: 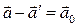, откуда .

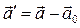Ускорение тела в инерциальной системе отсчета находится по второму закону Ньютона: 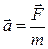. Тогда ускорение тела в неинерциальной системе отсчета .

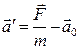Отсюда следует, что даже при 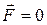тело будет двигаться по отношению к неинерциальной системе отсчета с ускорением 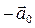, т.е. так, как если бы на него действовала сила 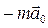. Силу, равную этой величине, называют силой инерции

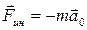. (2.4.1)

Соответственно, второй закон Ньютона в неинерциальной системе отсчета будет иметь вид:

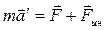. (2.4.2)

Проявление сил инерции при поступательно движении наблюдается в повседневных явлениях. Например, когда автомобиль набирает скорость, пассажир под действием силы инерции прижимается к спинке сидения. При торможении сила направлена в противоположную сторону и пассажир удаляется от спинки сидения. При запуске космических кораблей силы инерции вызывают перегрузки.

Таким образом, при описании движения в неинерциальных системах отсчета можно пользоваться законами Ньютона, если наряду с силами, обусловленными действием тел друг на друга, учитывать силы инерции.

Следует понимать, что силы инерции – фиктивные силы: они исчезают в инерциальных системах отсчета.

Пусть неинерциальная система отсчета вращается по отношению к инерциальной с угловой скоростью 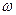. Тогда на любое тело в этой системе, независимо от того, покоится оно или движется, действует центробежная сила инерции:

,

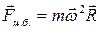где 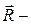радиус-вектор, проведенный к телу из центра вращения. Центробежная сила инерции направлена перпендикулярно оси вращения от центра.

В качестве примера рассмотрим шарик массы 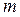на пружине, закрепленной в центре диска. Диск может вращаться вокруг вертикальной оси с угловой скоростью

(рис. 2.4.1). Если диск неподвижен (система отсчета, связанная с ним, является инерциальной), то пружина не растянута 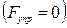. При вращении диска (система отсчета, связанная с ним, становится неинерциальной) пружина растягивается. Сила упругости уравновешивается возникающей центробежной силой инерции:

.

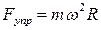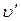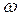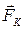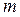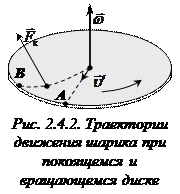
Пусть тело движется с постоянной скоростью относительно равномерно вращающейся с угловой скоростью неинерциальной системы отсчета. Тогда кроме центробежной силы инерции на него будет действовать кориолисова сила инерции , направленная перпендикулярно скорости тела. Например, сообщим шарику массой скорость 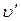вдоль радиуса диска. Если диск не вращается, то шарик движется по радиальной прямой и попадает в точку А (рис. 2.4.2). Если диск привести во вращение в направлении, указанном стрелкой, то шарик покатится по кривой и попадет в точку В, т.е. будет двигаться так, как если бы на него действовала сила, перпендикулярная вектору скорости.

Вектор 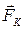перпендикулярен векторам скорости тела 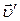и угловой скорости вращения системы отсчета (связан с ним правилом буравчика) и равен .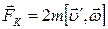

Действием кориолисовой силы инерции, возникающей вследствие суточного вращения Земли, у рек, текущих в северном полушарии вдоль меридиана с юга на север, подмывается правый берег, в южном – левый; при выстреле на север снаряд будет отклоняться к востоку в северном полушарии и к западу в южном; при стрельбе вдоль экватора будет прижиматься к Земле, если выстрел производить на запад, и т.д.

Продемонстрируем, как можно пользоваться законом Ньютона при решении задач в неинерциальных системах отсчета.

Пример 2.4.1. Решим задачу 2.3.1 в неинерциальной системе отсчета, связанной с движущимся ускоренно лифтом (ранее она решалась в инерциальной системе отсчета, связанной с Землей).

Решение:

Для описания движения чемодана можно использовать второй закон Ньютона, если наряду с реальными силами (силой тяжести и силой реакции опоры) учесть действующую на чемодан силу инерции 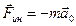, где 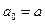(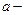ускорение движущейся вместе с лифтом системы отсчета относительно Земли).

1) Пусть лифт движется равноускоренно вверх (рис. 2.4.3.а). Относительно кабины

лифта чемодан покоится 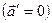, следовательно, 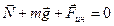. Учитывая, что 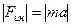, в проекции на о сь 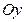: 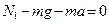, откуда 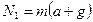. Вес чемодана .

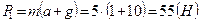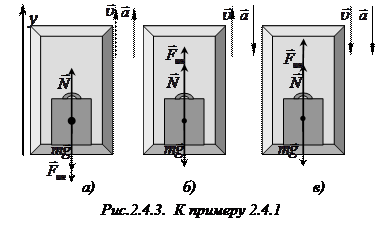
2) Пусть лифт движется равнозамедленно вверх (рис. 2.4.3.б). 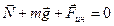. В проекции на ось 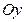: 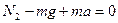, откуда 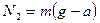. Вес чемодана .

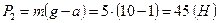3) Пусть лифт движется равноускоренно вниз (рис. 2.4.3.в). 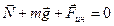. В проекции на ось 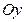: 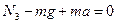, откуда 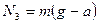. Вес чемодана .

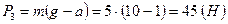4) Пусть лифт свободно падает. Ускорение лифта равно ускорению свободного падения, т.е. 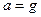. По второму закону Ньютона 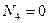, следовательно, (состояние невесомости).

Ответ: , , , .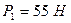

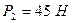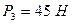Таким образом, полученный результат совпадает с результатом решения в инерциальной системе отсчета.

Пример 2.4.2. К потолку вагона, движущегося в горизонтальном направлении с ускорением 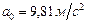, подвешен на нити шарик массой 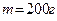. Определите для установившегося движения: 1) силу натяжения нити 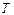; 2) угол 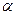отклонения нити от вертикали.

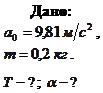
Решение:

Задачу решим в неинерциальной системе отсчета, связанной с движущимся ускоренно вагоном. Кроме реальных сил (силы натяжения нити 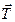и силы тяжести 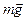) на шарик будет действовать сила инерции .

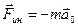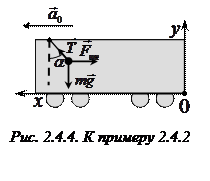
В системе отсчета, связанной с вагоном, уравнение движения шарика имеет вид: 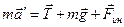. Спроецируем это уравнение на координатные оси Ох и Оу (рис. 2.4.4), учтя, что в неинерциальной системе отсчета, связанной с вагоном, шарик покоится : .

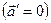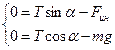Поскольку сила инерции в этом случае 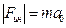, то .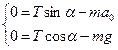

Решая систему уравнений, получим 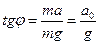, откуда .

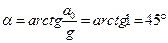Тогда .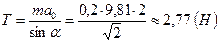

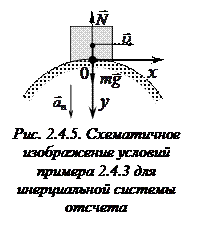
Ответ: , .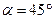

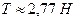Пример 2.4.3. Автомобиль массой 5 т движется со скоростью 10 м/с по выпуклому мосту. Определить силу давления автомобиля на мост в его верхней части, если радиус кривизны моста 50 м. Задачу решить в инерциальной и неинерциальной системах отсчета.

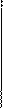
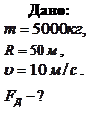Решение:

1) В инерциальной системе отсчета, связанной с мостом, на автомобиль действуют две силы: сила реакции опоры 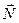и сила тяжести .

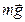Так как автомобиль движется по окружности с постоянной скоростью, то 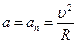(вектор направлен к центру кривизны моста).

Уравнение движения в системе отсчета, связанной с неподвижным мостом: 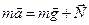(рис. 2.4.5). В проекции на координатную ось Oy уравнение движения имеет вид: 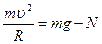, откуда .

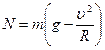По третьему закону Ньютона сила 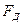, с которой автомобиль давит на мост, численно равна силе 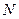, с которой мост действует на автомобиль.

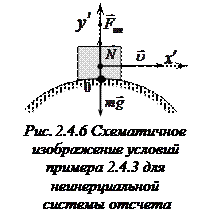Следовательно,.

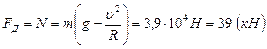2) В неинерциальной системе отсчета, связанной с движущимся по окружности автомобилем, кроме сил тяжести 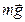и реакции опоры 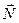, на автомобиль действует центробежная сила инерции 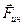, направленная от центра кривизны моста и равная (рис. 2.4.6).

Уравнение движения автомобиля в неинерциальной системе отсчета имеет вид: .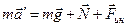

В этой системе отсчета автомобиль покоится 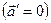. Следовательно, .

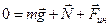В проекции на ось Oy: 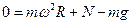, откуда 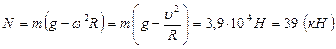. Т.к. 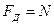, то .

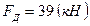Ответ: .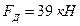

Дата добавления: 2014-01-20