Неформальное описание игры

Всякая игра предполагает следующее:

1. Наличие некоторого числа n участвующих в ней лиц (игроков). Могут быть игры с одним игроком (пасьянс), двумя игроками (шахматы, муж с женой, две конкурирующие фирмы), тремя игроками (преферанс, три фирмы на рынке) и т.д. По числу игроков и идёт классификация игр - игры двух лиц, трёх лиц и т.д.;
2. Конечный выигрыш (или проигрыш) каждого игрока. Когда игра кончается, каждый игрок получает доход (если 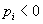- значит, игрок проиграл), зависящий от его поведения и поведения других игроков.

Наиболее изученным классом игр являются так называемые игры с нулевой суммой, когда в любой партии имеет место условие

,

то есть если кто-то выигрывает, то кто-то обязательно проигрывает. Это особенно проявляется в играх двух лиц с нулевой суммой, когда , то есть . В этом случае интересы игроков строго противоположны, так как выигрыш одного игрока является одновременно проигрышем другого. Такие игры называют антагонистическими.

Всякая игра состоит из партий, которые начинаются и заканчиваются, после чего игрокам выплачиваются их выигрыши. В свою очередь, каждая партия состоит из ходов, которые одновременно или последовательно делают игроки. Описание игры как последовательности ходов носит название позиционной формы игры. Теория игр в позиционной форме разработана очень слабо и ещё ждёт своих Эйлеров и Гауссов.

Основное содержание современной теории игр - это так называемая матричная форма игры. В этом случае считается, что каждый игрок делает всего лишь один ход, причем все ходы делаются одновременно. После этого каждому игроку выплачивается выигрыш (или берётся проигрыш) в зависимости от того, какие ходы были сделаны им и другими игроками.

Вообще говоря, игра в позиционной форме может быть сведена к игре в матричной форме, однако для реальных игр это сведение настолько сложно, что практически невыполнимо даже для современных ЭВМ. Однако вполне возможно, что в будущем такое сведение будет иметь и практический смысл.

Дата добавления: 2014-01-20