Вероятность появления хотя бы одного события

Пусть в результате испытания могут появиться n событий, независимых в совокупности, либо некоторые из них (в частности, только одно или ни одного), причем вероятности появления каждого из событий известны. Как найти вероятность того, что наступит хотя бы одно из этих событий? Например, если в результате испытания могут появиться три события, то появление хотя бы одного из этих событий означает наступление либо одного, либо двух, либо трех событий. Ответ на поставленный вопрос дает следующая теорема.

Теорема. Вероятность появления хотя бы одного из событий А ₁, А ₂,..., А_n, независимых в совокупности, равна разности между единицей и произведением, вероятностей противоположных событий :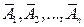

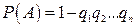. (2.14)

Доказательство. Обозначим через А событие, состоящее в появлении хотя бы одного из событий А ₁, А ₂,..., А_n. События А и (ни одно из событий не наступило) противоположны, следовательно, сумма их вероятностей равна единице:

.

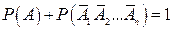Отсюда, пользуясь теоремой умножения, получим

,

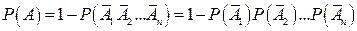или

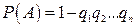
Частный случай. Если события А ₁, А ₂,..., А_n имеют одинаковую вероятность, равную р, то вероятность появления хотя бы одного из этих событий

. (2.15)

Пример. Вероятности попадания в цель при стрельбе из трех орудий таковы: р ₁ = 0,8; р ₂ = 0,7; р ₃ = 0,9. Найти вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий.

Решение. Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому рассматриваемые события A ₁ (попадание первого орудия), А ₂ (попадание второго орудия) и А ₃ (попадание третьего орудия) независимы в совокупности.

Вероятности событий, противоположных событиям А ₁, А ₂ и А ₃ (т.е. вероятности промахов), соответственно равны:

q _l =1 – p _l = 1 – 0,8 = 0,2;

q ₂ =1 – p ₂ = 1 – 0,7 = 0,3;

q ₃ =1 – p ₃ = 1 – 0,9 = 0,1.

Искомая вероятность

.

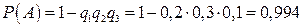Пример. В типографии имеется 4 плоскопечатных машины. Для каждой машины вероятность того, что она работает в данный момент, равна 0,9. Найти вероятность того, что в данный момент работает хотя бы одна машина (событие А).

Решение. События «машина работает» и «машина не работает» (в данный момент) – противоположные, поэтому сумма их вероятностей равна единице:

p + q = 1.

Отсюда вероятность того, что машина в данный момент не работает, равна

q – p = 1 – 0.9 = 0.1.

Искомая вероятность

Р (A)= 1 – q ⁴ = 1 – 0,1⁴ = 0,9999.

Так как полученная вероятность весьма близка к единице, то на основании следствия из принципа практической невозможности маловероятных событий мы вправе заключить, что в данный момент работает хотя бы одна из машин.

Пример. Вероятность того, что при одном выстреле стрелок попадает в цель, равна 0,4. Сколько выстрелов должен произвести стрелок, чтобы с вероятностью не менее 0,9 он попал в цель хотя бы один раз?

Решение. Обозначим через А событие «при n выстрелах стрелок попадает в цель хотя бы един раз». События, состоящие в попадании в цель при первом, втором выстрелах и т.д., независимы в совокупности, поэтому применима формула (2.15). Приняв во внимание, что, по условию, Р (A) ³ 0,9, p = 0,4 (следовательно, q = 1 – 0,4 = 0,6), получим

1 – 0,6 ⁿ ³ 0,9; отсюда 0,6 ⁿ £ 0,1.

Прологарифмируем это неравенство по основанию 10:

n lg 0,6 £ lg 0,1.

Отсюда, учитывая, что lg 0,6 < 0, имеем

.

Итак, n ³ 5, т.е. стрелок должен произвести не менее 5 выстрелов.

Пример. Вероятность того, что событие появится хотя бы один раз в трех независимых в совокупности испытаниях, равна 0,936. Найти вероятность появления события в одном испытании (предполагается, что во всех испытаниях вероятность появления события одна и та же).

Решение. Так как рассматриваемые события независимы в совокупности, то применима формула (2.15). По условию, Р (А) =0,936; n = 3. Следовательно,

0,936 =1 – q ³, или q ³ = 1 – 0,936 = 0,064.

Отсюда . Искомая вероятность

р = 1 – q =1 – 0,4 = 0,6.

Дата добавления: 2014-01-20