Множество Жюлиа

Лекция 13

Секованов В.С., Миронкин Д.П.

Многие замечательные свойства фракталов открываются при изучении итерированных отображений.

При этом начинают с некоторой функции y=f(x) и рассматривают поведение последовательности f(x), f(f(x)), f(f(f(x))),…

Замечательного прогресса в изучении итерированных функций на комплексной плоскости добились Гастон Жюлиа и Пьер Фату в 1918 году. Французский математик Гастон Жюлиа исследовал свойства отображения на комплексной плоскости и получил множества с помощью итерированных функций. Позднее эти множества получили название «множества Жюлиа».

Множество Жюлиа для функции комплексного переменного , обозначаемое , определяется как , где - граница области притяжения бесконечности, а .

Другими словами, множество Жюлиа функции есть граница множества точек z, стремящихся к бесконечности при итерировании f(z).

Рассмотрим множества Жюлиа для квадратичных функций комплексной переменной f(z)=z²+c, где с - произвольный параметр.

При фиксированном 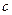(отличном от нуля) в зависимости от выбора начальной точки пределом последовательности 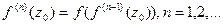будут точки, называемые точками притяжения.

Данные точки, являющиеся пределами последовательностей 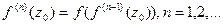в зависимости от выбора параметра 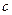функции , называют аттракторами.

Граница, которая разделяет точки притяжения аттрактора 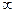, и является множеством Жюлиа.

Заполняющие множества Жюлиа, граница которых являлась множествами Жюлиа, можно построить как с помощью компьютерных программ, написанных на языках программирования высокого уровня, так и с помощью математических пакетов, например, в среде Mathcad.

Множество Жюлиа для f(z) симметрично относительно горизонтальной оси. При написании программы это обстоятельство можно использовать для уменьшения объема вычислений, то есть вычислить множество Жюлиа в верхней полуплоскости, а затем отразить его на нижнюю полуплоскость. Однако обычно это не делается с целью оставить возможность отображения множества на весь экран в различных масштабах.

Построение множество Жюлиа в Mathcad

Пусть мы имеем комплексное число .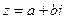

Найдем вещественную и мнимую часть числа .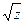

Предположим, что .

Тогда получим систему уравнений:.

Далее имеем: .

Решая данное уравнение, находим:

, .

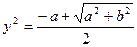Из полученных равенств вытекает, что

(*), (**).

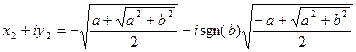Теперь рассмотрим отображение . Для того, чтобы применить определение с) множества Жюлиа, данного в теореме 1, определим точку комплексной области, которая принадлежит образу .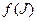

Найдем неподвижную точку для отображения .

.

Положим .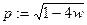

Покажем, что точки и 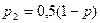являются неподвижными точками отображения .

Имеем: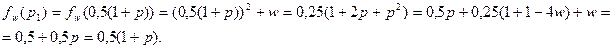

Аналогично находим, что

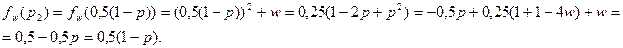
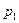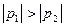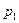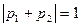Выберем из двух комплексных чисел и то, модуль которого больше. Не нарушая общности рассуждений, будем считать, что . Докажем, что точка будет отталкивающей точкой. Предположим противное. Тогда . Замечаем, что при нашем предположении . Очевидно, что . Однако в силу нашего предположения 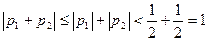. Мы пришли к противоречию.

Таким образом, 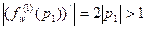. Согласно свойству дифференцирования сложной функции замечаем, что .

Используя метод математической индукции нетрудно показать, что . Таким образом, точка 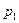- отталкивающая неподвижная точка отображения. Согласно теореме 1 .

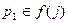Предположим теперь, что . Пусть 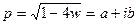, где вещественную часть 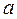и мнимую часть можно найти с помощью формул (*) или (**). Тогда . . 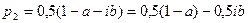Согласно нашему предположению . Из последнего равенства находим, что . Таким образом, , .

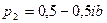Пусть сначала . Поскольку , то 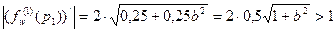. Аналогично находим, что . Таким образом, в данном случае обе точк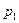и и отталкивающие неподвижные точки.

Рассмотрим теперь случай, когда . Тогда , 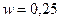и обе точки будут принадлежать образу 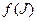. Соответствующее параметру w = 0,25 множество Жюлиа изображено на (рис 8).

Чтобы показать наглядность и красоту фракталов построенных с помощью множества Жюлиа мы будем использовать математический пакет Mathcad, исходя из характеристического свойства 3, приведенного в теореме1.

Алгоритм построения множеств Жюлиа:

1) (задаются числа +1 и -1);

2) 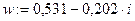(данному w соответствует) 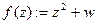(указывается функция, с помощью которой организуется процесс итерирования);

3) 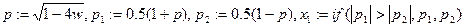. (вычисление отталкивающей периодической точки);

4) , где 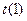принимает значения +1 или -1(с помощью итерирования функции строятся множества Жюлиа. При итерировании функции 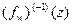в зависимости от значения функции перед корнем берется знак + или -.

Для функции где W = 0.25

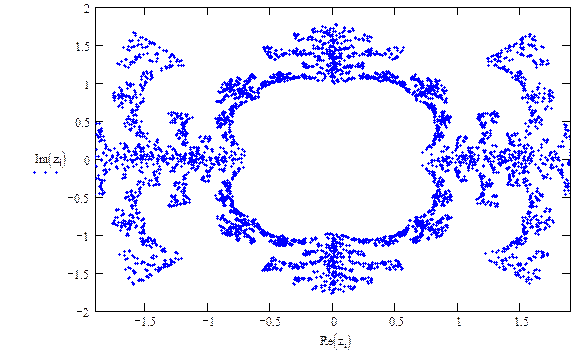
Рис.1

Дата добавления: 2014-01-20