Выборочный коэффициент детерминации

Выборочный множественный коэффициент детерминации показывает качество подгонки регрессионной модели к эмпирическим значениям 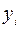и определяется выражением (в отличие от случая модели парной регрессии он обозначается )

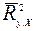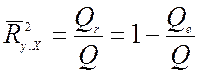(25)

Свойства коэффициента :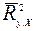

1) Коэффициент 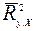служит для оценки значимости (качества) уравнения регрессии, является одной из наиболее эффективных оценок адекватности регрессионной модели, характеристикой её прогностической силы.

2) Коэффициент 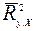при выполнении 5-го условия КЛММР является состоятельной, но смещённой оценкой генерального коэффициента детерминации 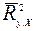, с математическим ожиданием и дисперсией, приближённо определяемыми выражениями

;

.

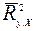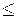
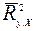
3) Коэффициент - безразмерная величина, лежащая в пределах 0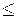1.

4) При 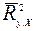=0 вариация зависимой переменной полностью обусловлена воздействием неучтённых в модели переменных и линия регрессии не улучшает качество предсказания значений 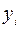по сравнению с тривиальным предсказанием

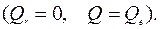
5) При 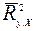=1 осуществляется точная подгонка и все эмпирические точки 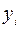удовлетворяют уравнению регрессии

6) Коэффициент 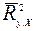может быть вычислен из матрицы парных коэффициентов корреляции по формуле

(26)

где - определитель симметричной квадратной матрицы выборочных парных коэффициентов корреляции - го порядка

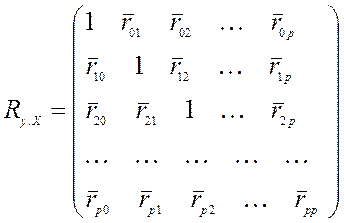(27)

с элементами

(28)

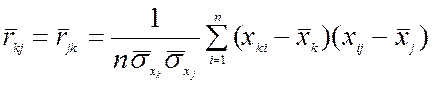(29)

где 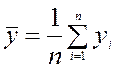; ; 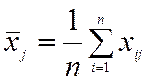- алгебраическое дополнение 0 – го элемента 0 – й строки матрицы (27), по сути представляющее собой определитель матрицы межфакторной парной корреляции р – го порядка

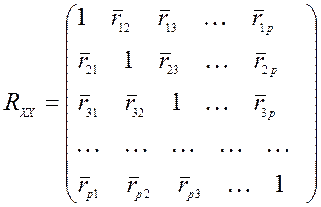(30)

Выражение (26) определяет выборочный множественный коэффициент детерминации р – го порядка (по числу р объединяющих переменных). Множественные коэффициенты детерминации низших порядков определяются аналогичным образом из соответствующих подматриц матриц .

Так, выборочный множественный коэффициент детерминации 1 – го порядка 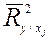, равный квадрату парного коэффициента корреляции между результирующе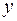й и 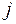- ой объясняющей переменной , находятся по формуле

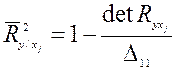(31)

где - определитель подматрицы 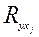, получаемый из матрицы путём вычёркивания всех строк и столбцов кроме тех, которые соответствуют переменным 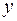и (первые 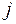- е строка и столбец);

- алгебраическое дополнение 1 – го элемента 1 – й строки этой подматрицы.

Выборочный множественный коэффициент детерминации 2 – го порядка 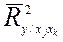для объясняемой 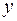и факторных переменных , определяется выражением

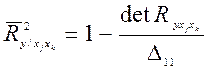(32)

где - определитель подматрицы , которая находится из матрицы 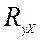в результате вычёркивания всех строк и столбцов кроме тех, которые отвечают 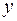,и ; 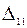- алгебраическое дополнение 1 – го элемента 1 – й строки полученной подматрицы.

Выборочные множественные коэффициенты детерминации более высоких порядков находятся аналогичным образом.

7) Величина 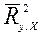, вообще говоря, возрастает при добавлении новых регрессоров (поскольку растёт ), хотя это не обязательно означает улучшение качества регрессионной модели.

Поскольку присоединение в уравнение регрессии каждой новой предикторной переменной не может уменьшить величины коэффициента детерминации (независимо от порядка присоединения), множественные коэффициенты детерминации различных порядков удовлетворяют цепочке неравенств

(33)

Попытка устранить эффект, связанный с ростом 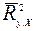при добавлении новых объясняющих переменных, является коррекция 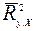на число регрессоров.

Дата добавления: 2014-01-20