Поступательное движение

Основные кинематические характеристики движения:

для точки – ее скорость и ускорение;

для твердого тела - скорость и ускорение поступательного движения и угловая скорость и угловое ускорение вращательного движения.

Опр. 1.1.9. Скорость – величина, показывающая быстроту и направление движения тела; бывает:

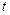· Вектором средней скорости в промежутке времени от до 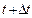называется отношение приращение 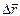радиус – вектора точки за этот промежуток времени к его продолжительности 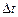: 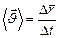(1.1.2)

Средняя скорость – скалярная величина, равная отношению длины пути, пройденного за промежуток времени от 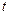до 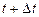, к длительности этого промежутка времени 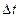: 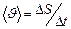. (1.1.2’)

Характеризует движение в течение всего промежутка времени .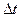

· Скорость (мгновенная скорость, скорость в данный момент времени) - векторная величина, равная первой производной по времени от радиус-вектора движущейся точки: 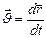. (1.1.3)

Вектор скорости направлен по касательной к траектории в сторону движения точки. Из формулы (1.1.1) следует, что 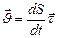и модуль скорости численно равен первой производной от длины пути по времени 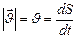. (1.1.3’)

При равномерном движении (численное значение скорости не зависит от времен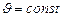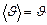и, ): и .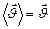

Размерность скорости: .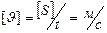

Замечание 1.1.1. Если известно значение вектора скорости 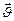, то по формуле (1.1.3) элементарное перемещение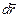точки найдем как 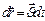. Интегрируя правую и левую части равенства, получим: 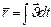. (1.1.4)

По формуле (1.1.3’) аналогично находим 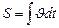. (1.1.5)

Замечание 1.1.2. В общем случае скорость является функцией времени и формулы (1.1.4) и (1.1.5.) следует записывать таким образом: 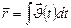и 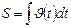. Поэтому при нахождении пути и перемещения необходимо знать характер временной зависимости скорости.

Опр. 1.1.10. Ускорение:

· Средним ускорением в промежутке времени от 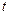до 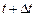называется вектор 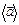, равный отношению приращения 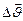скорости 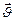точки за этот промежуток времени к его продолжительности 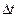: 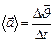(1.1.6)

· Ускорение (мгновенное ускорение) наз. векторная величина, характеризующая быстроту изменения скорости движущейся точки и равная первой производной по времени от скорост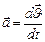и или 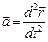(1.1.7)

Вектор ускорения лежит в соприкасающейся плоскости, проходящей через главную нормаль и касательную к траектории, и направлен в сторону вогнутости траектории. Частные случаи:

при прямолинейном движении по прямой вдоль траектории движения;

при равнозамедленном движении противоположно направлению скорости,

при равноускоренном движении совпадает с направлением скорости;

при свободном падении вертикально вниз и неизменен по модулю .

Замечание 1.1.3. Если известно значение вектора ускорения 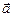, то по формуле (1.1.7) получим: 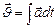. (1.1.8)

С учетом замечания 2: 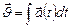. (1.1.8’)

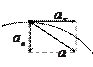Размерность ускорения: .

Рис. 1.1.3

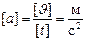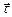Т.к. при движении по некоторой траектории в соприкасающейся плоскости (где лежит вектор ускорения) есть два избранных направления - касательной к траектории (орт ) и главной нормали (орт 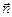), то для нахождения мгновенного ускорения 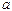его удобно разложить на две взаимно перпендикулярные составляющие по базису 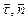: 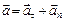, где 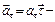танген­циальное (касательное) ускорение, и 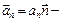нормальное (центростремительное) ускоре­ние.

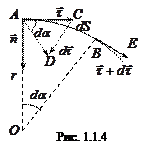Т.к. скорость точки (по 1.1.3’) 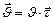, то .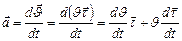

Чтобы проанализировать полученное соотношение, разобьем траекторию движения точки на столь малые участки, что каждый из них можно считать участком окружности радиуса 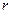с центром в т. О.

Опр. 1.1.11. Величину 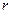называют радиусом кривизны траектории – радиус окружности, совпадающей с траекторией в окрестности данной точки.

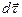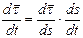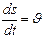Приращение орта касательной к траектории , но , а 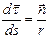. В результате получаем 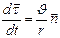. Тогда выражение для ускорения примет вид .

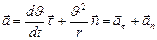Тангенциальное ускорение характеризует быстроту изменения скорости по величине, направлено вдоль касательной к траектории и выражается формулой 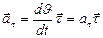, где (1.1.9)

Нормальное ускорение характеризует быстроту изменения скорости по направлению, направлено вдоль главной нормали (к центру кривизны траектории) и выражается формулой 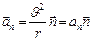, где 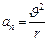, (1.1.10)

Полное ускорение (модуль ускорения) 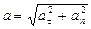, (1.1.11)

При втором способе описания движения (когда даются уравнения, выражающие зависимость координат точки от времени: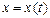;;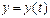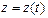), уравнение траектории находится путем исключения времени из данных уравнений. Проекции скорости на оси координат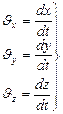и ускорения 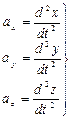(1.1.12)

Модули векторов скорости и ускорения выражаются через проекции: 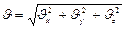; 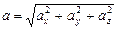. (1.1.13)

Вектора скорости и ускорения можно разложить по базису 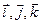: 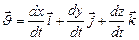; 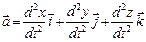. (1.1.14)

По характеру изменения скорости различают:

1. Если модуль мгновенной скорости с течением времени не изменяется 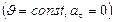, то движение материальной точки называется равномерным. Т.о. точка проходит за равные промежутки времени пути равной длины и по формуле (1.1.5.) 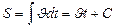. Постоянная интегрирования 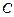определяется из условия 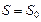при 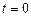, откуда получаем 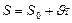- уравнение равномерного движения.

2. Если модуль мгновенной скорости с течением времени изменяется 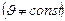, то движение материальной точки называется неравномерным (переменным). Движение, при котором 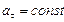называется равнопеременным, а именно, если ускорение 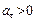, то движение равноускоренное и направления векторов 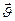и 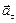совпадают, если 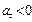, то движение равнозамедленное и направления векторов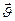и 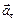противоположны.

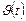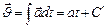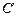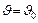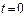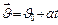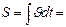
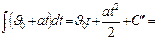
Для нахождения уравнения движения в данном случае, прежде чем воспользоваться формулой (1.1.5) мы, учитывая замечание 1.1.2, должны установить характер зависимости . Т.к. ускорение при равнопеременном движении от времени не зависит, то по формуле (1.1.8) . Постоянная интегрирования определяется из условия при , откуда получаем . Теперь по формуле (1.1.5) 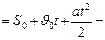уравнение равнопеременного движения.

Пусть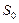 — расстояние движущейся точки от начала координат в момент времени 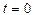; 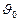— скорость точки в момент времени .

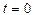	Равномерное движение	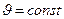Неравномерное движение ,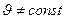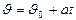
Прямолинейное движение	ускорение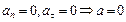
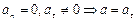
уравнение движения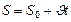
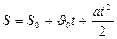
Криволинейное движение
ускорение

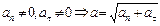
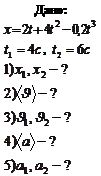Пример 1.1.1. Уравнение движения точки по прямой имеет вид 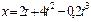. Найти: 1)положе­ния точки в моменты времен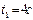и и 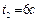; 2)среднюю скорость за время между этими моментами; 3)мгновенные скорости в указанные моменты времени; 4) среднее ускорение за указанный промежуток времени; 5) мгновенные ускорения в указанные моменты времени.

Решение:

1) Положение точки, движущейся по прямой, можно найти, подставив в уравнение движения заданное значение времени:

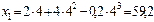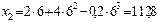м,м.

2) Средняя скорость: .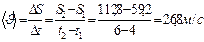

3) Мгновенная скорость: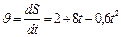. Подставим значения времени и получим: , .

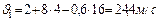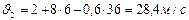4) Среднее ускорение: .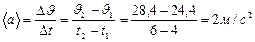

5) Мгновенное ускорение: 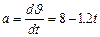. Подставим значения времени: , .

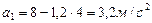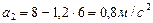Пример 1.1.2. Машина идет по закругленному шоссе с ускорением 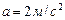. Уравнение движения автомобиля 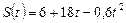. Найти скорость машины, ее тангенциальное и нормальное ускорение в момент времени 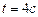, а также радиус кривизны шоссе.

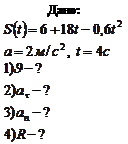Решение:

По определению мгновенной скорости .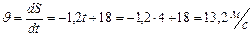

По определению 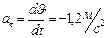- тангенциальное ускорение постоянно по величине, т.е. движение машины равнозамедленное. Полное ускорение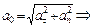 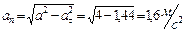. Т.к.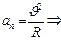 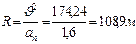-радиус кривизны траектории в момент времени 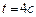. Направление полного ускорения можно определить как угол, образуемый полным ускорением с направлением нормального ускорения .

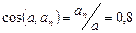Дата добавления: 2014-01-11